Operations on Spherical Functions

The idea of variables of type S2Fun is to calculate with spherical functions similarly as Matlab does with vectors and matrices. In order to illustrate this we consider the following two spherical functions

sF1 = S2Fun.smiley;
sF2 = S2FunHarmonic.unimodal('halfwidth',10*degree)

plotx2north
plot(sF1,'upper')
nextAxis
plot(sF2,'upper')

sF2 = S2FunHarmonic
  bandwidth: 50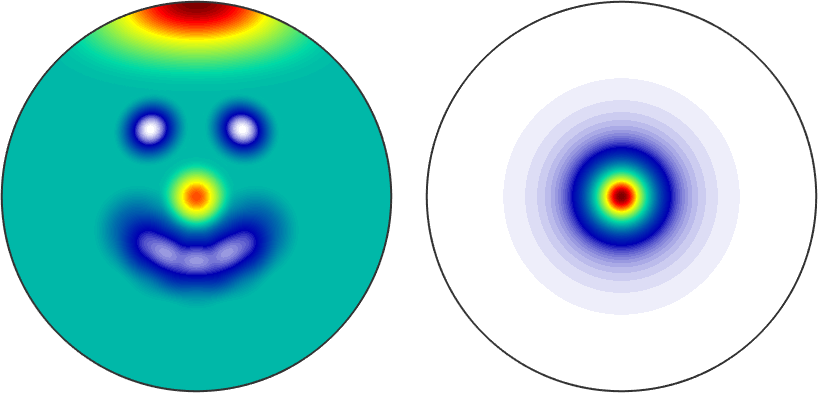
  isReal: true

Basic arithmetic operations

Now the sum of these two spherical functions is again a spherical function

1 + 15 * sF1 + sF2

plot(15 * sF1 + sF2,'upper')

ans = S2FunHarmonic
  bandwidth: 128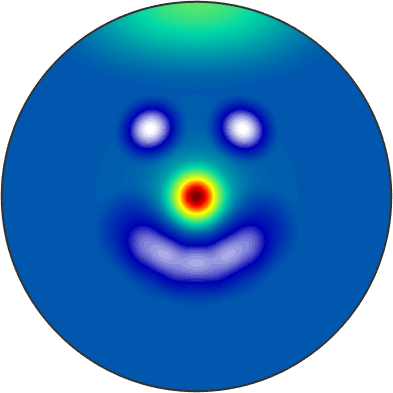
  isReal: true

Accordingly, one can use all basic operations like -, *, ^, /, min, max, abs, sqrt to calculate with variables of type S2Fun.

% the maximum between two functions
plot(max(15*sF1,sF2),'upper');

nextAxis
% the minimum between two functions
plot(min(15*sF1,sF2),'upper');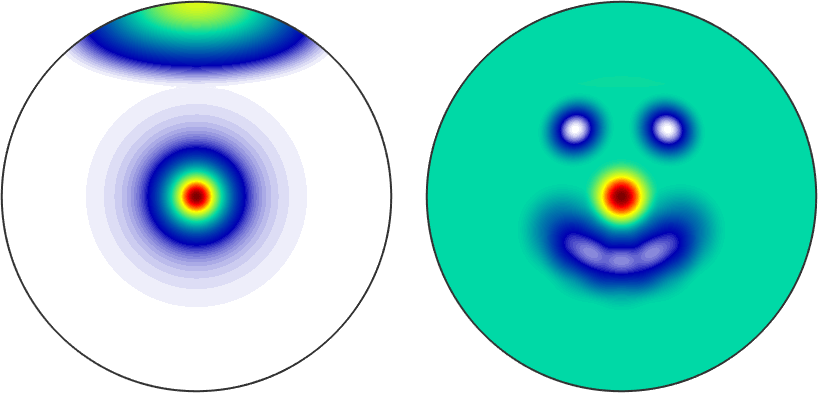

Local Extrema

The above mentioned functions min and max have very different use cases

plot(15 * sF1 + sF2,'upper')

% compute and mark the global maximum
[maxvalue, maxnodes] = max(15 * sF1 + sF2);
annotate(maxnodes)

% compute and mark the local minimum
[minvalue, minnodes] = min(15 * sF1 + sF2,'numLocal',2);
annotate(minnodes)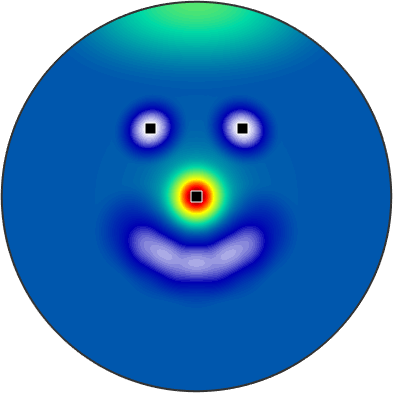

Integration

The surface integral of a spherical function can be computed by either mean or sum. The difference between both commands is that sum normalizes the integral of the identical function on the sphere to \(4 \pi\), the command mean normalizes it to one. Compare

mean(sF1)

sum(sF1) / ( 4 * pi )

ans =
    0.0064
ans =
    0.0064

A practical application of integration is the computation of the \(L^2\)-norm which is defined for a spherical function \(f\) by

\[ \| f \|_2 = \left(\int_{\mathrm{sphere}} \lvert f(\xi)\rvert^2 \,\mathrm d\xi\right)^{1/2} \]

accordingly we can compute it by

sqrt(sum(sF1.^2))

ans =
    0.4229

or more efficiently by the command norm

norm(sF1)

ans =
    0.4229

Differentiation

The differential of a spherical function in a specific point is a gradient, i.e., a three-dimensional vector which can be computed by the command grad

grad(sF1,xvector)

ans = vector3d
  x           y           z
  0 3.00208e-06 0.000366047

The gradients of a spherical function in all points form a spherical vector field and are returned by the function grad as a variable of type S2VectorFieldHarmonic.

% compute the gradient as a vector field
G = grad(sF1)

% plot the gradient on top of the function
plot(sF1,'upper')
hold on
plot(G)
hold off

G = S2VectorFieldHarmonic
 bandwidth: 129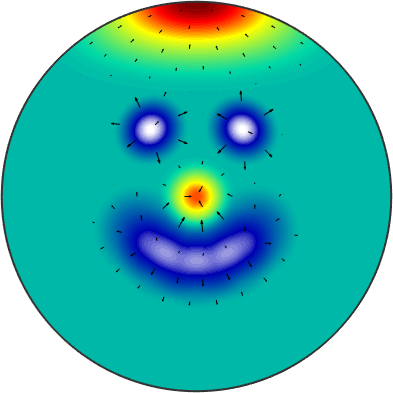

We observe long arrows at the positions of big changes in intensity and almost invisible arrows in regions of constant intensity.

Rotating spherical functions

Rotating a spherical function works with the command rotate

% define a rotation
rot = rotation.byAxisAngle(yvector,-30*degree)

% plot the rotated spherical function
plot(rotate(15 * sF1 + sF2,rot),'upper')

rot = rotation
 
  Bunge Euler angles in degree
  phi1  Phi phi2
   270   30   90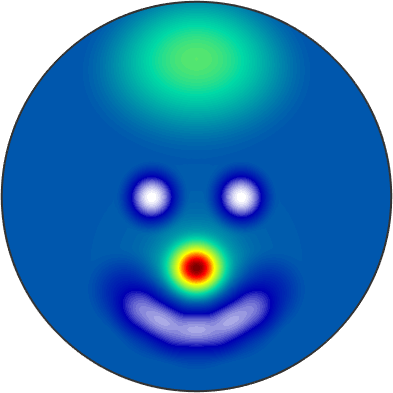

A special case of rotation is symmetrising it with respect to some symmetry. The following example symmetrises our smiley with respect to a two fold axis in \(z\)-direction

% define the symmetry
cs = crystalSymmetry('112');

% compute the symmetrised function
sFs = symmetrise(sF1, cs)

% plot it
plot(sFs,'upper','complete')

sFs = S2FunHarmonicSym (112)
  bandwidth: 128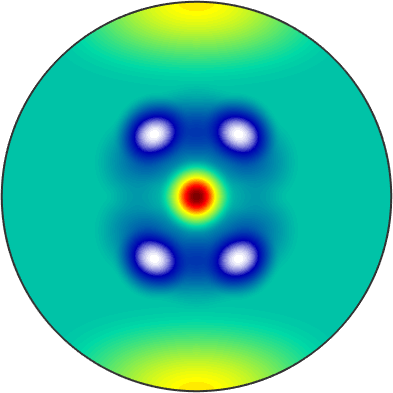
  isReal: true

The resulting function is of type S2FunHarmonicSym and knows about its symmetry.