S2AxisFieldHarmonic

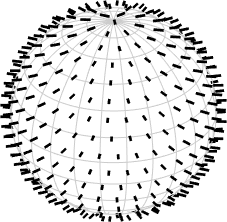
The class @S2AxisFieldharmonic handles axis fields on the sphere, i.e. spherical functions

\[ f\colon {\bf S}^2\to{\bf R}^3_{/<\pm \mathrm{Id}>}. \]

that associates to each point \(\xi\) on the sphere a three dimensional vector \(\vec v = f(\xi)\) where we do not distinguish between \(-\vec v\) and \(\vec v\). A typical example would be the polarization direction.

Defining a S2AxisFieldHarmonic

Definition via function values

At first you need some vertices

nodes = equispacedS2Grid('points', 1e5);
nodes = nodes(:);

Next you define function values for the vertices

y = vector3d(sin(5*nodes.x), 1, nodes.y, 'antipodal');

Now the actual command to get sAF1 of type S2AxisFieldHarmonic

sAF1 = S2AxisFieldHarmonic.interpolate(nodes, y)

plot(sAF1)

sAF1 = S2AxisFieldHarmonic
 bandwidth: 224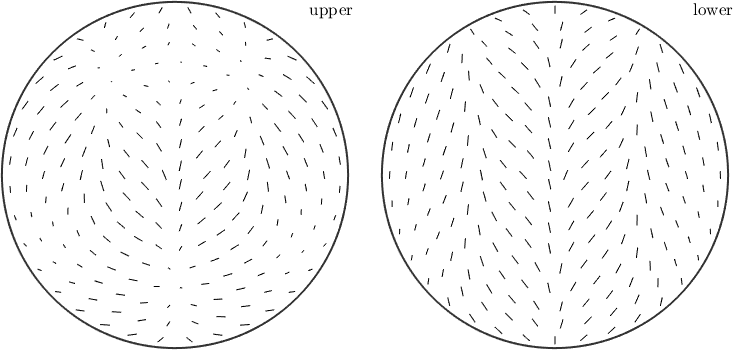

Definition via function handle

If you have a function handle for the function you could create a S2AxisFieldHarmonic via quadrature. At first lets define a function handle which takes vector3d as an argument and returns antipodal vector3d:

f = @(v) vector3d(v.x, v.y, 0*v.x, 'antipodal');

Now you can call the quadrature command to get sAF2 of type S2AxisFieldHarmonic

sAF2 = S2AxisFieldHarmonic(@(v) f(v))
% sAF2 = S2AxisFieldHarmonic.quadrature(@(v) f(v))

clf;
quiver3(sAF2);

sAF2 = S2AxisFieldHarmonic
 bandwidth: 128