Assume an arbitrary ODF either from texture modelling or recovered from XRD pole figure measurements a common problem is the simulation of random individual orientations that are distributed according the given ODF. This is helpful crucial in many application, e.g., for running plastic deformation models like VPSC or verifying the accuracy density estimation methods. Here we start with a trigonal alpha-fibre ODF which we define by
cs = crystalSymmetry('32');
fibre_odf = 0.5*uniformODF(cs) + 0.5*fibreODF(fibre.rand(cs),'halfwidth',20*degree);
plot(fibre_odf,'sections',6,'silent')
mtexColorbar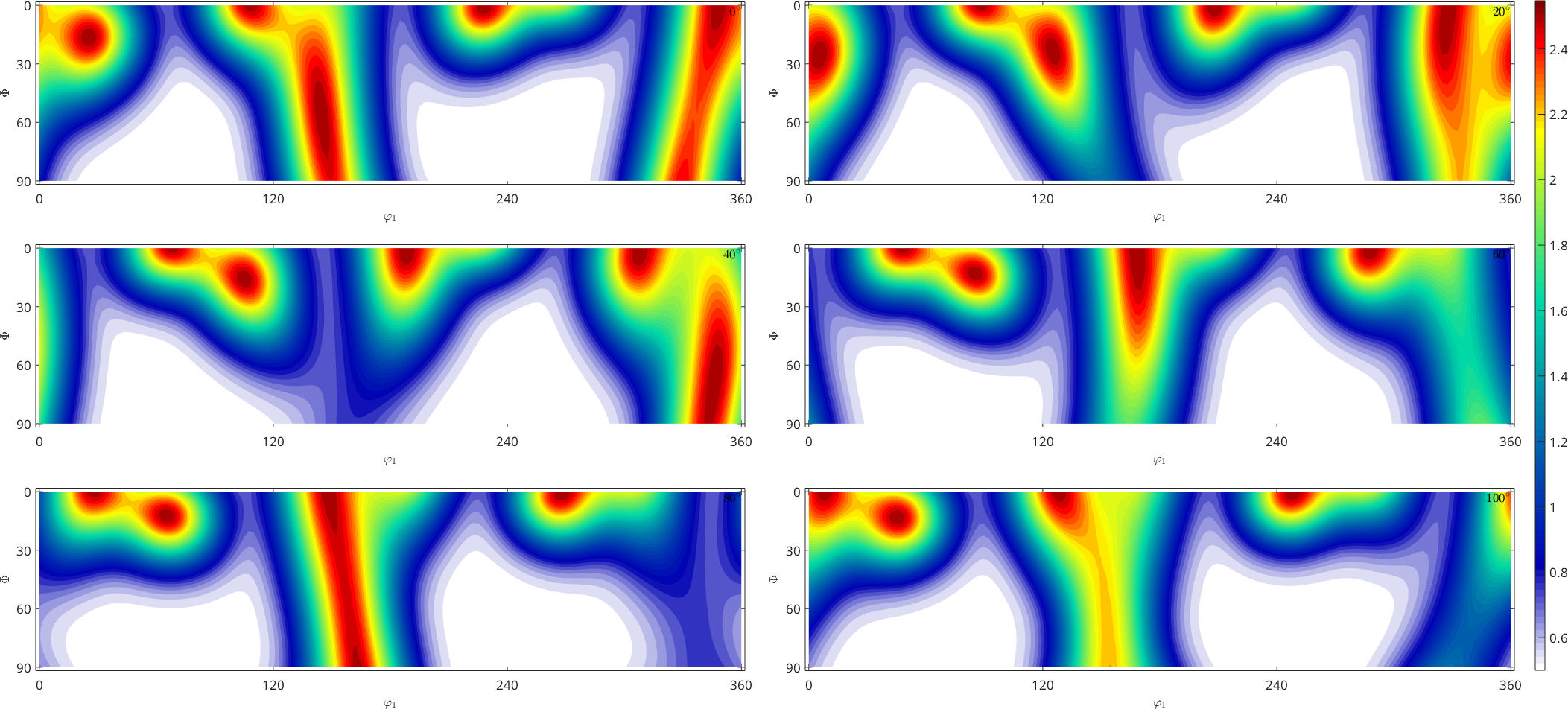
Computing Random Orientations
In order to compute \(50000\) random orientation from the ODF fibre_odf we use the command discreteSample.
ori = fibre_odf.discreteSample(50000)
% plot the orientations into the Bunge sections
hold on
plot(ori,'MarkerFaceColor','none','MarkerEdgeAlpha',0.5,'all','MarkerEdgeColor','k','MarkerSize',4)
hold offori = orientation (321 → y↑→x)
size: 50000 x 1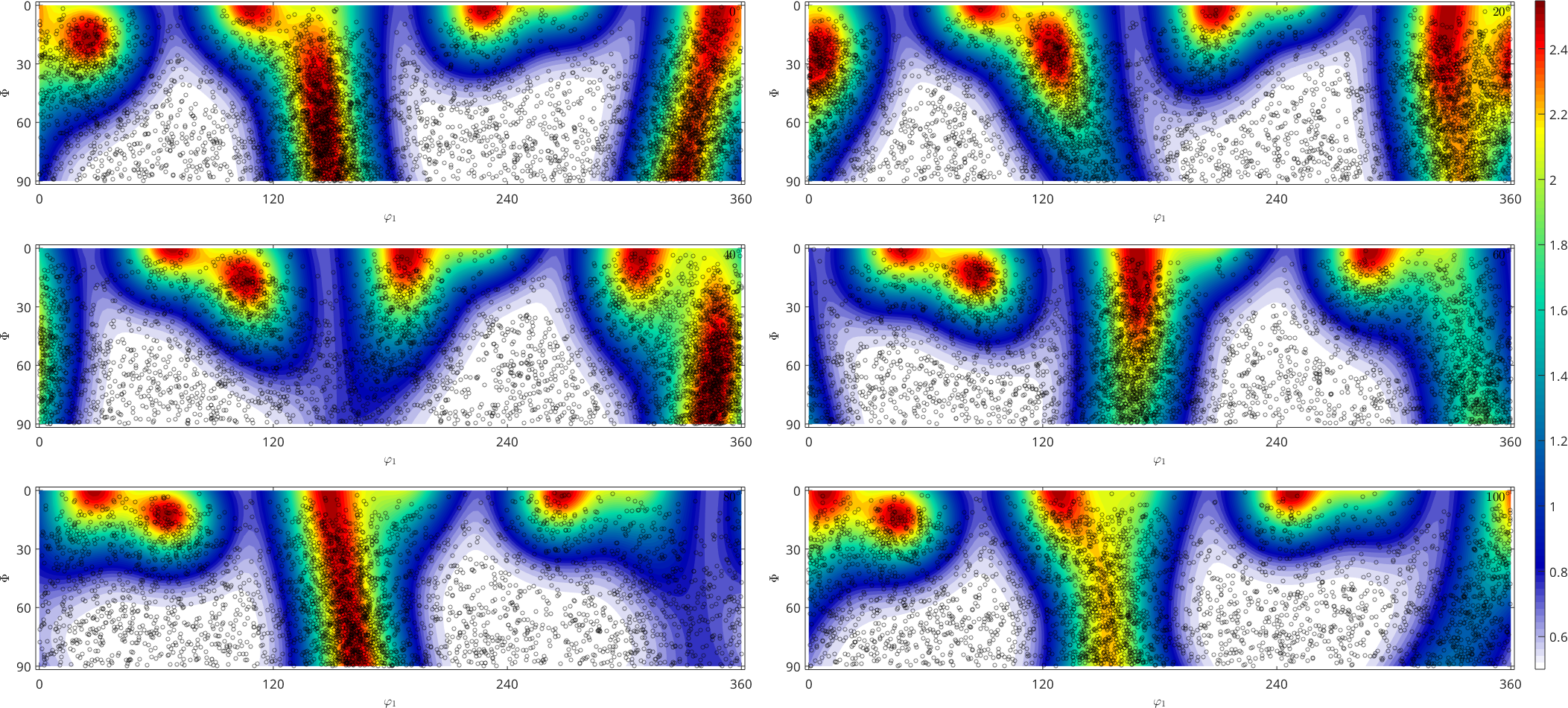
From the above plot it is very hard to judge whether the orientations are indeed distributed according to the given ODF. The reason for this is the not volume preserving projection of the Bunge sections. A better ODF representation for this purpose are sigma sections
% plot the ODF in sigma sections
plot(fibre_odf,'sections',6,'silent','sigma','contour','linewidth',2)
% plot the orientations into the sigma sections
hold on
plot(ori,'MarkerFaceColor','none','MarkerEdgeAlpha',0.25,'all','MarkerEdgeColor','k','MarkerSize',4)
hold off
ODF Estimation from Random Orientations
From the last plot we clearly see that the orientations are more dense close to the alpha fibre. In order more quantitative measure for how well do the orientations approximate the ODF we may use the orientations to estimate a new ODF and compare the fit of this estimate ODF with the initial ODF.
% estimate an ODF from the random orientations
odf_rec = calcDensity(ori)
% plot the estimated ODF
plot(odf_rec,'sections',6,'silent')odf_rec = SO3FunHarmonic (321 → y↑→x)
bandwidth: 25
weight: 1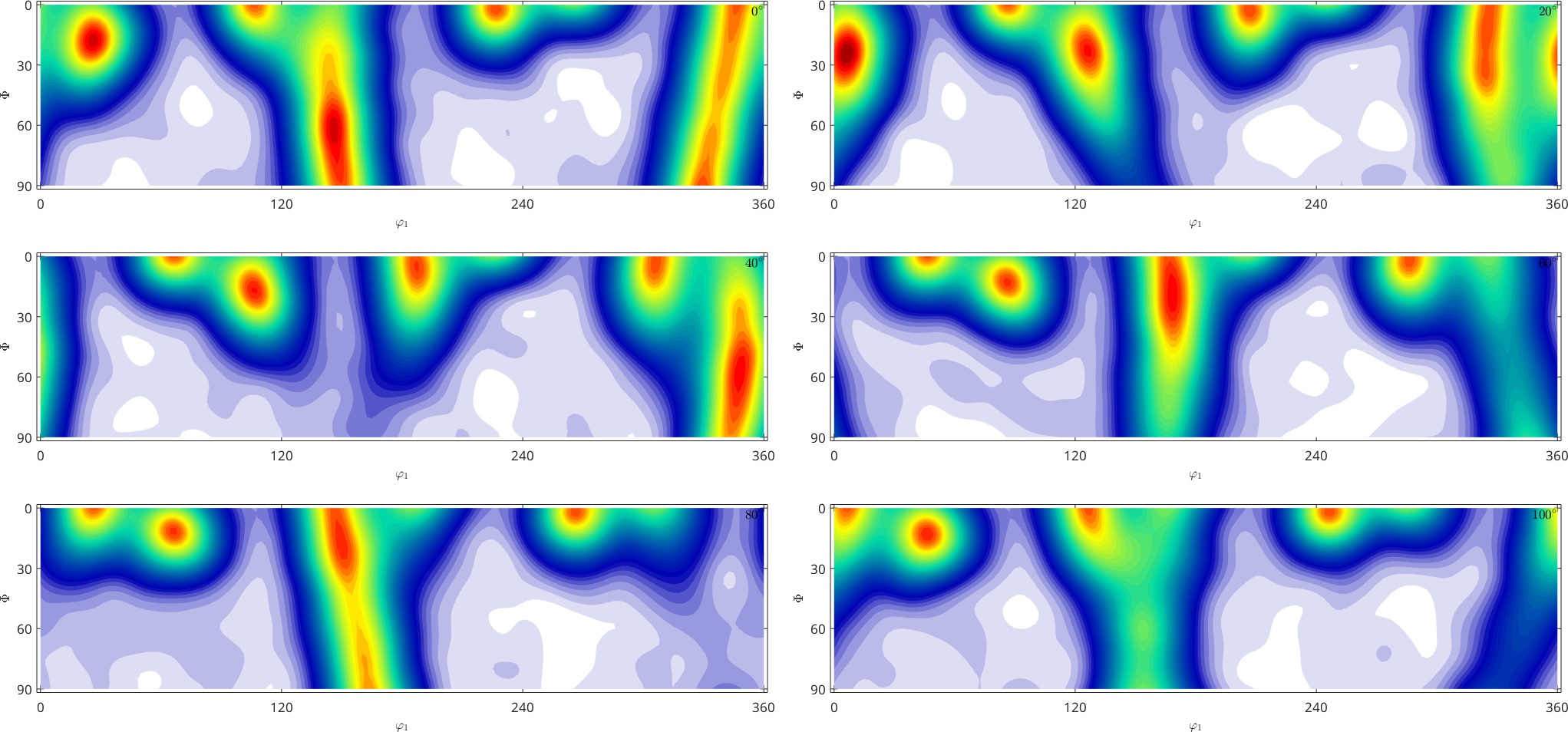
We may now compare the original model ODF fibre_odf with the reconstructed ODF odf_rec.
calcError(odf_rec,fibre_odf)ans =
0.0501Exporting Random Orientations
In order to make use of the sampled orientations you probably want to export them as Euler angles into a text files. This can be done using the commands export and export_VPSC.