Orientation Dependent Functions

An orientation dependent function is a function that assigns to each rotation or orientation a numerical value. An import example of a rotational function is the orientation density function (ODF) that assigns to each crystal orientation the probability of its occurrence within a specimen. Other examples are the Schmidt or the Taylor factor as a function of the crystal orientation.

Definition of a orientation dependent function

Within MTEX a rotational function is represented by a variable of type SO3Fun. Let us consider as an example the function that takes an orientation and returns it rotational angle modulo cubic crystal symmetry. In MTEX the rotational angle is computed by the command angle(ori). In order to turn this correspondence into a SO3Fun we use the command SO3FunHandle and pass the angle command as an anonymous function.

% define the crystal symmetry
cs = crystalSymmetry('432');

% construct the SO3Fun
SO3F = SO3FunHandle(@(ori) angle(ori) ./ degree, cs)

SO3F = SO3FunHandle (432 → y↑→x)
  eval: @(ori)angle(ori)./degree

Many more methods for defining orientation dependent functions are discussed here.

The entire information about the orientation dependent function is now stored in the variable SO3F. In order to determine its value for a specific orientation ori the function eval(ori) is used.

ori = orientation.rand(cs)
SO3F.eval(ori)

ori = orientation (432 → y↑→x)
 
  Bunge Euler angles in degree
     phi1     Phi    phi2
  156.958 161.468 197.878
 
ans =
   44.7566

Plotting an orientation Dependent Function

Orientation dependent functions are most often visualized by sections according to the third Euler angle \(\varphi_2\).

plotSection(SO3F)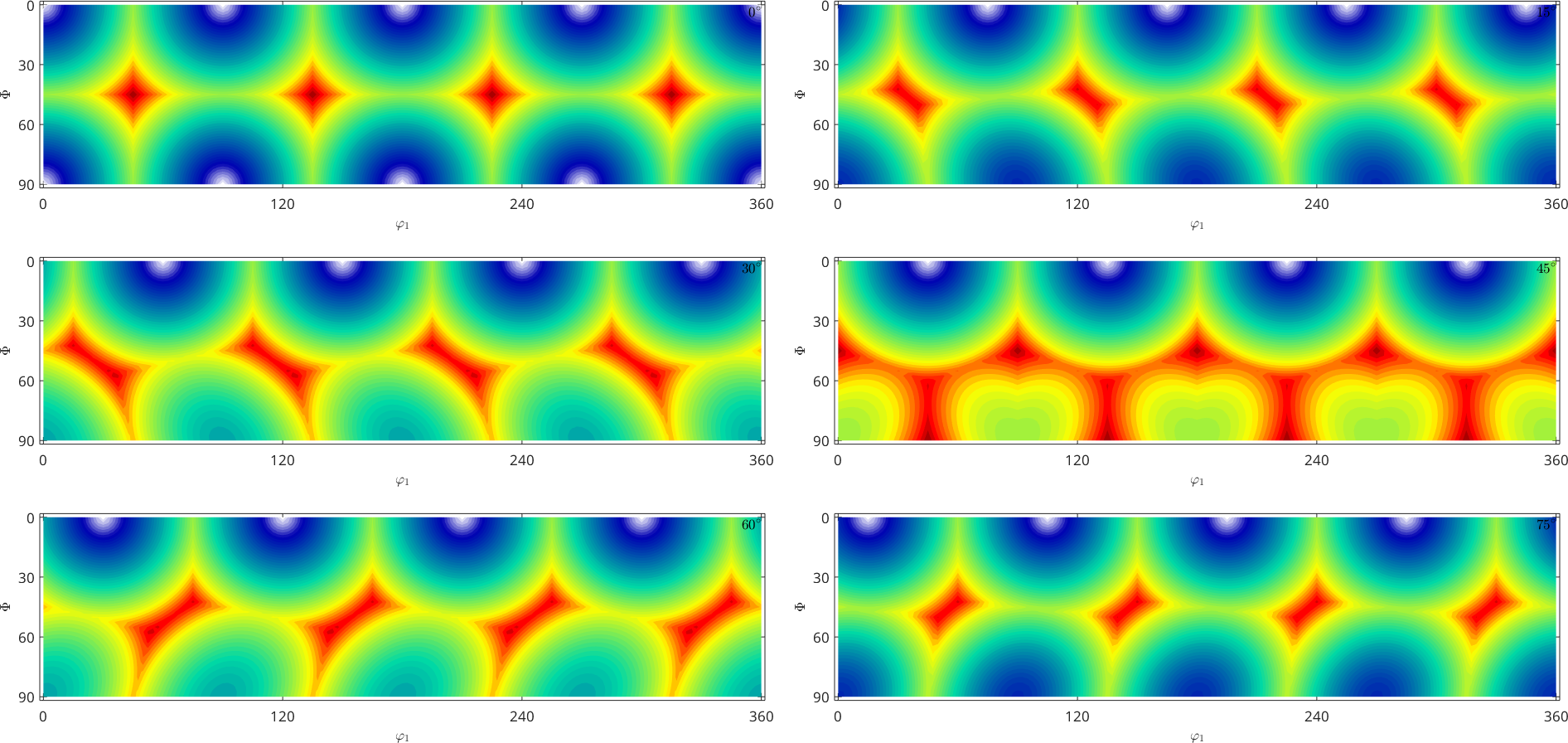

The plot tells us for which Euler angles the resulting rotational angle is large and for which Euler angles it is low. The plot of this "angle function" SO3F becomes trivial if represented in an axis angle sections

plotSection(SO3F,'axisAngle','upper')
mtexColorbar
mtexColorMap parula

Warning: Contour not rendered for constant ZData 
Warning: Contour not rendered for constant ZData 
Warning: Contour not rendered for constant ZData 
Warning: Contour not rendered for constant ZData 
Warning: Contour not rendered for constant ZData

as obviously, the function value is constant in each section. Many more methods for visualizing orientation dependent functions are discussed here.

Computing with orientation dependent functions

The power of representing an orientation dependent functions as a variables of type SO3Fun is that we may apply to it a large number of analysis tools. In particular, one can add, subtract and multiply orientation dependent functions, plot them in various projections or detect the local minima or maxima. In the case of our example function the local maxima refers to the orientations with maximum rotational angle in cubic symmetry. We may compute them by the command max.

[value,ori] = max(SO3F,'numLocal',10,'accuracy',0.001*degree)

value =
   62.7993
   62.7993
   62.7993
   62.7993
   62.7993
   62.7993
 
ori = orientation (432 → y↑→x)
  size: 6 x 1
 
  Bunge Euler angles in degree
         phi1         Phi        phi2
          135          45         180
      270.001     44.9999     44.9994
      54.7356          60     324.736
      44.9997     44.9999         270
      90.0002     45.0001         225
  0.000124236          45         315

We observe that there are exactly six symmetrically not equivalent orientations that realize an orientation angle of about 62.994 degree and form the vertices of the fundamental region in orientation space

color = ind2color(repmat(1:length(ori),numSym(cs),1));
plot(ori.symmetrise,color,'axisAngle','filled','markerSize',20,'restrict2FundamentalRegion')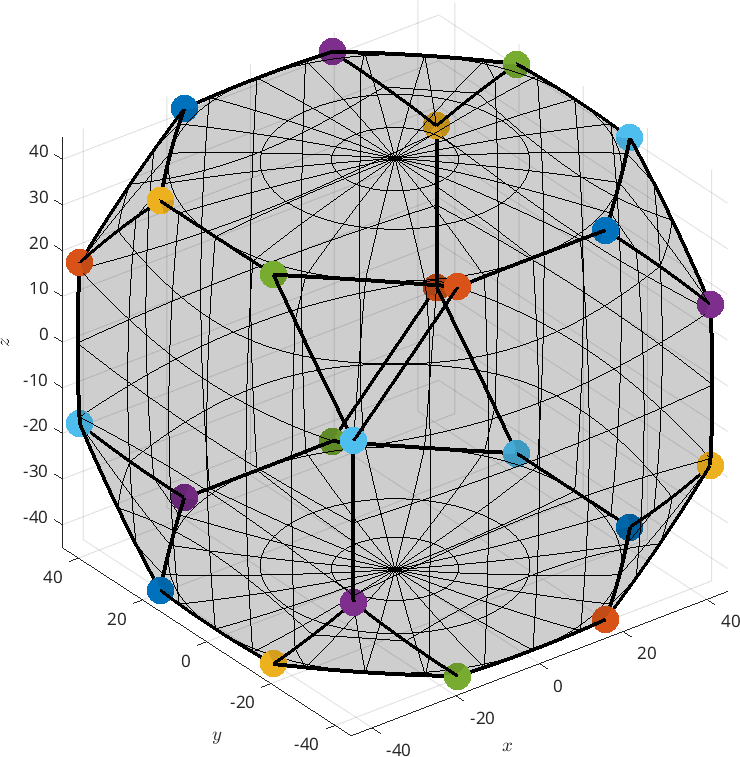

Representations of Rotational Functions

Internally MTEX represents rotational functions in different ways:

All representations allow the same operations which are specified for the abstract class SO3Fun. In particular it is possible to calculate with \(SO(3)\) functions as with ordinary numbers, i.e., you can add, multiply arbitrary functions, take the mean, integrate them or compute gradients, see Operations.

Generalizations of Rotational Functions