During phase transformation or twinning the orientation of a crystal rapidly flips from an initial state oriA into a transformed state oriB. This relationship between the initial and transformed state can be described by an orientation relationship OR. To make the situation more precise, we consider the phase transformation from austenite to ferrite via the Nishiyama Wassermann orientation relationship
% parent and child crystal symmetry
csP = crystalSymmetry('432','mineral','Austenite');
csC = crystalSymmetry('432','mineral','Ferrite');
% the orientation relationship
p2c = orientation.NishiyamaWassermann(csP,csC);Now an arbitrary Austenite orientation
oriA = orientation.rand(csP)oriA = orientation (Austenite → y↑→x)
Bunge Euler angles in degree
phi1 Phi phi2
156.958 161.468 197.878is transformed in one of the following Ferrite orientations
oriB = variants(p2c,oriA)oriB = orientation (Ferrite → y↑→x)
size: 1 x 12
Bunge Euler angles in degree
phi1 Phi phi2
95.6328 91.0043 16.4349
330.335 152.635 96.6679
23.6163 57.205 298.401
311.882 62.194 268.771
186.966 63.9508 170.719
46.1511 49.9141 104.876
183.862 83.1959 351.609
80.4228 132.659 125.129
110.65 31.2299 298.288
54.5999 141.255 286.055
333.585 64.3114 78.9078
89.9532 72.3537 197.269These 12 Ferrite orientations are called variants of the orientation relationship. Lets visualize them in a pole figure plot
hC = Miller({1,1,1},{1,1,0},csC);
hP = Miller({1,1,0},{1,0,0},csP);
% plot the child variants
plotPDF(oriB,hC,'MarkerSize',5,'markerColor','black','figSize','medium');
% and on top the parent orientation
opt = {'MarkerFaceColor','none','MarkerEdgeColor','darkred','linewidth',3};
for k = 1:2
nextAxis(k)
hold on
plot(oriA * hP(k).symmetrise ,opt{:})
xlabel(char(hP(k),'latex'),'Color','red','Interpreter','latex')
hold off
end
drawNow(gcm)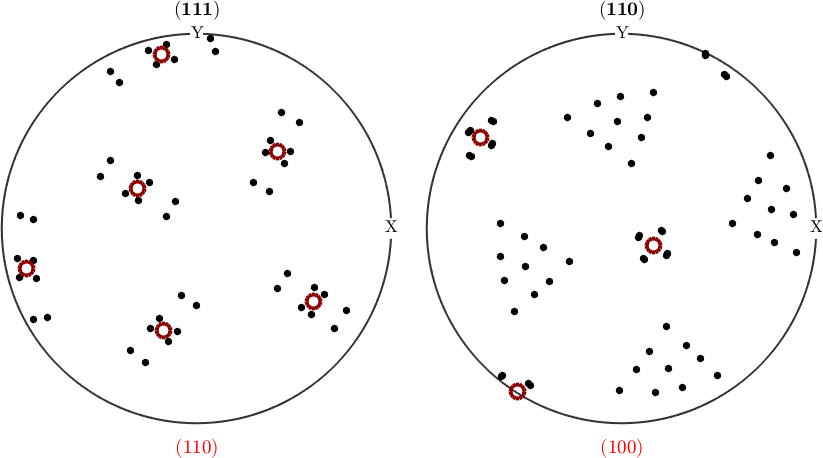
In case we have multiple parent orientations following some initial orientation distribution function odf
% define a model ODF
odfA = unimodalODF(oriA,'halfwidth',5*degree)
plotPDF(odfA,hP,'figSize','medium')
mtexColorbarodfA = SO3FunRBF (Austenite → y↑→x)
unimodal component
kernel: de la Vallee Poussin, halfwidth 5°
center: 1 orientations
Bunge Euler angles in degree
phi1 Phi phi2 weight
156.958 161.468 197.878 1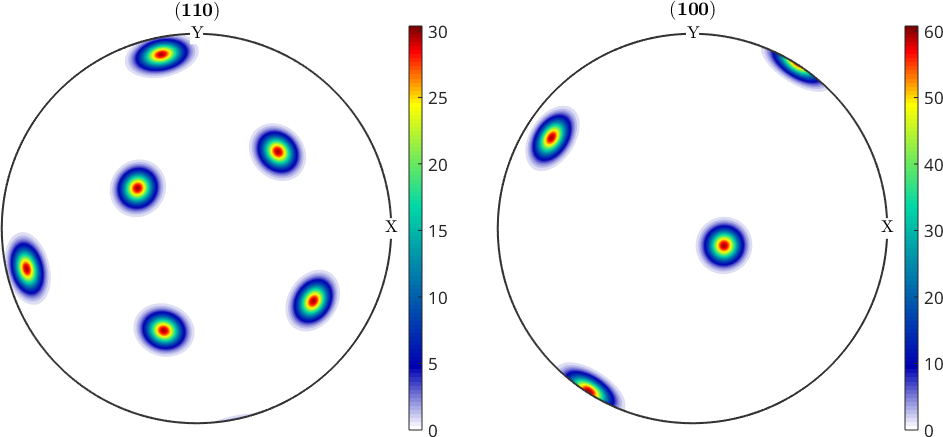
We can draw some random orientations according this model ODF and apply the same commands variants to compute all transformed orientations in one step
% number of discrete orientations
n = 10000;
oriASim = odfA.discreteSample(n)
% transform the orientations
oriBSim = variants(p2c,oriASim)
% show the result
plotPDF(oriBSim,hC,'contourf','figSize','medium');
mtexColorbaroriASim = orientation (Austenite → y↑→x)
size: 10000 x 1
oriBSim = orientation (Ferrite → y↑→x)
size: 10000 x 12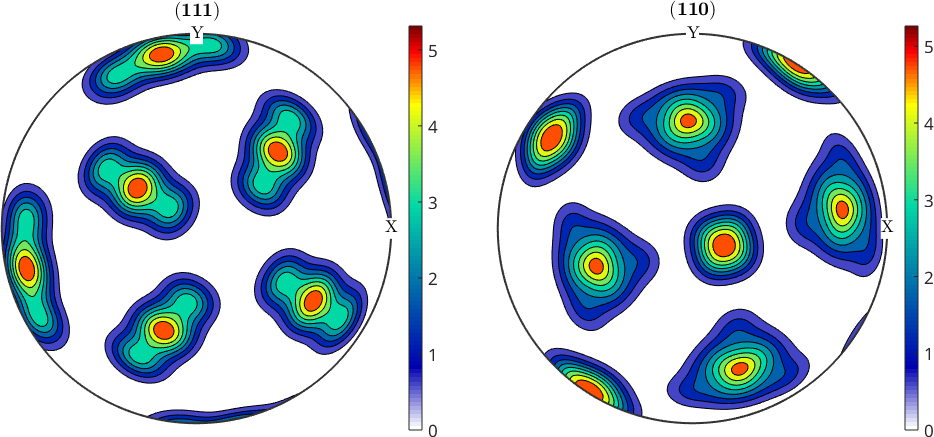
An alternative and better approach is to directly use odfA as an input to the function variants. In this case the output is the orientation distribution function of the transformed material
% compute the child ODF
odfB = variants(p2c,odfA)
% plot
plotPDF(odfB,hC,'contourf','figSize','medium');
mtexColorbarodfB = SO3FunHarmonic (Ferrite → y↑→x)
bandwidth: 48
weight: 1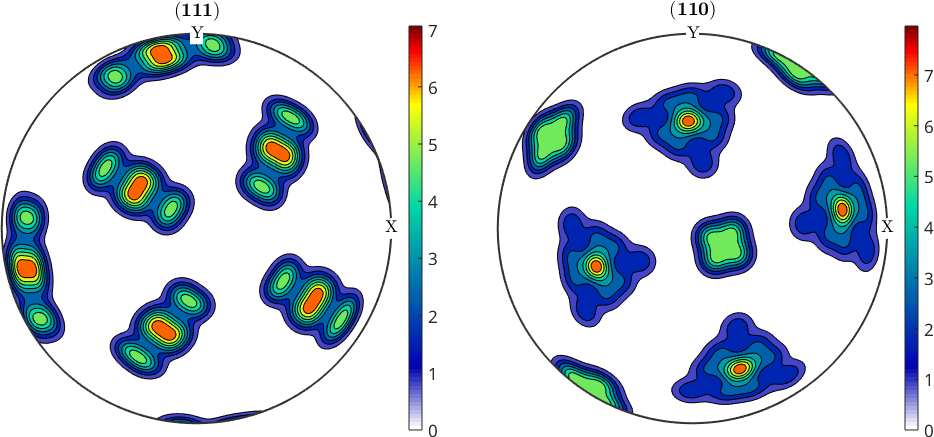
We observe that the transformed ODF computed by the latter approach is sharper and shows more details when compared with the ODF computed from discrete orientations. We may quantify this difference by computing the texture index of both ODFs
% texture index of the transformed ODF computed from discrete orientations
odfBSim = calcDensity(oriBSim)
norm(odfBSim)^2odfBSim = SO3FunHarmonic (Ferrite → y↑→x)
bandwidth: 25
weight: 1
ans =
3.4854% texture index of the directly computed transformed ODF
norm(odfB)^2ans =
17.4509