Harmonic Representation of Spherical Functions

Similarly as periodic functions may be represented as weighted sums of sines and cosines a spherical function \(f\) can be written as series of the form

\[ f({\bf v}) = \sum_{m=0}^M \sum_{l = -m}^m \hat f_m^l Y_m^l({\bf v}) \]

with respect to Fourier coefficients \(\hat f_m^l\) and the so called spherical harmonics \(Y_m^l({\bf v})\).

There exists various normalizations for the spherical harmonics. In MTEX the \(L_2\) norm of the spherical harmonics equals

\[\| Y_m^l \|_2 = 1\]

for all \(m,l\). For more information take a look on spherical harmonics and Integration of S2Fun's.

Within the class S2FunHarmonic spherical functions are represented by their Fourier coefficients which are stored in the field fun.fhat. As an example lets define a harmonic function which Fourier coefficients \(\hat f_0^0 = 1\), \(\hat f_1^{-1} = 0\), \(\hat f_1^0 = 3\) and \(\hat f_1^1 = 0\)

fun = S2FunHarmonic([1;0;3;0])

plotx2north
plot(fun)

fun = S2FunHarmonic
  bandwidth: 1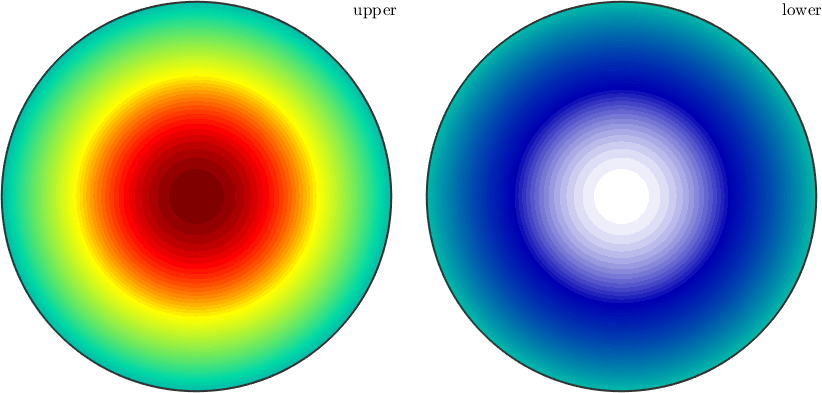
  isReal: true

This function has the cut off degree \(M=1\). As a rule of thumb: smooth functions require only a small cut off degree whereas functions with jumps or sharp edges requires a high cut off degree. If the cut off degree is chosen to small truncation error in the form of high order oscillations are observable like in the following demonstration for the cut off degrees \(M=64\) and \(M=32\).

sF = sqrt(abs(S2Fun.smiley('bandwidth',256)));

clf;
for bw = [256 128 64 32 16 8]
  sF.bandwidth = bw;
  nextAxis;
  pcolor(sF, 'upper','colorRange',[0,0.75]);
  mtexTitle(['M = ' num2str(bw)]);
end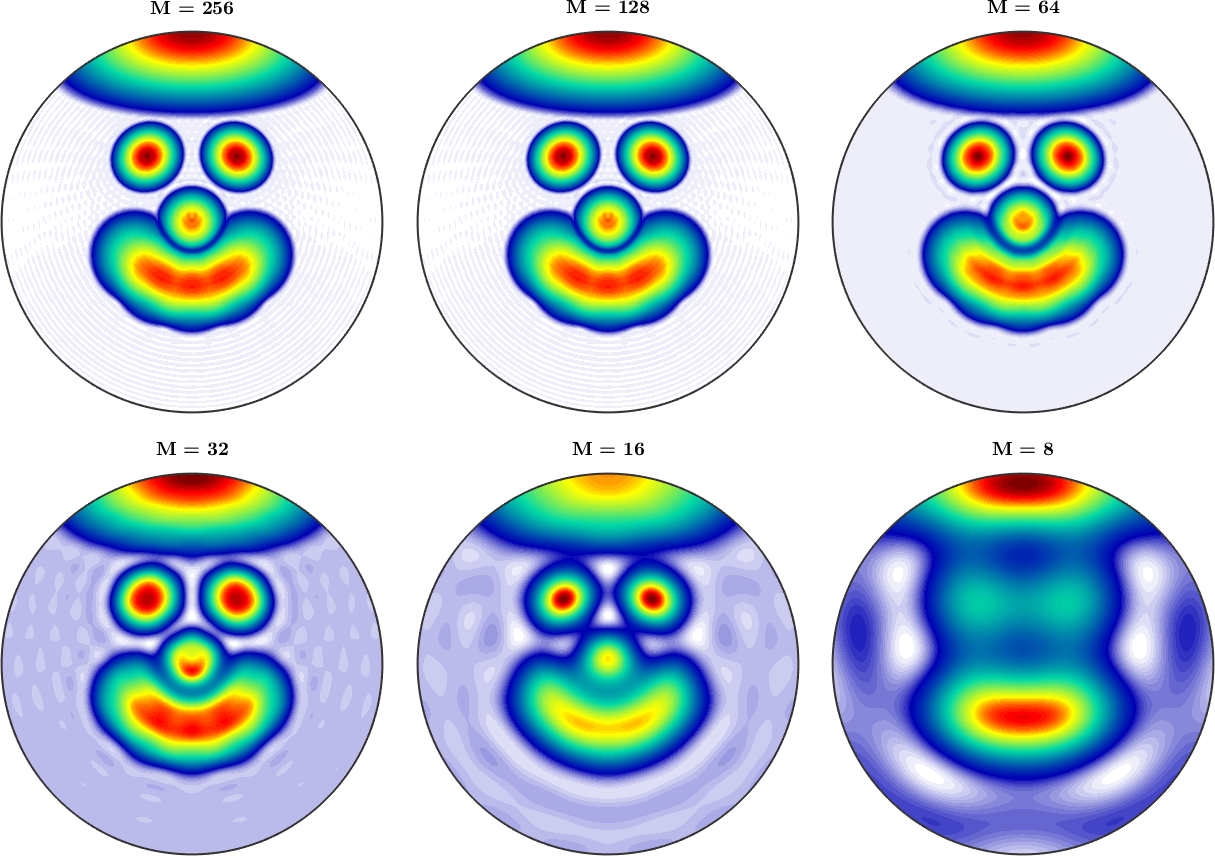

The computation of the Fourier coefficients can be done in several ways. Lets first assume that the function \(f\) is known explicitly, e.g., \(f({\bf v})=({\bf v} \cdot {\bf x})^3\). In MTEX we can express this as

fun = @(v) dot(v,vector3d.X).^9;

Now we can compute the Harmonic representation of this function and turn it into a variable of type S2FunHarmonic using the command S2FunHarmonic.quadrature

S2F = S2FunHarmonic.quadrature(fun)

plot(S2F,'upper')

S2F = S2FunHarmonic
  bandwidth: 128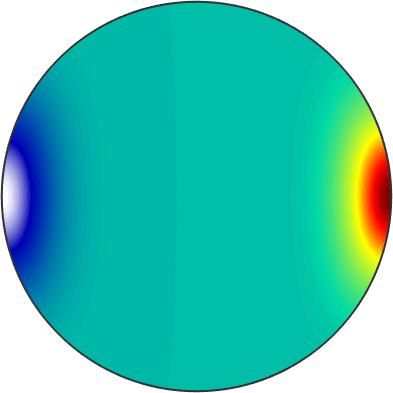
  isReal: true

We observe that by default Fourier coefficients up the harmonic cut off degree \(M=128\) are computed. This default value can changed using the option 'bandwidth'. The decay of the Fourier coefficients can be visualized using the command plotSpektra which plot for each harmonic degree \(m\) the sum of the squared moduli of the corresponding Fourier coefficients, i.e. \(\sum_{k=-m}^m \lvert \hat f_m^k\rvert^2\)

close all
plotSpektra(S2F)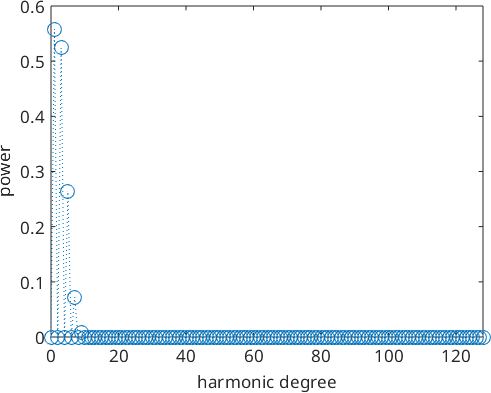

In the present example we observe that almost all Fourier coefficients are zero except for very first one. Hence, it might be reasonable to restrict the cut of degree to the non zero Fourier coefficients

% restrict to non zero Fourier coefficients
S2F = S2F.truncate

% power plot
plotSpektra(S2F,'linewidth',2)

S2F = S2FunHarmonic
  bandwidth: 9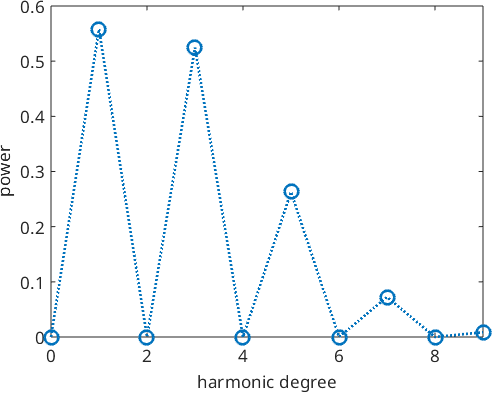
  isReal: true

In The robust estimation of these Fourier coefficients from discrete data is discussed in the section Spherical Approximation

In particular all operations on those functions are implemented as operations on the Fourier coefficients.

The crucial parameter when representing spherical functions by their harmonic series expansion is the harmonic cut off degree \(M\). .

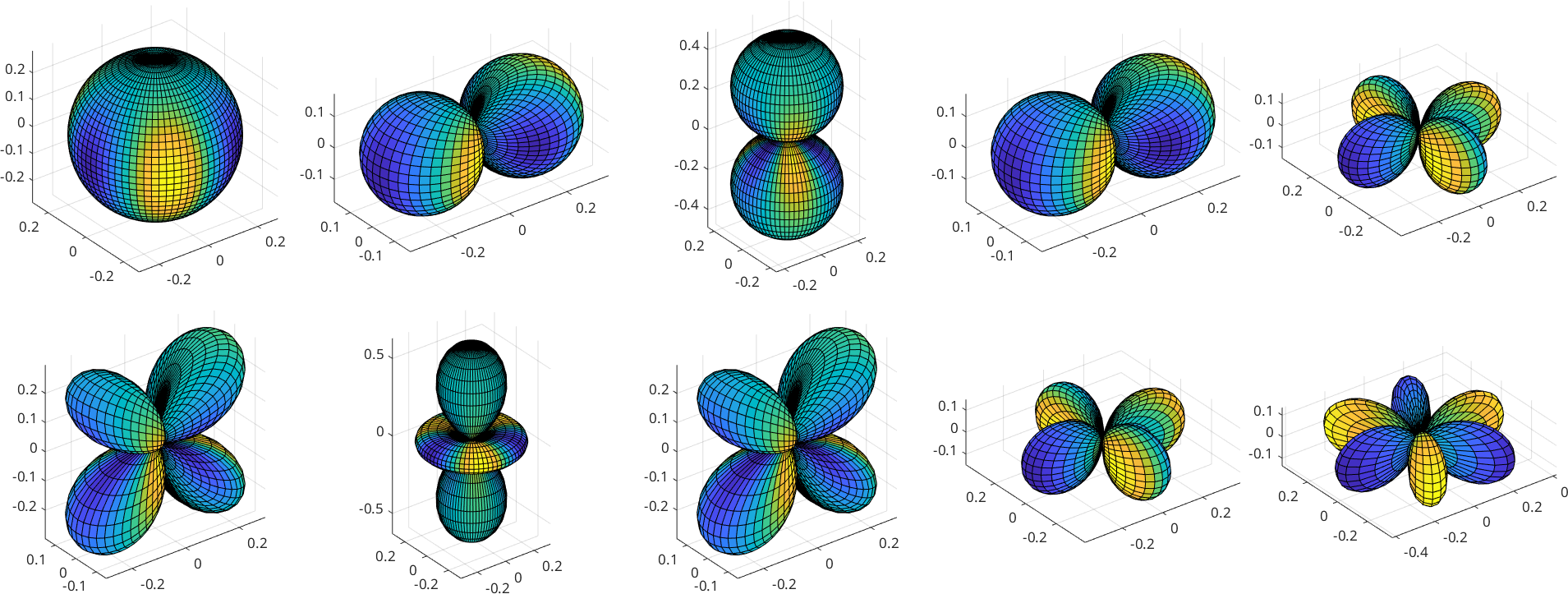
To conclude this session we plot the first ten spherical harmonics

surf(S2FunHarmonic(eye(10)))