Spherical Kernel Functions

A spherical kernel \(\psi\) is a spherical function that depends only on the angle towards the north pole \(e_3\),

psi = S2DeLaValleePoussinKernel('halfwidth',10*degree)

surf(psi,'resolution',2*degree,'EdgeColor','none')
hold on
arrow3d(2.4*zvector,'labeled','arrowwidth',0.01)
hold off
axis off

psi = S2DeLaValleePoussinKernel
  bandwidth: 25
  halfwidth: 10°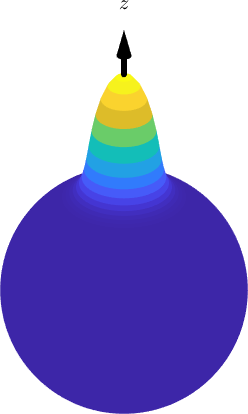

The dependency of the angle becomes more when plot along meridian

close all
plot(psi,'linewidth',2,'symmetric')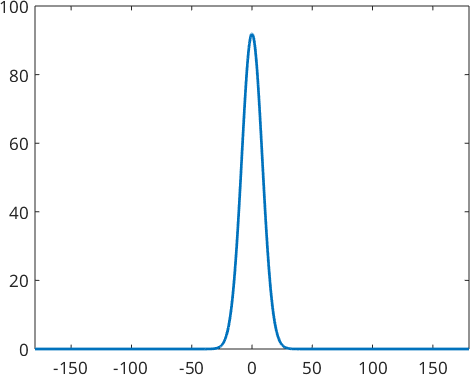

Examples of spherical kernel functions are

Fourier coefficients

Using mathematical notation we define this spherical kernel functions in the following way:

Every spherical kernel function \(\Psi\colon \mathcal{S}_2 \to \mathbb{R}\) can be associated with a function \(\psi \colon [-1,1] \to \mathbb R\) defined on the interval \([-1,1]\) by \(\Psi(\vec v) = \psi(t)\) with \(t=\cos(\sphericalangle(\vec v,\vec e_3)) = \vec v \cdot \vec e_3\). It turns out to be useful to approximate \(\psi\) by a expansion into Legendre polynomials \(P_n\colon[-1,1]\to\IR\) of degree \(n\), i.e.,

\[ \psi(t) = \sum\limits_{n=0}^{\infty} (2n+1)\,\hat\psi_n \, \mathcal P_{n}(t). \]

Here, \(\hat\psi_n\) is called the Fourier coefficient or spherical harmonic coefficient of degree \(n\). These are the same coefficients that are used for representing S2FunHarmonic's. Note, that in general, a S2FunHarmonic has \((2n+1)\) Fourier coefficients for every degree \(n\). Here we have only one coefficient, due to the radial symmetry of the S2Kernel. The others are zero.

The Fourier coefficients of an S2Kernel can be easily visualized using the command plotSpectra.

plotSpektra(psi,'linewidth',2)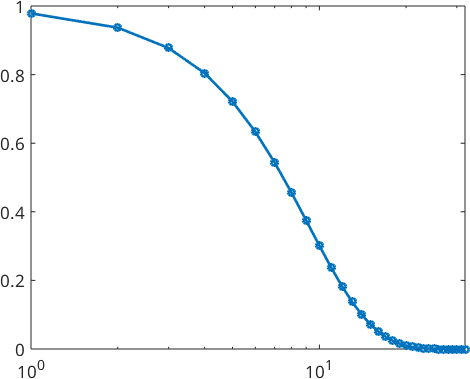

However, within the class S2Kernel, kernel functions are represented by their Legendre coefficients \((2n+1)\,\hat\psi_n\), which are stored in the field psi.A.

Applications

Spherical kernel functions have different applications in MTEX. Those include

The de la Vallee Poussin Kernel

The spherical de la Vallee Poussin kernel is defined by

\[ K(t) = (1+\kappa)\,(\frac{1+t}{2})^{\kappa}\]

for \(t\in[0,1]\). The de la Vallee Poussin kernel additionally has the unique property that for a given halfwidth it can be described exactly by a finite number of Fourier coefficients. This kernel is recommended for Texture analysis as it is always positive and there is no truncation error in Fourier space.

Hence we can define the de la Vallee Poussin kernel \(\psi_{\kappa}\) depending on a parameter \(\kappa \in \mathbb N \setminus \{0\}\) by its finite Legendre polynomial expansion

\[ \psi_{\kappa}(t) = \sum\limits_{n=0}^{L} (2n+1)\,\hat\psi_n(\kappa)\,\mathcal P_{n}(t).\]

We obtain the Fourier coefficients \(\hat\psi_n(\kappa)\) by \(\hat\psi_0=1\), \(\hat\psi_1=\frac{\kappa}{6+3\kappa}\) and the three term recurrence relation

\[ (\kappa+l+2)(2l+3)\, \hat\psi_{l+1} = -(2l+1)^2\,\hat\psi_l + (\kappa-l+1)(2l-1)\,\hat\psi_{l-1}.\]

Lets construct two of this kernels.

psi1 = S2DeLaValleePoussinKernel('halfwidth',15*degree)
psi2 = S2DeLaValleePoussinKernel('halfwidth',20*degree)

plot(psi1,'linewidth',2,'symmetric')
hold on
plot(psi2,'linewidth',2,'symmetric')
hold off
legend('halfwidth = 15°','halfwidth = 20°')

psi1 = S2DeLaValleePoussinKernel
  bandwidth: 17
  halfwidth: 15°
 
 
psi2 = S2DeLaValleePoussinKernel
  bandwidth: 13
  halfwidth: 20°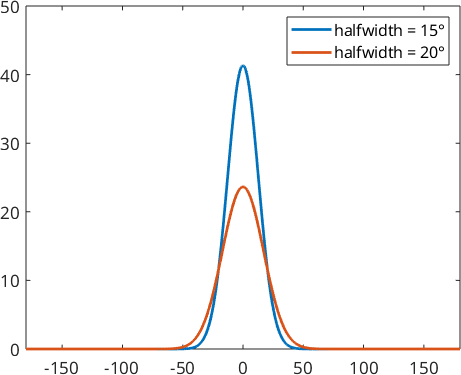

Here the parameter \(\kappa\) is \(40.34\) for function \(\psi_1\) and \(22.64\) in function \(\psi_2\).

We also take a look at the Fourier coefficients

plotSpektra(psi1,'linewidth',2)
hold on
plotSpektra(psi2,'linewidth',2)
hold off
legend('halfwidth = 15°','halfwidth = 20°')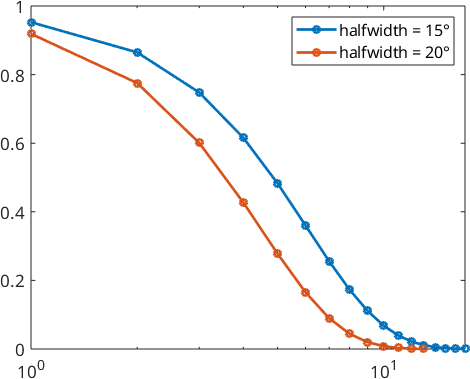

The Dirichlet Kernel

The spherical Dirichlet or Christoffel-Darboux kernel is recommended for calculating physical properties as the Fourier coefficients always have a value of one up to the specified bandwidth:

\[ \psi_N(t) = \sum\limits_{n=0}^N (2n+1) \, \mathcal P_{n}(t).\]

Lets construct two of them.

psi1 = S2DirichletKernel(10)
psi2 = S2DirichletKernel(5)

plot(psi1,'linewidth',2,'symmetric')
hold on
plot(psi2,'linewidth',2,'symmetric')
hold off
legend('bandwidth = 10','bandwidth = 5')

psi1 = S2DirichletKernel
  bandwidth: 10
  halfwidth: 180°
 
 
psi2 = S2DirichletKernel
  bandwidth: 5
  halfwidth: 180°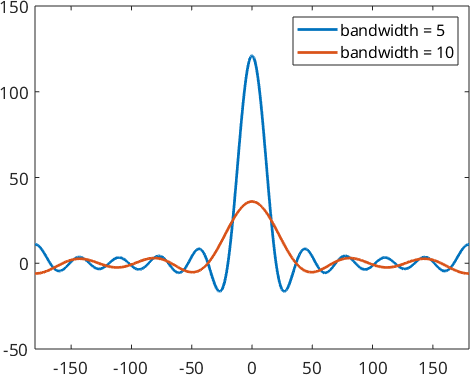

By looking at the Fourier coefficients we see, that they are exactly 1.

plotSpektra(psi1,'linewidth',2)
hold on
plotSpektra(psi2,'linewidth',2)
hold off
legend('bandwidth = 10','bandwidth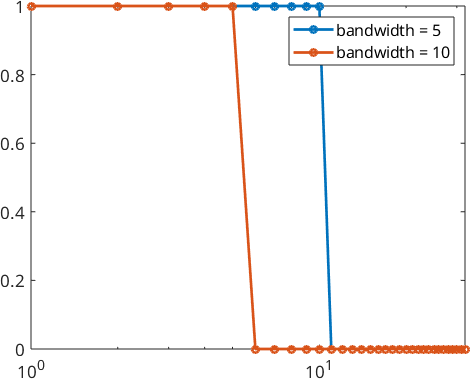 = 5')

The Bump kernel

The spherical bump kernel is a radial symmetric kernel function depending on the halfwidth \(r\in (0,pi)\). The function value is 0, if the angle is greater then the halfwidth \(r\). Otherwise it is 1.

The main problem of the bump kernel is that we need lots of Fourier coefficients to describe it. That possibly can result in high runtimes.

psi1 = S2BumpKernel(30*degree)
psi2 = S2BumpKernel(50*degree)

plot(psi1,'linewidth',2,'symmetric')
hold on
plot(psi2,'linewidth',2,'symmetric')
hold off
legend('halfwidth = 30°','halfwidth = 50°')

psi1 = S2BumpKernel
  bandwidth: 1000
  halfwidth: 30°
 
 
psi2 = S2BumpKernel
  bandwidth: 1000
  halfwidth: 50°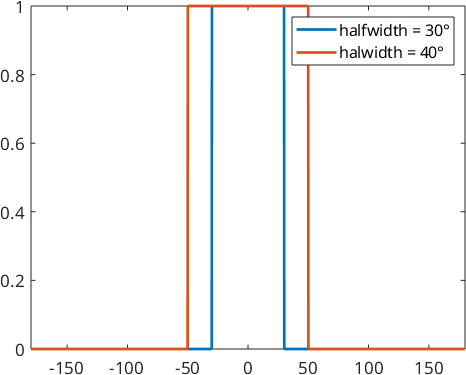

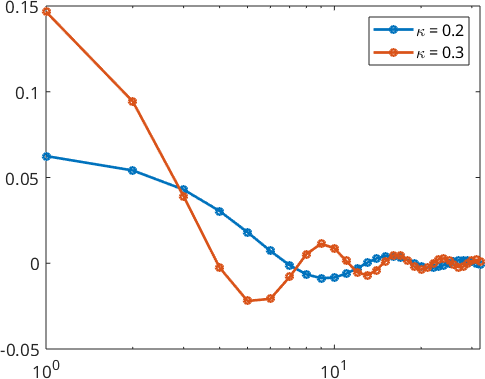
We also take a look at the Fourier coefficients

plotSpektra(psi1,'linewidth',2)
hold on
plotSpektra(psi2,'linewidth',2)
hold off
legend('halfwidth = 30°','halfwidth = 50°')