Unimodal ODF Shapes
In order to control the shape of unimodal ODF The class kernel is needed in MTEX to define the specific form of unimodal and fibre symmetric ODFs. It has to be passed as an argument when calling the methods uniformODF and fibreODF.
A kernel is defined by specifying its name and its free parameter. Alternatively one can also specify the halfwidth of the kernel. Below you find a list of all kernel functions supported by MTEX.
psi{1} = AbelPoissonKernel(0.79);
psi{2} = deLaValleePoussinKernel(13);
psi{3} = bumpKernel(35*degree);
psi{4} = DirichletKernel(3);
psi{5} = vonMisesFisherKernel(7.5);
psi{6} = GaussWeierstrassKernel(0.07);
psi{7} = fibreVonMisesFisherKernel(7.2);
psi{8} = SquareSingularityKernel(0.72);Lets visualize these kernel functions as one dimensional sections through the orientation space
% the kernel on SO(3)
close;
figure('position',[100,100,1000,450])
hold all
for i = 1:numel(psi)
plot(psi{i},'DisplayName',class(psi{i}));
end
hold off
legend(gca,'show','Location','eastoutside')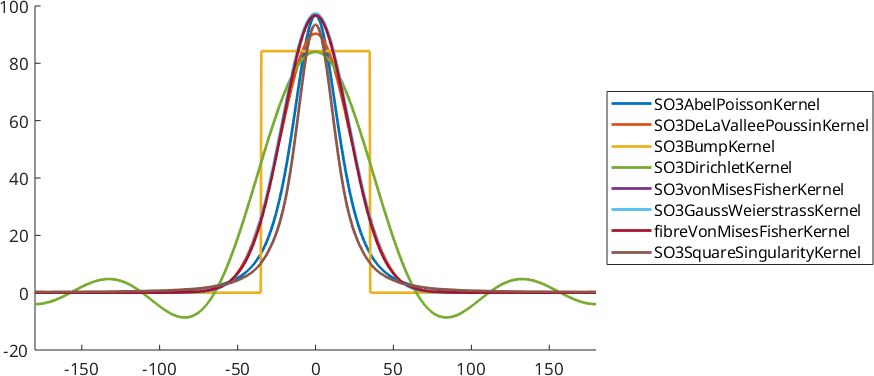
one dimensional sections through the corresponding PDF
close; figure('position',[100,100,1000,450])
hold all
for i = 1:numel(psi)
plotPDF(psi{i},'RK','DisplayName',class(psi{i}));
end
hold off
ylim([-5,20])
legend(gca,'show','Location','eastoutside')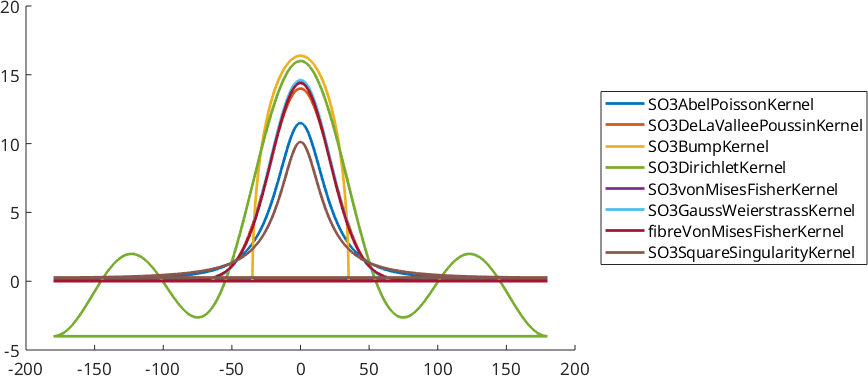
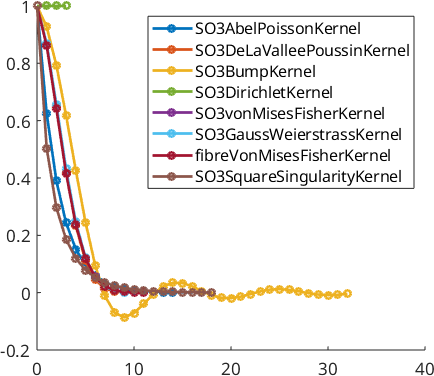
the Fourier coefficients of the kernels
close; figure('position',[100,100,500,450])
hold all
for i = 1:numel(psi)
plotFourier(psi{i},'bandwidth',32,'linewidth',2,'DisplayName',class(psi{i}));
end
hold off
legend(gca,'show')