Inverse Pole Figure edit page

Inverse pole figures are two dimensional representations of orientations. To illustrate this we define a random orientation with trigonal crystal symmetry

cs = crystalSymmetry('321');
ori = orientation.rand(cs)
ori = orientation (321 → y↑→x)
 
  Bunge Euler angles in degree
     phi1     Phi    phi2
  156.958 161.468 197.878

Starting point is a fixed specimen direction r, e.g.,

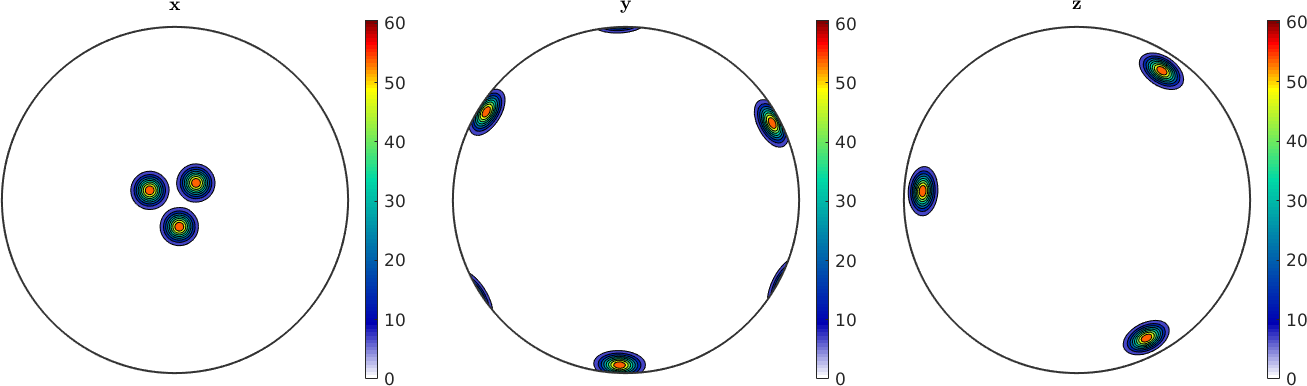
r = vector3d.Z;

Next the crystal direction that aligns with specimen direction r according to the orientation ori is computed and plotted in a spherical projection

h = inv(ori) * r

plot(h.symmetrise,'fundamentalRegion')
h = Miller (321)
       h       k       i       l
  0.0667 -0.3025  0.2357 -0.9481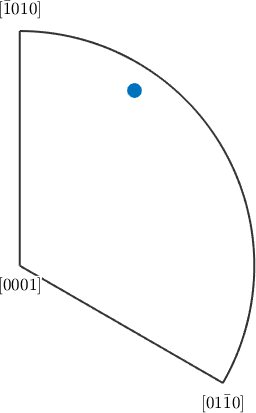

A shortcut for the above computations is the command plotIPDF which takes as second argument an arbitrary list of specimen directions r 

% a pole figure plot
plotIPDF(ori,[vector3d.X,vector3d.Y,vector3d.Z])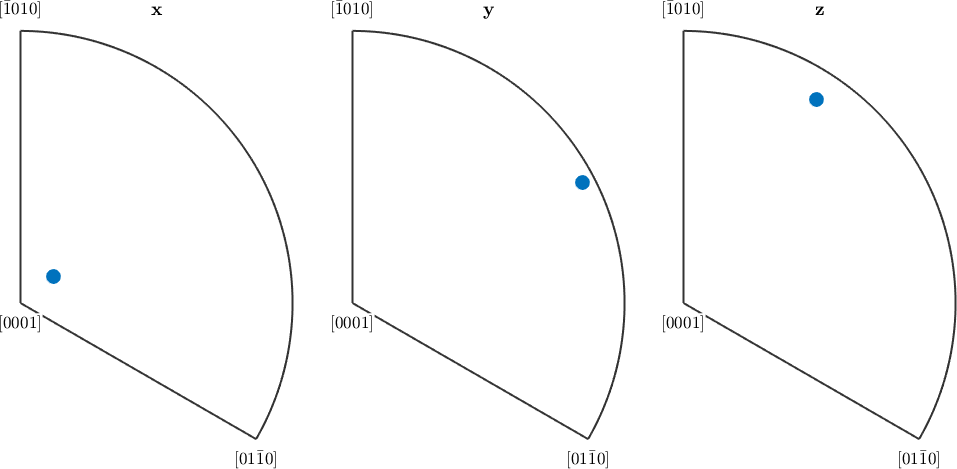

Contour plots

Using the option 'contourf' we may turn those scatter plots into contour plots.

plotIPDF(ori,[vector3d.X,vector3d.Y,vector3d.Z],'contourf')
mtexColorbar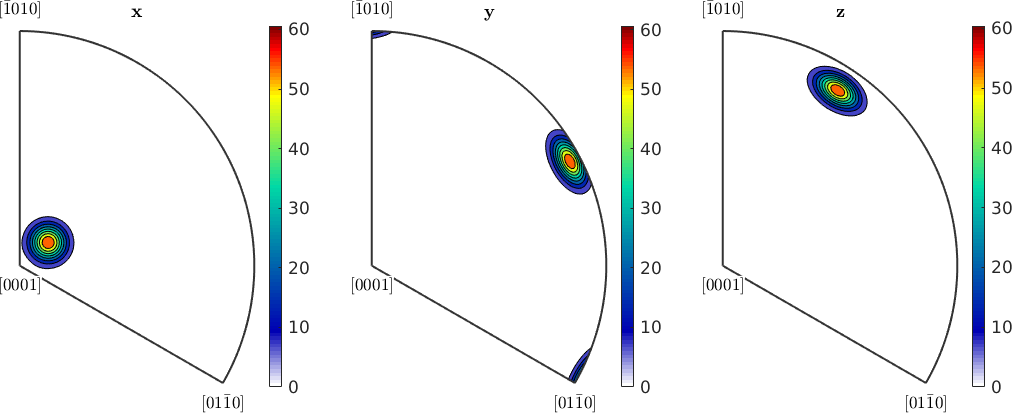

Note that by default only the fundamental sector with respect to the crystal symmetry is plotted. In order to plot the entire sphere use the option 'complete'.

plotIPDF(ori,[vector3d.X,vector3d.Y,vector3d.Z],'contourf','complete','upper')
mtexColorbar