By quasi crystals we mean materials with a non crystallographic symmetry group, e.g. including a pentagonal or decagonal symmetry axis. Such symmetry groups do not lead to perfect translational invariant lattices and hence are not crystals.
Setting up a non standard symmetry group can be done by specifying all its symmetry elements. To illustrate this definition lets consider the symmetry group corresponding to the dodecaeder which is generated by a 5 fold and a 3 fold symmetry axis.
rot2 = rotation.byAxisAngle(vector3d.Z,180*degree);
a5 = normalize(vector3d(0,2/(1+sqrt(5)),1));
rot5 = rotation.byAxisAngle(a5,72*degree);
%rot3 = rotation.byAxisAngle(vector3d.byPolar(20.9054*degree,90*degree),120*degree);
cs = crystalSymmetry.byElements([rot5,rot2])
plot(cs,'symbolSize',0.5,'projection','eangle','grid','on')cs = crystalSymmetry
symmetry : unkwown
elements : 60
a, b, c : 1, 1, 1
alpha, beta, gamma: 90°, 90°, 90°
reference frame : X||a, Y||b, Z||c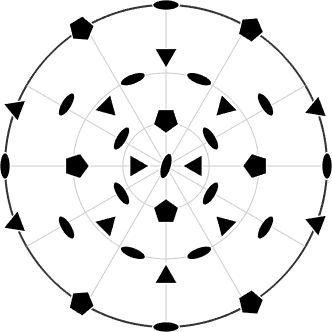
Many of the MTEX methods do work also with quasi symmetries. E.g. we can identify the fundamental sector by
hold on
plot(cs.fundamentalSector,'color','red')
hold off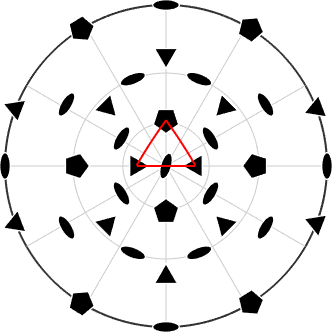
the fundamental region is orientation space, which is exactly a dodecaeder,
oR = cs.fundamentalRegion;
plot(oR)
axis off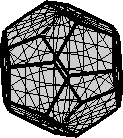
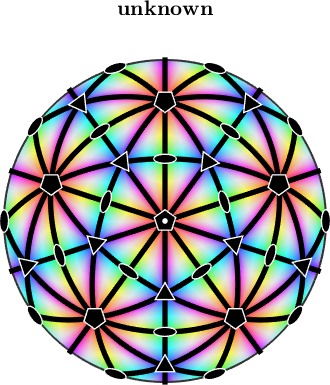
or define an appropriate color key
ipfKey = ipfHSVKey(cs);
plot(ipfKey,'complete','upper','resolution',0.5*degree)
hold on
plot(cs,'SymbolSize',0.6,'linewidth',1)
hold off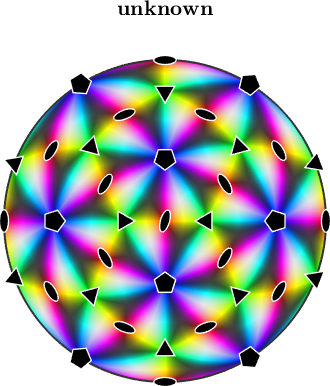
We may also choose a different setup where the 5 fold axis is aligned parallel to z
rot5 = rotation.byAxisAngle(zvector,72*degree);
rot3 = rotation.byAxisAngle(vector3d('polar',37.377*degree,0) ,120*degree);
cs = crystalSymmetry.byElements([rot5,rot3])
plot(cs,'symbolSize',0.5,'projection','eangle','grid','on')cs = crystalSymmetry
symmetry : unkwown
elements : 60
a, b, c : 1, 1, 1
alpha, beta, gamma: 90°, 90°, 90°
reference frame : X||a, Y||b, Z||c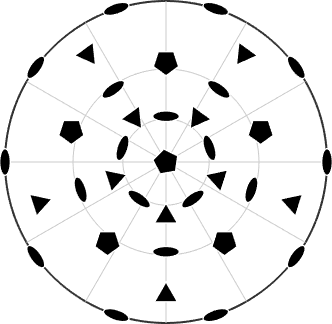
or include the inversion
cs = crystalSymmetry.byElements([rot5,rot3,rotation.inversion])
ipfKey = ipfHSVKey(cs);
plot(ipfKey,'complete','upper','resolution',0.5*degree)
hold on
plot(cs,'symbolSize',0.6,'linewidth',2)
hold offcs = crystalSymmetry
symmetry : unkwown
elements : 120
a, b, c : 1, 1, 1
alpha, beta, gamma: 90°, 90°, 90°
reference frame : X||a, Y||b, Z||c