Grids of Orientation edit page

In many use cases one is interested in grid of orientations that somehow uniformly cover the orientation space. The simplest way of generating equispaced orientations with given resolution is by the command

% define a crystal symmetry
cs = crystalSymmetry('432')

% define a grid of orientations
ori = equispacedSO3Grid(cs,'resolution',5*degree)
cs = crystalSymmetry
 
  symmetry: 432    
  elements: 24     
  a, b, c : 1, 1, 1
 
 
ori = SO3Grid (432 → y↑→x)
  grid: 4958 orientations, resolution: 5°

Lets visualize them

plot(ori,'axisAngle')
plot 2000 random orientations out of 4958 given orientations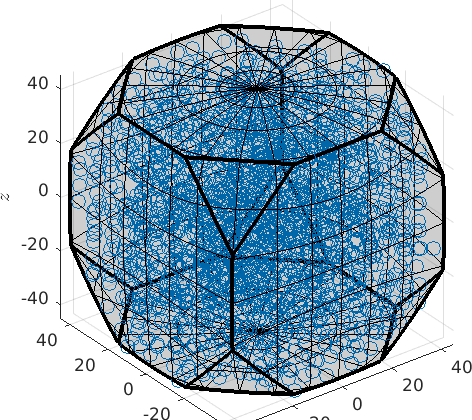

Check for equidistribution

odf = unimodalODF(ori)

plotPDF(odf,Miller({1,0,0},{1,1,0},{1,1,1},cs))
mtexColorbar
odf = SO3FunRBF (432 → y↑→x)
 
  multimodal components
  kernel: de la Vallee Poussin, halfwidth 10°
  center: 4958 orientations, resolution: 5°
  weight: 1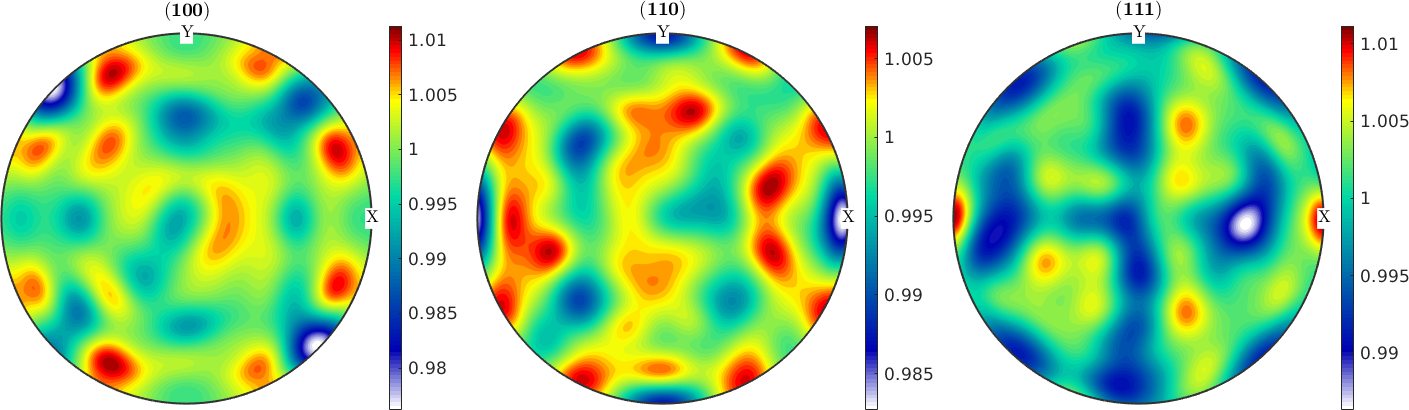
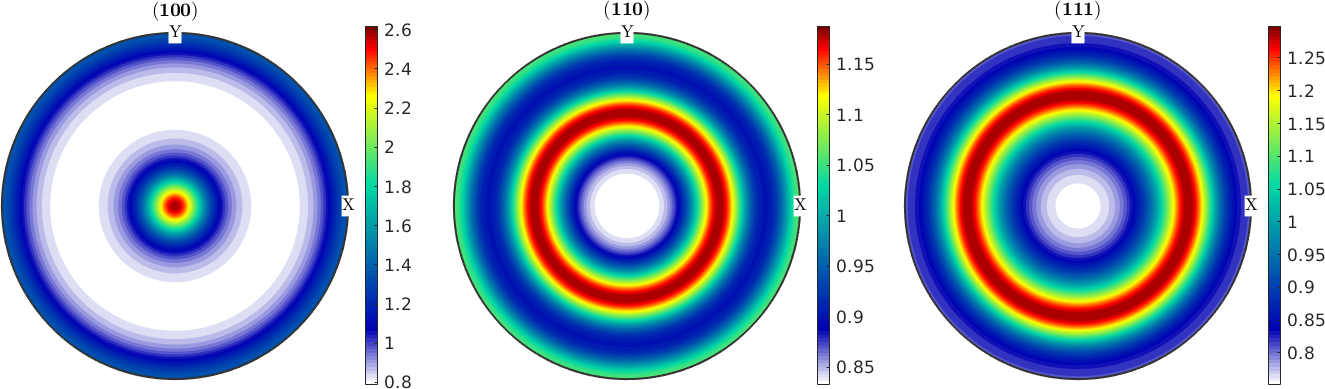
ori = regularSO3Grid(cs,'resolution',5*degree)
ori = orientation (432 → y↑→x)
  size: 72 x 19 x 18
plot(ori,'axisAngle')
plot 2000 random orientations out of 24624 given orientations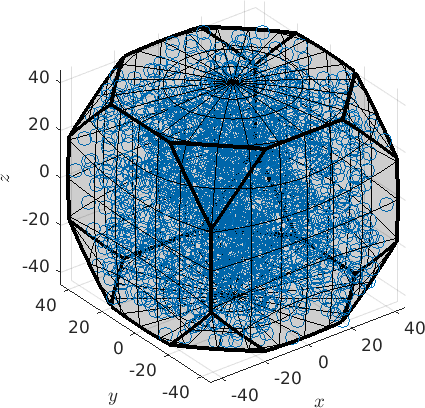
odf = unimodalODF(ori)

plotPDF(odf,Miller({1,0,0},{1,1,0},{1,1,1},cs))
mtexColorbar
odf = SO3FunRBF (432 → y↑→x)
 
  multimodal components
  kernel: de la Vallee Poussin, halfwidth 10°
  center: 24624 orientations