On this page we consider the problem of determining the harmonic expansion (SO3FunHarmonic) of a smooth orientation dependent function \(f(\mathtt{ori})\) given a list of orientations \(\mathtt{ori}_m\) and a list of corresponding values \(v_m\). These values may be the volume of crystals with a specific orientation, as in the case of an ODF, or any other orientation dependent physical property.
A more general documentation about approximation of discrete data in MTEX can be found in the section Approximating Orientation Dependent Functions from Discrete Data.
In general we should favor harmonic approximation, if the underlying function comes from some physical experiment and is no density function or if we have a very big number of nodes and function values given.
Exact interpolation is computational hard if we have a high number of nodes and function values given. We have more freedom, if we do not restrict ourselves to much to the given function values. The same happen, if the data are noisy or not exact, as it is often the case in physical experiments, where exact interpolation makes no sense, since it would result into overfitting.
In exchange we want the approximated function to be reasonably smooth. Therefore we can choose sparser interpolation matrices which reduce the computational costs.
In the following we take a look on the approximation problem from general approximation theory, where we compared the harmonic approximation with kernel approximation.
Here we additionally assume that our function values are noisy.
fname = fullfile(mtexDataPath, 'orientation', 'dubna.csv');
[ori, S] = orientation.load(fname,'columnNames',{'phi1','Phi','phi2','values'});
val = S.values + randn(size(S.values)) * 0.05 * std(S.values);
plotSection(ori,val,'all','sigma')
Harmonic Approximation (without Regularization)
The basic strategy is to approximate the data by a SO3FunHarmonic (Harmonic series), i.e. a series of Wigner-D functions, see SO3FunHarmonicSeries Basics of rotational harmonics.
For that, we seek the so-called Fourier coefficients \({\bf \hat f} = (\hat f^{0,0}_0,\dots,\hat f^{N,N}_N)^T\) such that
\[ f(x) = \sum_{n=0}^N\sum_{k,l = -n}^n \hat f_n^{k,l} D_n^{k,l}(x) \]
approximates our data reasonable well. A basic strategy to achieve this is through least squares approximation, where we compute the Fourier coefficients of \(f\) by minimizing the functional
\[ \sum_{m=1}^M|f(x_m)-v_m|^2 \]
for the given data points \((x_m,v_m)\), \(m=1,\dots,M\). Here \(x_m\) denotes the given orientations and \(v_m\) the corresponding function values.
This least squares problem can be solved by the lsqr method from MATLAB, which efficiently seeks for roots of the derivative of the given functional (also known as normal equation). In the process we compute the matrix-vector product with the Fourier-matrix multiple times, where the Fourier-matrix is given by
\[ F = [D_n^{k,l}(x_m)]_{m = 1,\dots,M;~n = 0,\dots,N,\,k,l = -n,\dots,n}. \]
This matrix-vector product can be computed efficiently with the use of the nonequispaced SO(3) Fourier transform NSOFT or faster by the combination of a so-called Wigner-transform together with a NFFT.
However, we end up with the Fourier coefficients of our approximation \(f\).
In MTEX approximation by harmonic expansion is computed by the command interp with the flag 'harmonic'. Here MTEX internally call the underlying SO3FunHarmonic.interpolate command of the class SO3FunHarmonic.
The approximation process described above does not use regularization. Therefore, for demonstration purposes, we'll set the parameter 'regularization' to \(0\) for the moment. More on this topic later.
We can specify the desired bandwidth of the resulting SO3FunHarmonic by the parameter bandwidth.
SO3F1 = interp(ori, val,'harmonic','regularization',0,'bandwidth',17)
% SO3F1 = SO3FunHarmonic.interpolate(ori, val,'regularization',0,'bandwidth',17)
plot(SO3F1,'sigma')SO3F1 = SO3FunHarmonic (1 → y↑→x)
bandwidth: 17
weight: 0.99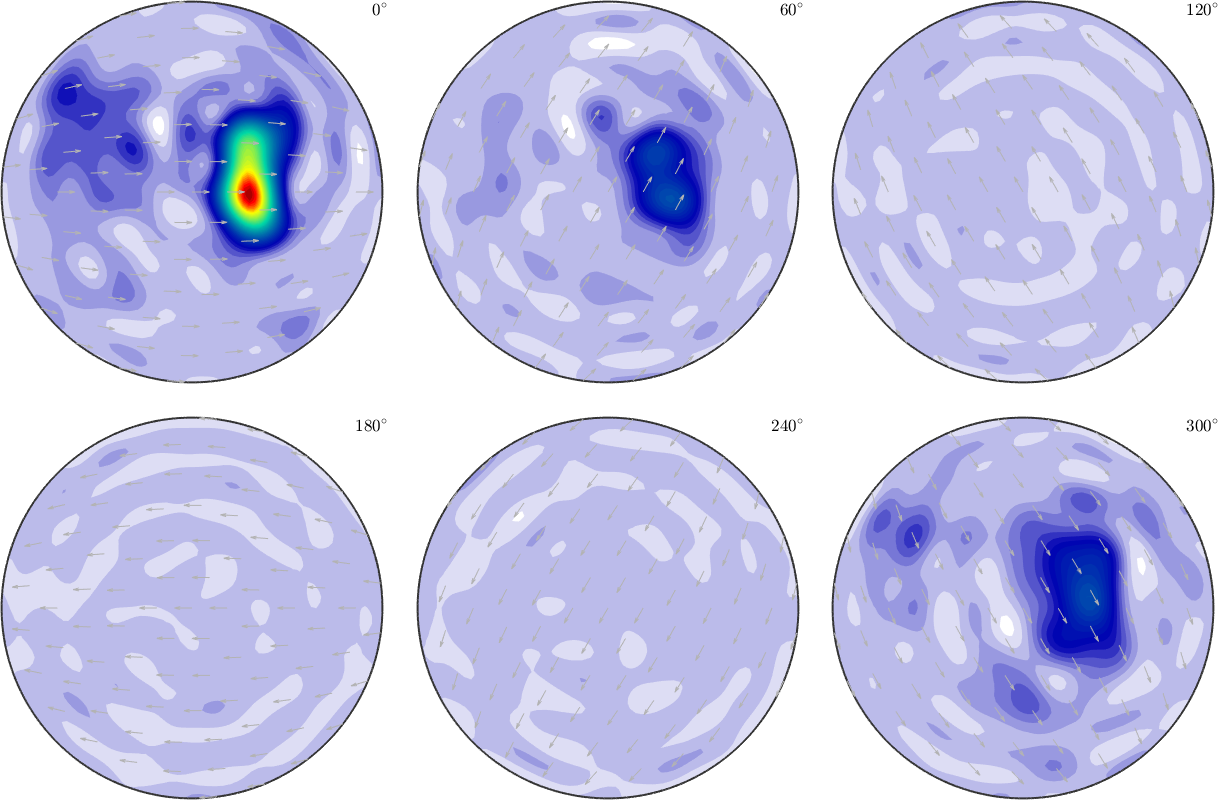
The choice of a low bandwidth yields a smooth approximation. One has to keep in mind that we can not expect the error in the data nodes to be zero, as this would mean overfitting to the noisy input data.
norm(eval(SO3F1, ori) - val) / norm(val)ans =
0.0779If we choose the bandwidth to high and try to compute more Fourier coefficients as there are data points given, then we are in the overdetermined case and obtain oversampling.
SO3F2 = interp(ori, val,'harmonic','regularization',0,'bandwidth',32)
plot(SO3F2,'sigma')Warning: The oversampling factor in the approximation process is
0.43553. This could lead to a bad approximation. You may should
not set the regularization parameter to 0 in the approximation
method.
SO3F2 = SO3FunHarmonic (1 → y↑→x)
bandwidth: 32
weight: 0.25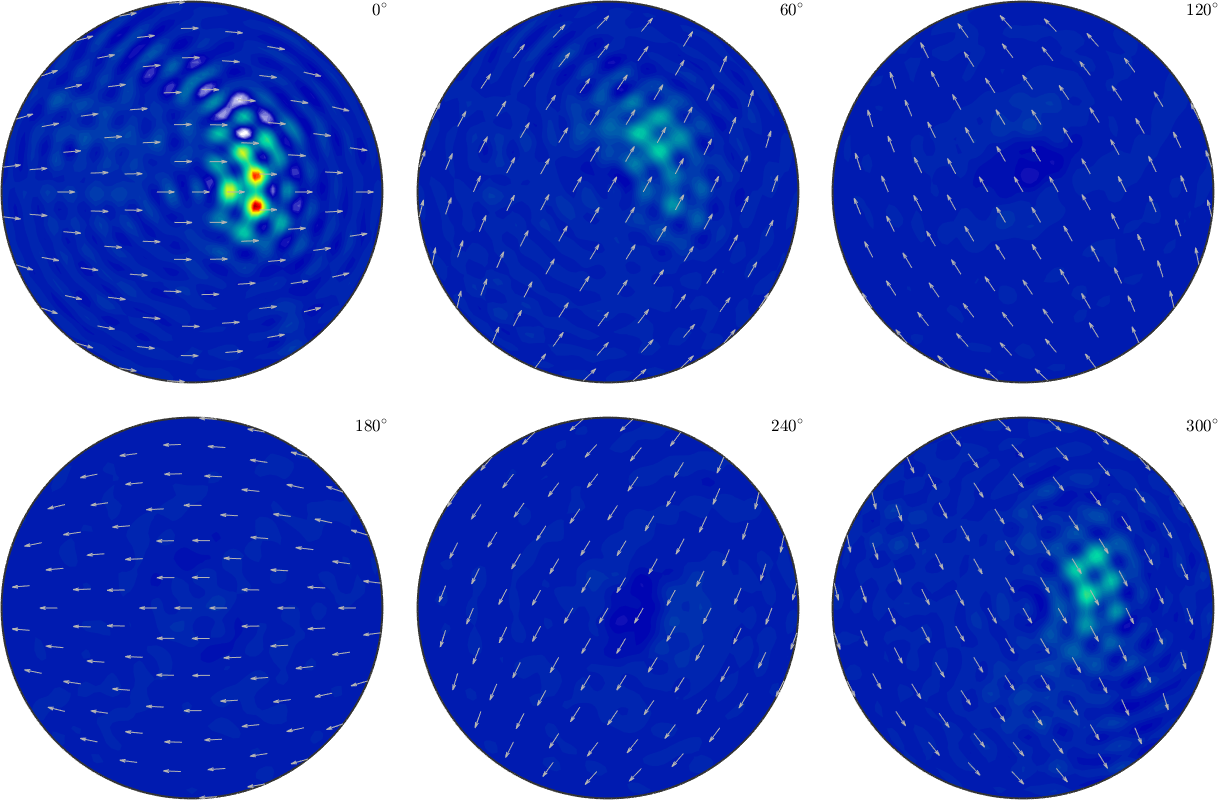
Here the error is much smaller, since we did overfitting to the noisy input data.
norm(eval(SO3F2, ori) - val) / norm(val)ans =
0.0123Lets take a look on the Fourier coefficients of this approximations.
plotSpektra([SO3F1,SO3F2])
legend('Bandwidth 17','Bandwidth 32')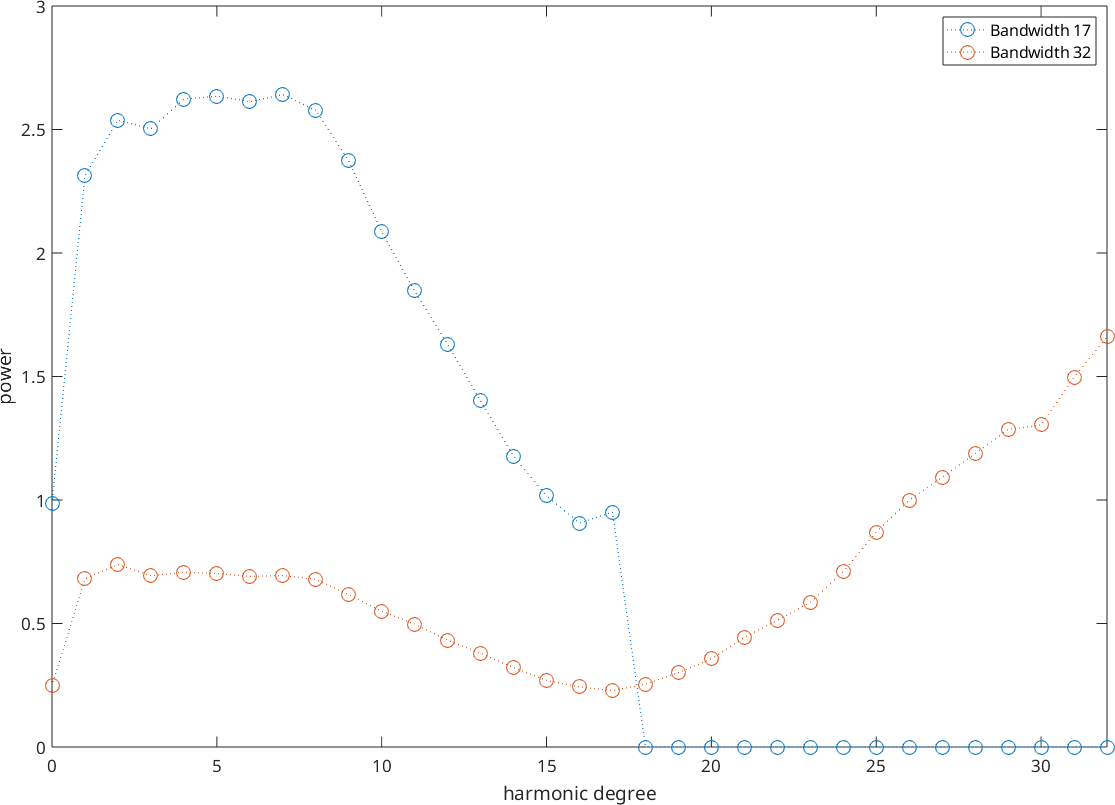
We can see that they do not converge to zero, as it would be the case if the approximation is continuous. The increasing behavior of the Fourier coefficients is a consequence of overfitting, which can also be seen from the oscillations in the above plots.
We will overcome this effects in the following by regularization.
Harmonic Approximation with Regularization
Lets assume we have a low number of data points given, but the desired function is relatively sharp. Then we will try to compute a SO3FunHarmonic with high bandwidth and we are in the underdetermined case, since we try to compute many Fourier coefficients from a lower number of data points, which results into overfitting. We can overcome this by additionally demanding that the approximation \(f\) should be smooth.
Therefore we do so-called Tikhonov regularization, which means that we penalize oscillations by adding the norm of \(f\) to the energy functional, which is minimized by the lsqr solver. Hence we now minimize the functional
\[ \sum_{m=1}^M|f(x_m)-v_m|^2 + \lambda \|f\|^2_{H^s}\]
where \(\lambda\) is the regularization parameter. The Sobolev norm \(\|.\|_{H^s}\) of an SO3FunHarmonic \(f\) with Fourier coefficients \(\hat{f}\) reads as
\[\|f\|^2_{H^s} = \sum_{n=0}^N (2n+1)^{2s} \, \sum_{k,l=-n}^n|\hat{f}_n^{k,l}|^2.\]
The Sobolev index \(s\) describes how smooth our approximation \(f\) should be, because the larger \(s\) is, the faster the Fourier coefficients \(\hat{f}_n^{k,l}\) converge towards 0 and the smoother is the approximation \(f\).
The command SO3FunHarmonic.interpolate of the class SO3FunHarmonic applies regularization by default. The default regularization parameter is \(\lambda = 5\cdot 10^{-7}\) and the default Sobolev index \(s=2\);
SO3F3 = interp(ori, val,'harmonic','bandwidth',32)
% SO3F3 = SO3FunHarmonic.interpolate(ori,val,'bandwidth',32)
plot(SO3F3,'sigma')SO3F3 = SO3FunHarmonic (1 → y↑→x)
bandwidth: 32
weight: 0.99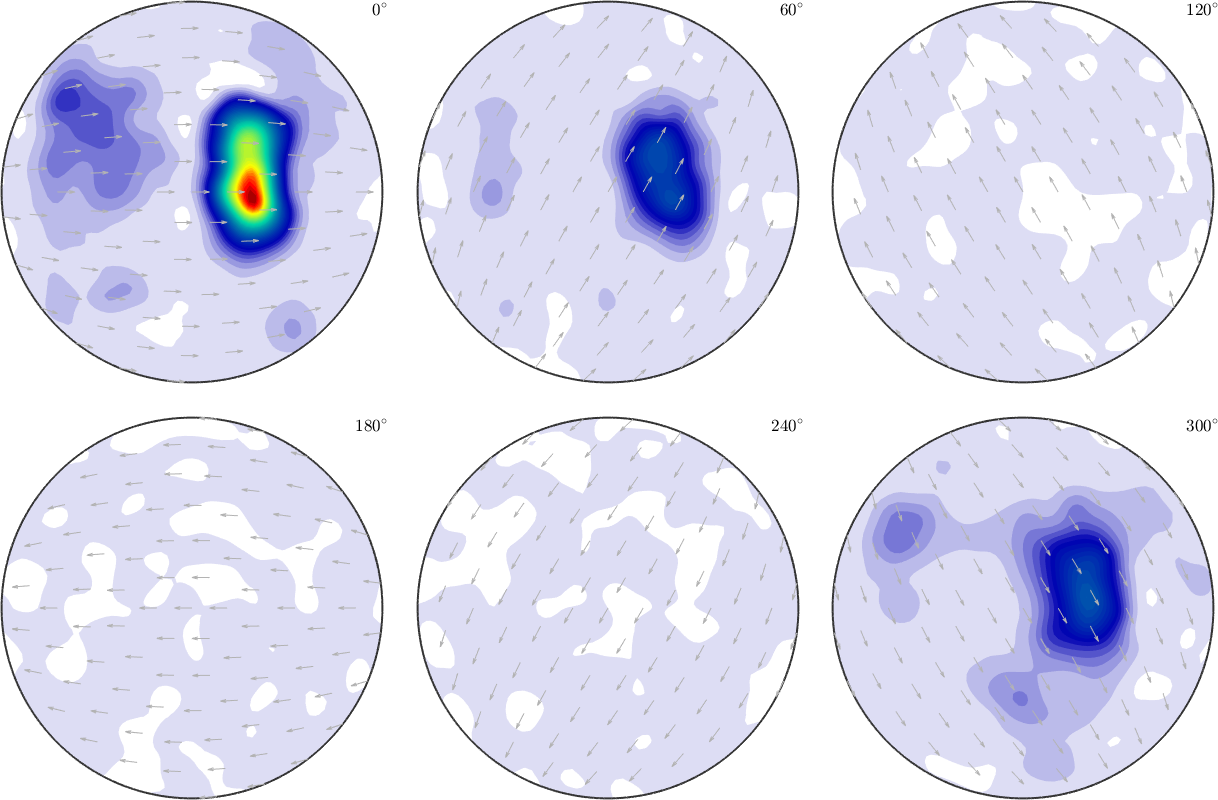
We can immediately see, that we have a much smoother function.
This smoothing results in a larger error in the data points, which may not be much important since we had noisy function values given, where we don't know the exact values anyways.
norm(eval(SO3F3, ori) - val) / norm(val)ans =
0.0824Note that this Error is not the value of the above energy functional which is minimized by lsqr.
It is not easy to specify the parameter \(\lambda\), which describes the intensity of regularization. If we choose a value that is too large, we smooth the function too much. If \(\lambda\) is chosen too small, there is almost no regularization and we get oscillations.
Lets try to regularize with different regularization parameters \(\lambda\) and plot the sigma sections of \(0^{\circ}\):
% approximation
reg = [1,1e-1,1e-2,1e-3,1e-4,1e-5,1e-6,1e-7,1e-8,1e-9,1e-10,1e-11,1e-12,1e-13,1e-14];
for i=1:15
SO3F4(i) = interp(ori,val,'harmonic','bandwidth',32,'regularization',reg(i));
end
% plotting
plot(SO3F4(1),'sigma',0*degree)
legend(['\lambda = ',num2str(reg(1))])
for i=2:15
nextAxis
plot(SO3F4(i),'sigma',0*degree)
legend(['\lambda = ',num2str(reg(i))])
end
setColorRange('tight')
mtexColorbar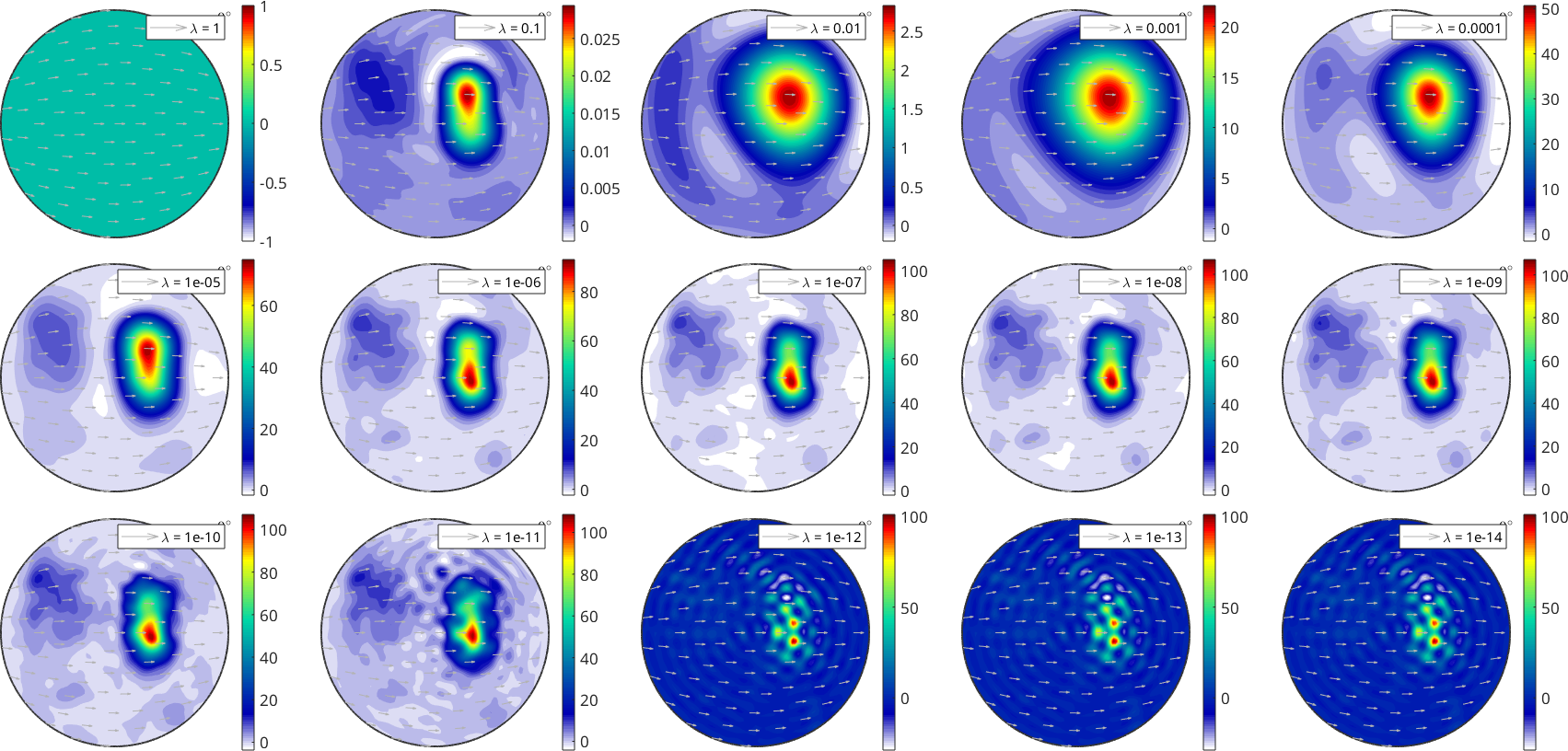
For large regularization parameters the function is almost 0. The regularization term has to much impact on the energy functional, compared to the error term. As the regularization parameter is gradually reduced, the influence of the error term increases. Higher frequencies and stronger changes in the function values are no longer penalized as much. However, as soon as the regularization parameter becomes too small, the noise increases, which leads to overfitting. Ultimately, we see oversampling again when \(\lambda\) approaches 0.
Lets take a look on the spectra.
ind = [3,5,9,13];
plotSpektra(SO3F4(ind))
legend(['\lambda = ',num2str(reg(ind(1)))],['\lambda = ',num2str(reg(ind(2)))],['\lambda = ',num2str(reg(ind(3)))],['\lambda = ',num2str(reg(ind(4)))])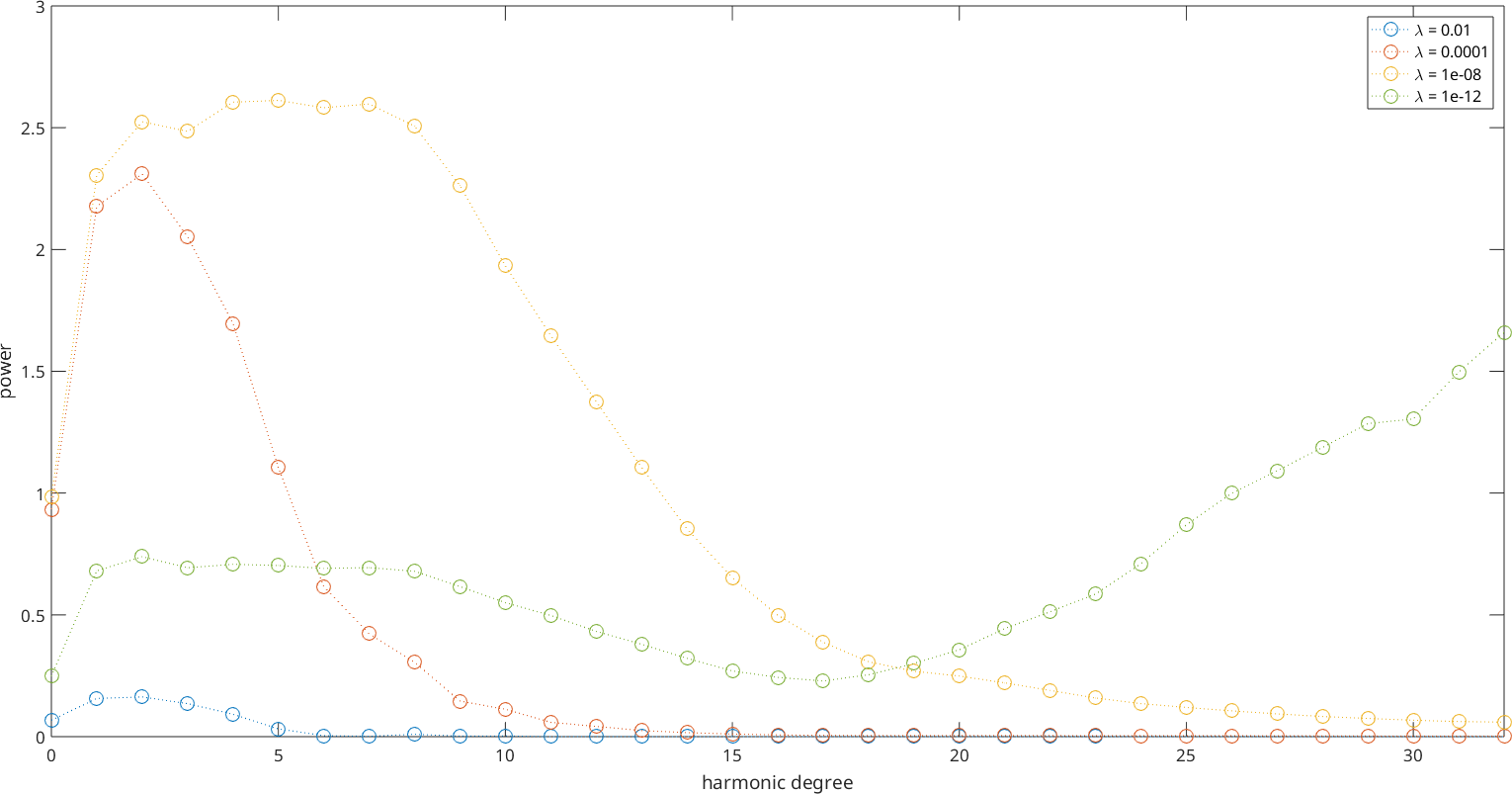
We can also choose another Sobolev index \(s=1\), which means that the Fourier coefficients should decrease more slowly.
SO3F5 = interp(ori, val,'harmonic','bandwidth',32,'regularization',0.001,'SobolevIndex',1)
% SO3F5 = SO3FunHarmonic.interpolate(ori,val,'bandwidth',32,'regularization',0.001,'SobolevIndex',1)
plot(SO3F5,'sigma')SO3F5 = SO3FunHarmonic (1 → y↑→x)
bandwidth: 32
weight: 0.98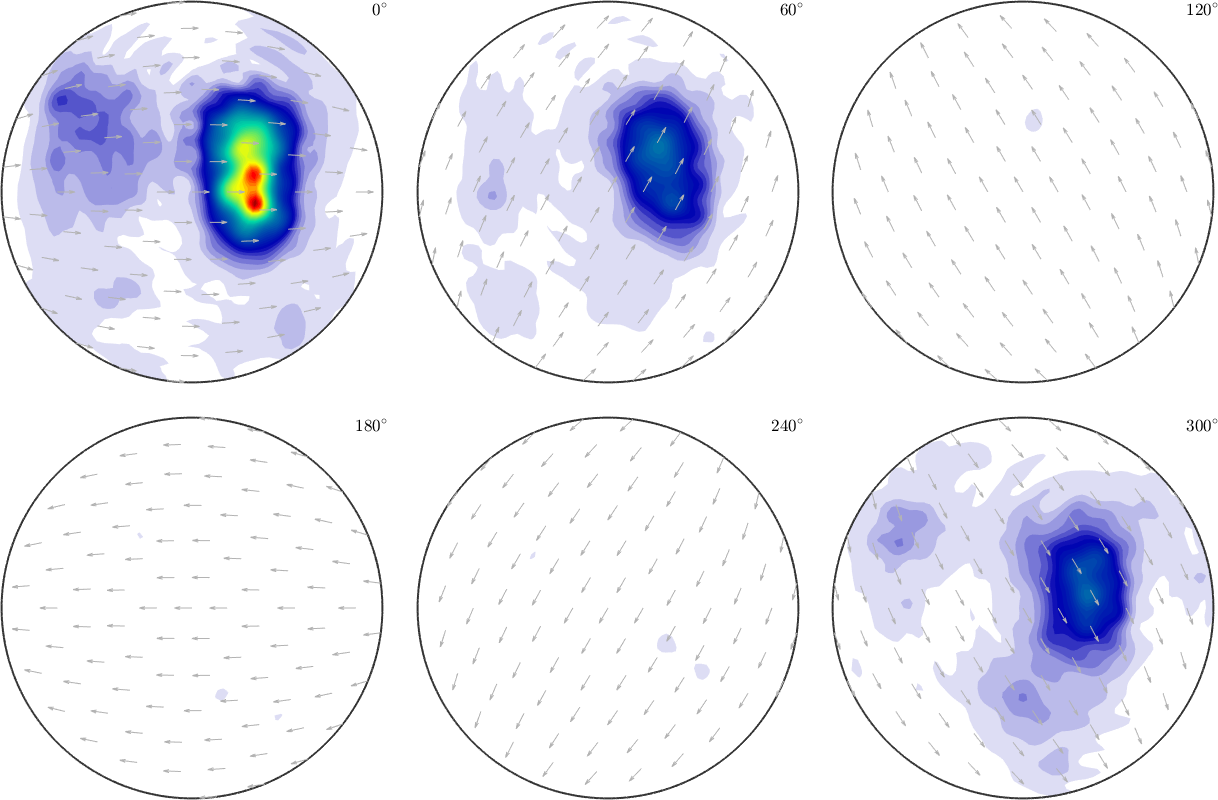
Note that we have to adapt the regularization parameter \(\lambda\).
LSQR-Parameters
Note that the lsqr solver from Matlab, which is used to minimize the least squares problem from above has some termination conditions. We can specify the method tolerance of lsqr with the option 'tol' (default 1e-3) and the maximum number of iterations by the option 'maxit' (default 100).
Thus we are able to control the precision of the result and computational time of the lsqr-method in the approximation process.
Moreover we obtain the lsqr parameters in a second output argument in the SO3FunHarmonic.interpolate-command.
% default Parameters
tic
[f1,p1] = SO3FunHarmonic.interpolate(ori, val);
toc
fprintf(['Number of iterations = ',num2str(p1{3}),'\n', ...
'Value of energy functional = ',num2str(norm(f1.eval(ori)-val)+5e-7*norm(f1,2)),'\n\n'])
% new termination conditions
tic
[f2,p2] = SO3FunHarmonic.interpolate(ori, val,'tol',1e-15);
toc
fprintf(['Number of iterations = ',num2str(p2{3}),'\n', ...
'Value of energy functional = ',num2str(norm(f2.eval(ori)-val)+5e-7*norm(f2,2)),'\n'])Elapsed time is 0.403489 seconds.
Number of iterations = 6
Value of energy functional = 100.132
Elapsed time is 1.908615 seconds.
Number of iterations = 36
Value of energy functional = 100.0924