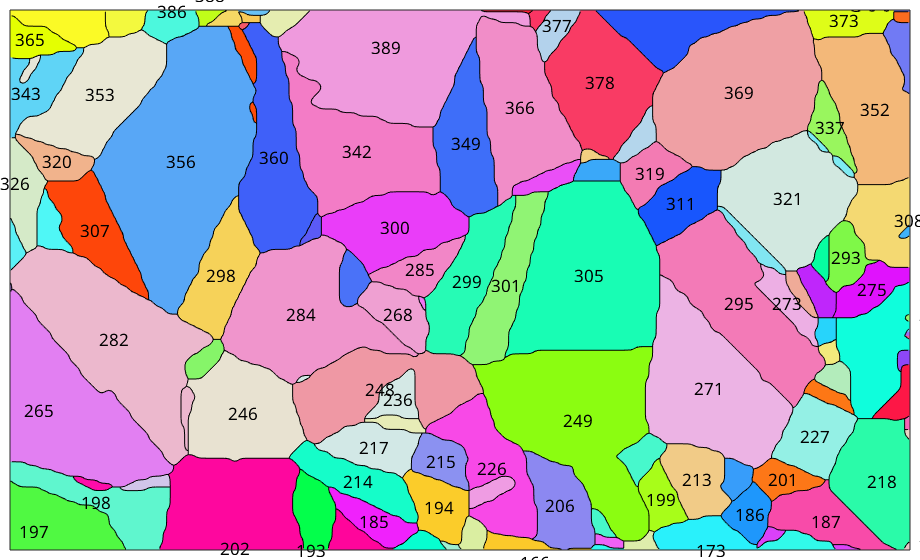
We start by importing some EBSD data and reconstructing some grains
% import a demo data set
mtexdata forsterite silent
% perform grain segmentation
[grains,ebsd.grainId,ebsd.mis2mean] = calcGrains(ebsd('indexed'),'minPixel',5);Phase maps
When using the plot command without additional argument the associated color is defined by color stored in the crystal symmetry for each phase
close all
plot(grains)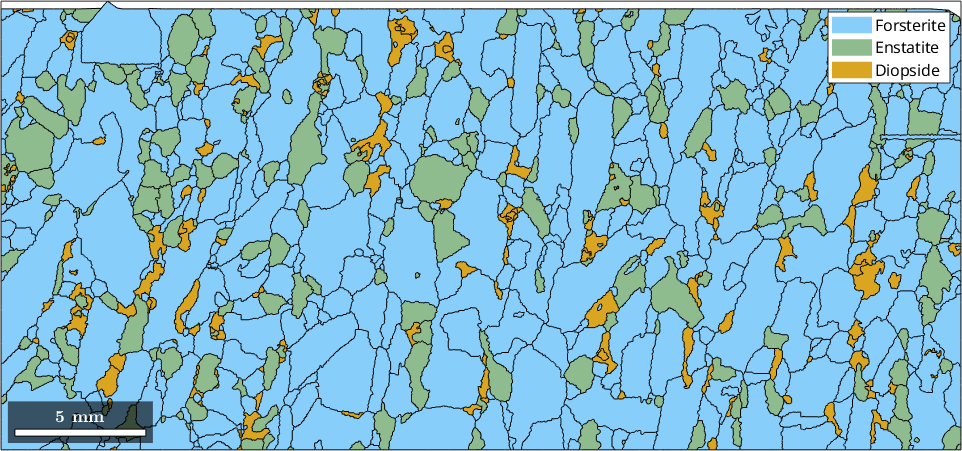
Accordingly, changing the color stored in the crystal symmetry changes the color in the map
grains('Fo').CS.color = str2rgb('salmon')
plot(grains)grains = grain2d (y↑→x)
Phase Grains Pixels Mineral Symmetry Crystal reference frame
1 438 151531 Forsterite mmm
2 207 25670 Enstatite mmm
3 166 7421 Diopside 12/m1 X||a*, Y||b*, Z||c
boundary segments: 35640 (1.6e+06 µm)
inner boundary segments: 285 (13093 µm)
triple points: 1399
Properties: meanRotation, GOS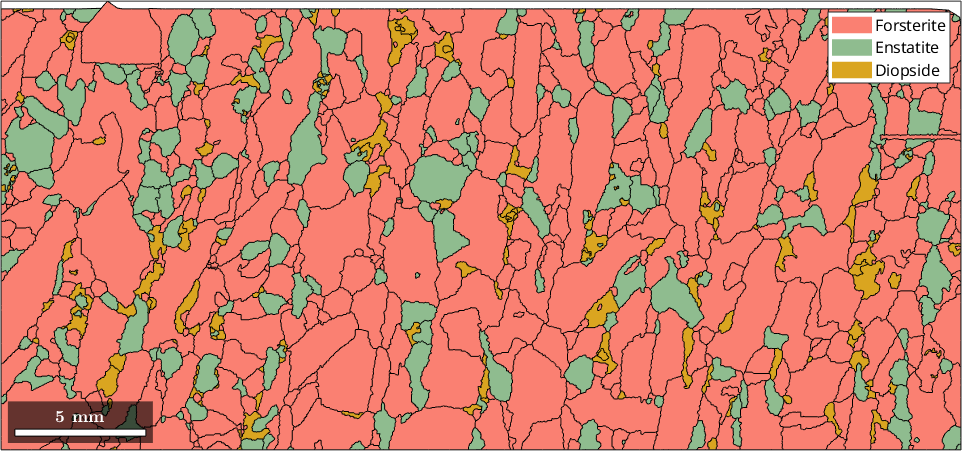
The color can also been specified directly by using the option FaceColor.
% detect the largest grain
[~,id] = max(grains.area);
% plot the grain in dark black with some transparency
hold on
plot(grains(id),'FaceColor','darkgray','FaceAlpha',0.7)
hold off
Orientation Maps
Coloring grains according to their mean orientations is very similar to EBSD maps colored by orientations. The most important thing is that the misorientation can only extracted from grains of the same phase.
% the implicit way
plot(grains('Fo'),grains('fo').meanOrientation)
This implicit way gives no control about how the color is computed from the meanorientation. When using the explicit way by defining a orientation to color map
% this defines a ipf color key
ipfKey = ipfColorKey(grains('Fo'));we can set the inverse pole figure direction and many other properties
ipfKey.inversePoleFigureDirection = xvector;
% compute the color from the meanorientation
color = ipfKey.orientation2color(grains('Fo').meanOrientation);
% and use them for plotting
plot(grains('fo'),color)
Plotting arbitrary properties
As we have seen in the previous section the plot command accepts as second argument any list of RGB values specifying a color. Instead of RGB values the second argument can also be a list of values which are then transformed by a colormap into color.
As an example we colorize the grains according to their aspect ratio.
plot(grains,grains.aspectRatio)
we see that we have a very elongated grain which makes it difficult to distinguish the aspect ration of the other grains. A solution for this is to specify the values of the aspect ration which should mapped to the top and bottom color of the colormap
setColorRange([1 5])
Colorizing circular properties
Sometimes the property we want to display is a circular, e.g., the direction of the grain elongation. In this case it is important to use a circular colormap which assign the same color to high values and low values. In the case of the direction of the grain elongation the angles 0 and 180 should get the same color since they represent the same direction.
% consider only elongated grains
alongated_grains = grains(grains.aspectRatio > 1.2);
% angle of the long axis to (1 0 0)
%omega = angle(alongated_grains.longAxis, vector3d.X, grains.N);
omega = mod(alongated_grains.longAxis.rho, pi);
% plot the direction
plot(alongated_grains,omega ./ degree,'micronbar','off')
% change the default colormap to a circular one
mtexColorMap HSV
% display the colormap
mtexColorbar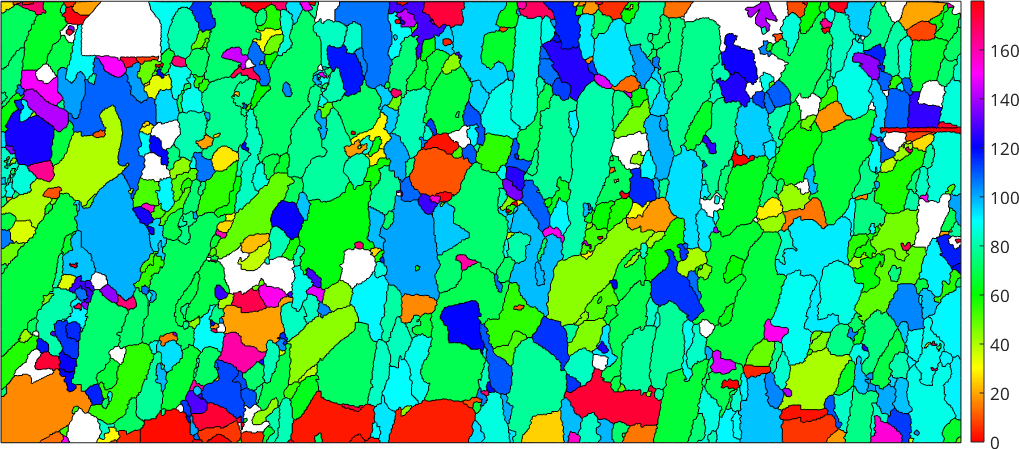
Plotting the orientation within a grain
In order to plot the orientations of EBSD data within certain grains one first has to extract the EBSD data that belong to the specific grains.
% let have a look at the biggest grain
[~,id] = max(grains.area)
% and select the corresponding EBSD data
ebsd_maxGrain = ebsd(ebsd.grainId == id)
% the previous command is equivalent to the more simpler
ebsd_maxGrain = ebsd(grains(id));id =
279
ebsd_maxGrain = EBSD (y↑→x)
Phase Orientations Mineral Color Symmetry Crystal reference frame
1 2683 (100%) Forsterite Salmon mmm
Properties: bands, bc, bs, error, mad, grainId, mis2mean
Scan unit : um
X x Y x Z : [16000, 19350] x [1550, 6800] x [0, 0]
Normal vector: (0,0,1)% compute the color out of the orientations
color = ipfKey.orientation2color(ebsd_maxGrain.orientations);
% plot it
plot(ebsd_maxGrain, color,'micronbar','off')
% plot the grain boundary on top
hold on
plot(grains(id).boundary,'linewidth',2)
hold off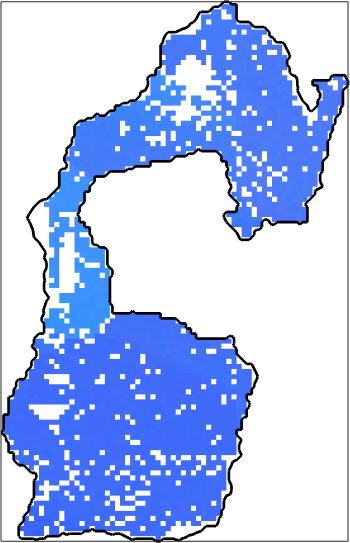
Visualizing directions
We may also visualize directions by arrows placed at the center of the grains using the command quiver.
% load some single phase data set
mtexdata csl
% compute and plot grains
[grains,ebsd.grainId] = calcGrains(ebsd,'minPixel',5);
grains = smooth(grains,5);
plot(grains,grains.meanOrientation,'micronbar','off','figSize','large','region',[50 300 100 250])
% next we want to visualize the direction of the 100 axis
dir = grains.meanOrientation * Miller(1,0,0,grains.CS);
% the length of the vectors should depend on the grain diameter
len = 0.25*grains.diameter;
% arrows are plotted using the command quiver. We need to switch of auto
% scaling of the arrow length
hold on
quiver(grains,len.*dir,'autoScale','off','color','black')
hold offebsd = EBSD (y↑→x)
Phase Orientations Mineral Color Symmetry Crystal reference frame
0 5 (0.0032%) notIndexed
-1 154107 (100%) iron LightSkyBlue m-3m
Properties: ci, error, iq
Scan unit : um
X x Y x Z : [0, 511] x [0, 300] x [0, 0]
Normal vector: (0,0,1)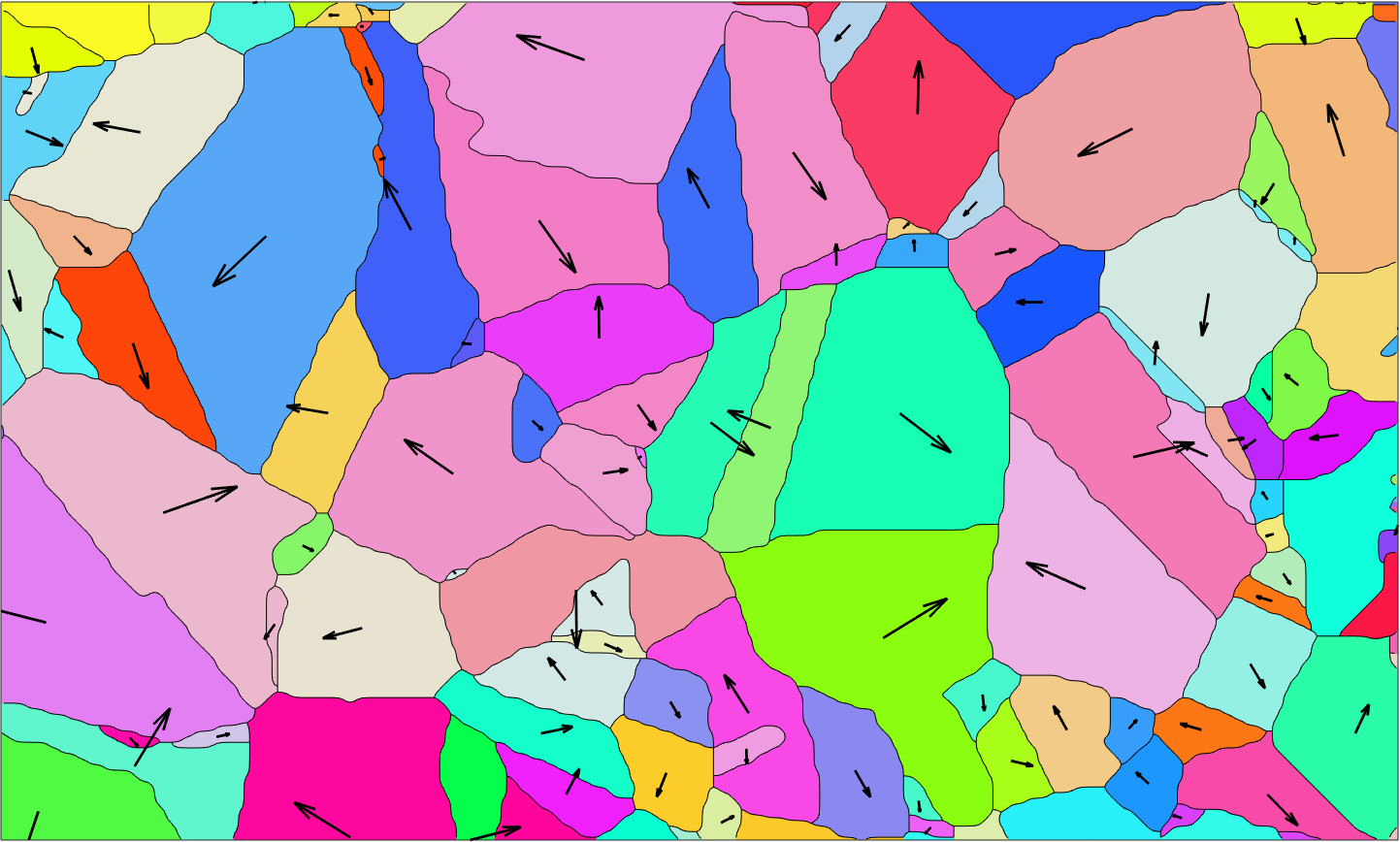
Labeling Grains
In the above example the vectors are centered at the centroids of the grains. We may also use the command text to display an arbitrary text on top of each grain.
% plot them
plot(grains,grains.meanOrientation,'micronbar','off','region',[50 300 100 250])
% only the big grains
big_grains = grains(grains.numPixel>100);
% plot on top their ids
text(big_grains,int2str(big_grains.id))