Birefringence

Birefringence edit page

Birefringence is the optical property of a material having a refractive index that depends on the polarization and propagation direction of light. It is one of the oldest methods to determine orientations of crystals in thin sections of rocks.

Import Olivine Data

In order to illustrate the effect of birefringence lets consider a olivine data set.

mtexdata olivine

% reconstruct grains
[grains,ebsd.grainId] = calcGrains(ebsd('indexed'),'minPixel',5);

% some data denoising
grains = smooth(grains,5);

F = halfQuadraticFilter;
ebsd = smooth(ebsd('indexed'),F,'fill',grains);

ebsd = EBSD (y↑→x)
 
 Phase  Orientations       Mineral         Color  Symmetry  Crystal reference frame
     1   44953 (90%)       olivine  LightSkyBlue       222                         
     2   1370 (2.8%)      Dolomite  DarkSeaGreen         3       X||a, Y||b*, Z||c*
     3   2311 (4.6%)     Enstatite     Goldenrod       222                         
     4   1095 (2.2%)  Chalcopyrite    LightCoral       422                         
 
 Properties: ci, fit, iq, sem_signal, unknown1, unknown2, unknown3, unknown4
 Scan unit : um
 X x Y x Z : [0, 888] x [-888, 0] x [0, 0]
 Normal vector: (0,0,-1)

% plot the olivine phase
plot(ebsd('olivine'),ebsd('olivine').orientations,'FaceAlpha',0.5);
hold on
plot(grains.boundary,'lineWidth',2)
hold off

% and on top the crystal shapes
bigGrains = grains(grains.numPixel > 100,'olivine');
cKey = ipfColorKey(bigGrains);
color = cKey.orientation2color(bigGrains.meanOrientation);
hold on
plot(bigGrains,0.8*crystalShape.olivine,'FaceColor',color,'faceAlpha',0.7)
hold off
drawNow(gcm,'final')

The refractive index tensor

The refractive index of a material describes the dependence of the speed of light with respect to the propagation direction and the polarization direction. In a linear world this relation ship is modeled by a symmetric rank 2 tensor - the so called refractive index tensor, which is usually given by it principle values: n_alpha, n_beta and n_gamma. In orthorhombic minerals such as olivine the principal values are parallel to the crystallographic axes. Care has to be applied when associating the principle values with the correct axes.

For Forsterite the principle refractive values are

n_alpha = 1.635; n_beta = 1.651; n_gamma = 1.670;

with the largest refractive index n_gamma being aligned with the a-axis, the intermediate index n_beta with the c-axis and the smallest refractive index n_alpha with the b-axis. Hence, the refractive index tensor for Forsterite takes the form

cs = ebsd('olivine').CS;
rI_Fo = refractiveIndexTensor(diag([ n_gamma  n_alpha  n_beta]),cs)

rI_Fo = refractiveIndexTensor (olivine)
  rank: 2 (3 x 3)
 
  1.67     0     0
     0 1.635     0
     0     0 1.651

For Fayalite the principle refractive values

n_alpha = 1.82; n_beta = 1.869; n_gamma = 1.879;

are aligned to the crystallographic axes in an analogous way. Which leads to the refractive index tensor

rI_Fa = refractiveIndexTensor(diag([ n_gamma  n_alpha  n_beta]),cs)

rI_Fa = refractiveIndexTensor (olivine)
  rank: 2 (3 x 3)
 
 1.879     0     0
     0  1.82     0
     0     0 1.869

The refractive index of composite materials like Olivine can now be modeled as the weighted sum of the of the refractive index tensors of Forsterite and Fayalite. Lets assume that the relative Forsterite content (atomic percentage) is given my

XFo = 0.86; % 86 percent Forsterite

Then is refractive index tensor becomes

rI = XFo*rI_Fo + (1-XFo) * rI_Fa

rI = refractiveIndexTensor (olivine)
  rank: 2 (3 x 3)
 
 1.6993      0      0
      0 1.6609      0
      0      0 1.6815

Birefringence

The birefringence describes the difference n in diffraction index between the fastest polarization direction pMax and the slowest polarization direction pMin for a given propagation direction vprop.

% lets define a propagation direction
vprop = Miller(1,1,1,cs);

% and compute the birefringence
[dn,pMin,pMax] = rI.birefringence(vprop)

dn =
    0.0245
 
pMin = vector3d (y↑→x)
        x         y         z
  0.19057 -0.932509  0.306774
 
pMax = vector3d (y↑→x)
          x         y         z
  -0.650059  0.114293  0.751239

If the polarization direction is omitted the results are spherical functions which can be easily visualized.

% compute the birefringence as a spherical function
[dn,pMin,pMax] = rI.birefringence

% plot it
plot3d(dn,'complete')
mtexColorMap parula
mtexColorbar

% and on top of it the polarization directions
hold on
quiver3(pMin,'color','white')
quiver3(pMax)
hold off

dn = S2FunHarmonicSym (olivine)
  bandwidth: 48
  isReal: true
 
 
pMin = S2AxisFieldHarmonic
 bandwidth: 48
 
pMax = S2AxisFieldHarmonic
 bandwidth: 48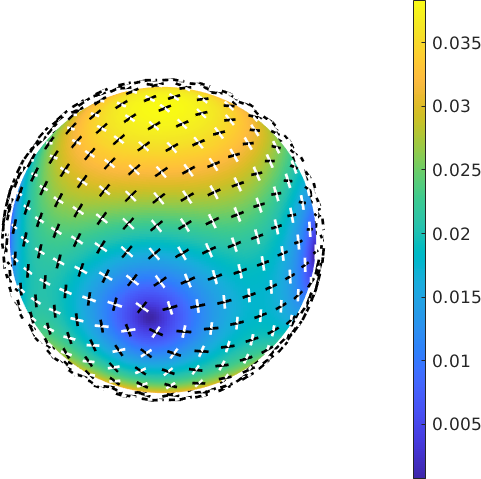

The Optical Axis

The optical axes are all directions where the birefringence is zero

% compute the optical axes
vOptical = rI.opticalAxis

% and check the birefringence is zero
rI.birefringence(vOptical)

% annotate them to the birefringence plot
hold on
vOptical.antipodal = false;
arrow3d([vOptical,-vOptical] ,'facecolor','red')
hold off

vOptical = vector3d (y↑→x)
 size: 1 x 2
 antipodal: true
          x         y         z
  -0.680045  0.733171         0
   0.680045  0.733171         0
ans =
   1.0e-15 *
    0.4441
    0.4441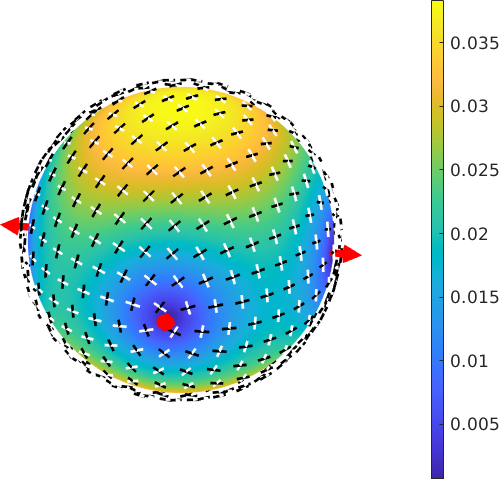

Spectral Transmission

If white light with a certain polarization is transmitted though a crystal with isotropic refractive index the light changes wavelength and hence appears colored. The resulting color depending on the propagation direction, the polarization direction and the thickness can be computed by

vprop = Miller(1,1,1,cs);
thickness = 30000;
p =  Miller(-1,1,0,cs);
rgb = rI.spectralTransmission(vprop,thickness,'polarizationDirection',p)

rgb =
    0.3635    0.7380    0.6967

Effectively, the rgb value depend only on the angle tau between the polarization direction and the slowest polarization direction pMin. Instead of the polarization direction this angle may be specified directly

rgb = rI.spectralTransmission(vprop,thickness,'tau',30*degree)

rgb =
    0.3128    0.6350    0.5994

If the angle tau is fixed and the propagation direction is omitted as input MTEX returns the rgb values as a spherical function. Lets plot these functions for different values of tau.

newMtexFigure('layout',[1,3]);

mtexTitle('\(\tau = 15^{\circ}\)')
plot(rI.spectralTransmission(thickness,'tau',15*degree),'rgb')

nextAxis
mtexTitle('\(\tau = 30^{\circ}\)')
plot(rI.spectralTransmission(thickness,'tau',30*degree),'rgb')

nextAxis
mtexTitle('\(\tau = 45^{\circ}\)')
plot(rI.spectralTransmission(thickness,'tau',45*degree),'rgb')

drawNow(gcm,'figSize','normal')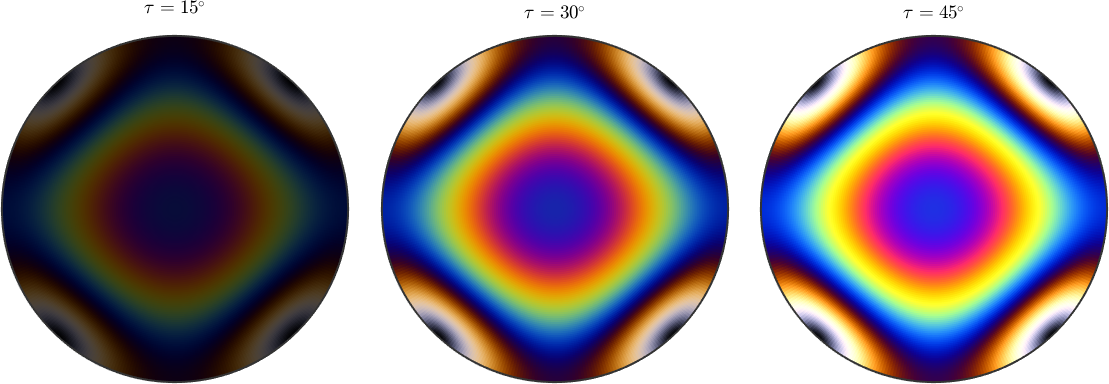

Usually, the polarization direction is chosen at angle phi = 90 degree of the analyzer. The following plots demonstrate how to change this angle

newMtexFigure('layout',[1,3]);

mtexTitle('\(\tau = 15^{\circ}\)')
plot(rI.spectralTransmission(thickness,'tau',45*degree,'phi',30*degree),'rgb')

nextAxis
mtexTitle('\(\tau = 30^{\circ}\)')
plot(rI.spectralTransmission(thickness,'tau',45*degree,'phi',60*degree),'rgb')

nextAxis
mtexTitle('\(\tau = 45^{\circ}\)')
plot(rI.spectralTransmission(thickness,'tau',45*degree,'phi',90*degree),'rgb')

drawNow(gcm,'figSize','normal')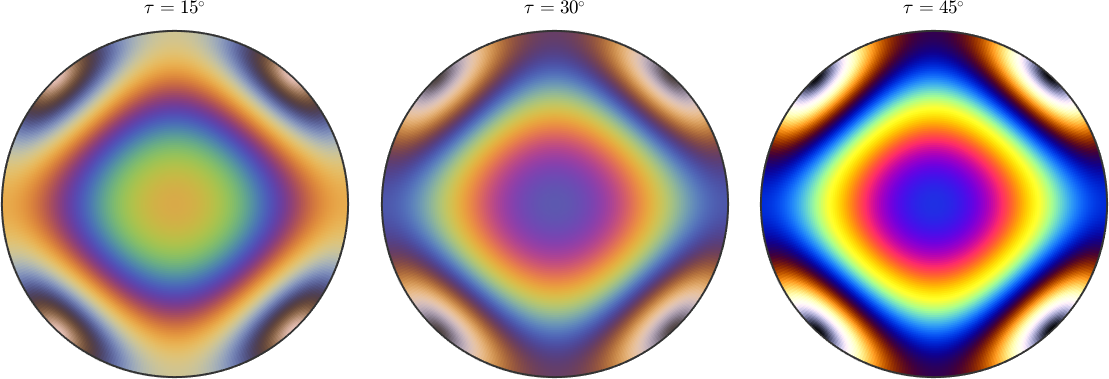

Spectral Transmission at Thin Sections

All the above computations have been performed in crystal coordinates. However, in practical applications the direction of the polarizer as well as the propagation direction are given in terms of specimen coordinates.

% the propagation direction
vprop = vector3d.Z;

% the direction of the polarizer
polarizer = vector3d.X;

% the thickness of the thin section
thickness = 22800;

As usual we have two options: Either we transform the refractive index tensor into specimen coordinates or we transform the polarization direction and the propagation directions into crystal coordinates. Lets start with the first option:

% extract the olivine orientations
ori = ebsd('olivine').orientations;

% transform the tensor into a list of tensors with respect to specimen
% coordinates
rISpecimen = ori * rI;

% compute RGB values
rgb = rISpecimen.spectralTransmission(vprop,thickness,'polarizationDirection',polarizer);

% colorize the EBSD maps according to spectral transmission
plot(ebsd('olivine'),rgb)

and compare it with option two:

% transform the propagation direction and the polarizer direction into a list
% of directions with respect to crystal coordinates
vprop_crystal = ori \ vprop;
polarizer_crystal = ori \ polarizer;

% compute RGB values
rgb = rI.spectralTransmission(vprop_crystal,thickness,'polarizationDirection',polarizer_crystal);

% colorize the EBSD maps according to spectral transmission
plot(ebsd('olivine'),rgb)

Spectral Transmission as a color key

The above computations can be automated by defining a spectral transmission color key.

% define the colorKey
colorKey  = spectralTransmissionColorKey(rI,thickness);

% the following are the defaults and can be omitted
colorKey.propagationDirection = vector3d.Z;
colorKey.polarizer = vector3d.X;
colorKey.phi = 90 * degree;

% compute the spectral transmission color of the olivine orientations
rgb = colorKey.orientation2color(ori);

plot(ebsd('olivine'), rgb)

As usual we me visualize the color key as a colorization of the orientation space, e.g., by plotting it in sigma sections:

plot(colorKey,'sigma')

Circular Polarizer

In order to simulate we a circular polarizer we simply set the polarizer direction to empty, i.e.

colorKey.polarizer = [];

% compute the spectral transmission color of the olivine orientations
rgb = colorKey.orientation2color(ori);

plot(ebsd('olivine'), rgb)

Illustrating the effect of rotating polarizer and analyzer simultaneously

colorKey.polarizer = vector3d.X;
figure
plotHandle = plot(ebsd('olivine'),colorKey.orientation2color(ori),'micronbar','off');
hold on
plot(grains.boundary,'lineWidth',2)
hold off
textHandle = text(750,50,[num2str(0,'%10.1f') '\circ'],'fontSize',15,...
  'color','w','backGroundColor', 'k');

% define the step size in degree
stepSize = 2.5;

for omega = 0:stepSize:90-stepSize

  % update polarization direction
  colorKey.polarizer = rotate(vector3d.X, omega * degree);

  % update rgb values
  plotHandle.FaceVertexCData = colorKey.orientation2color(ori);

  % update text
  textHandle.String = [num2str(omega,'%10.1f') '\circ'];

  drawnow

end