Let us first begin with some constructed ODFs to be analyzed below
A bimodal ODF:
cs = crystalSymmetry('mmm');
odf1 = unimodalODF(orientation.byEuler(0,0,0,cs)) + ...
unimodalODF(orientation.byEuler(30*degree,0,0,cs))odf1 = SO3FunRBF (mmm → y↑→x)
multimodal components
kernel: de la Vallee Poussin, halfwidth 10°
center: 2 orientations
Bunge Euler angles in degree
phi1 Phi phi2 weight
0 0 0 1
30 0 0 1A fibre ODF:
f001_x = fibre(Miller(0,0,1,cs),xvector)
odf2 = fibreODF(f001_x)f001_x = fibre (mmm → y↑→x)
h || r: (001) || (1,0,0)
odf2 = SO3FunCBF (mmm → y↑→x)
kernel: de la Vallee Poussin, halfwidth 10°
fibre : (001) || 1,0,0
weight: 1An ODF estimated from diffraction data
mtexdata dubna
odf3 = calcODF(pf,'resolution',5*degree,'zero_Range')pf = PoleFigure (y↑→x)
crystal symmetry : Quartz (321, X||a*, Y||b, Z||c*)
h = (02-21), r = 72 x 19 points
h = (10-10), r = 72 x 19 points
h = (10-11)(01-11), r = 72 x 19 points
h = (10-12), r = 72 x 19 points
h = (11-20), r = 72 x 19 points
h = (11-21), r = 72 x 19 points
h = (11-22), r = 72 x 19 points
odf3 = SO3FunRBF (Quartz → y↑→x)
multimodal components
kernel: de la Vallee Poussin, halfwidth 5°
center: 19848 orientations, resolution: 5°
weight: 1Modal Orientations
The modal orientation of an ODF is the crystallographic preferred orientation ori_pref of the texture. It is characterized as the maximum of the ODF. In MTEX it is returned as the second output argument of the command max
[~,ori_pref] = max(odf3)ori_pref = orientation (Quartz → y↑→x)
Bunge Euler angles in degree
phi1 Phi phi2
133.047 34.5158 207.16Lets mark this preferred orientation in the pole figures
plotPDF(odf3,pf.allH,'antipodal','superposition',pf.c);
annotate(ori_pref,'marker','s','MarkerFaceColor','black')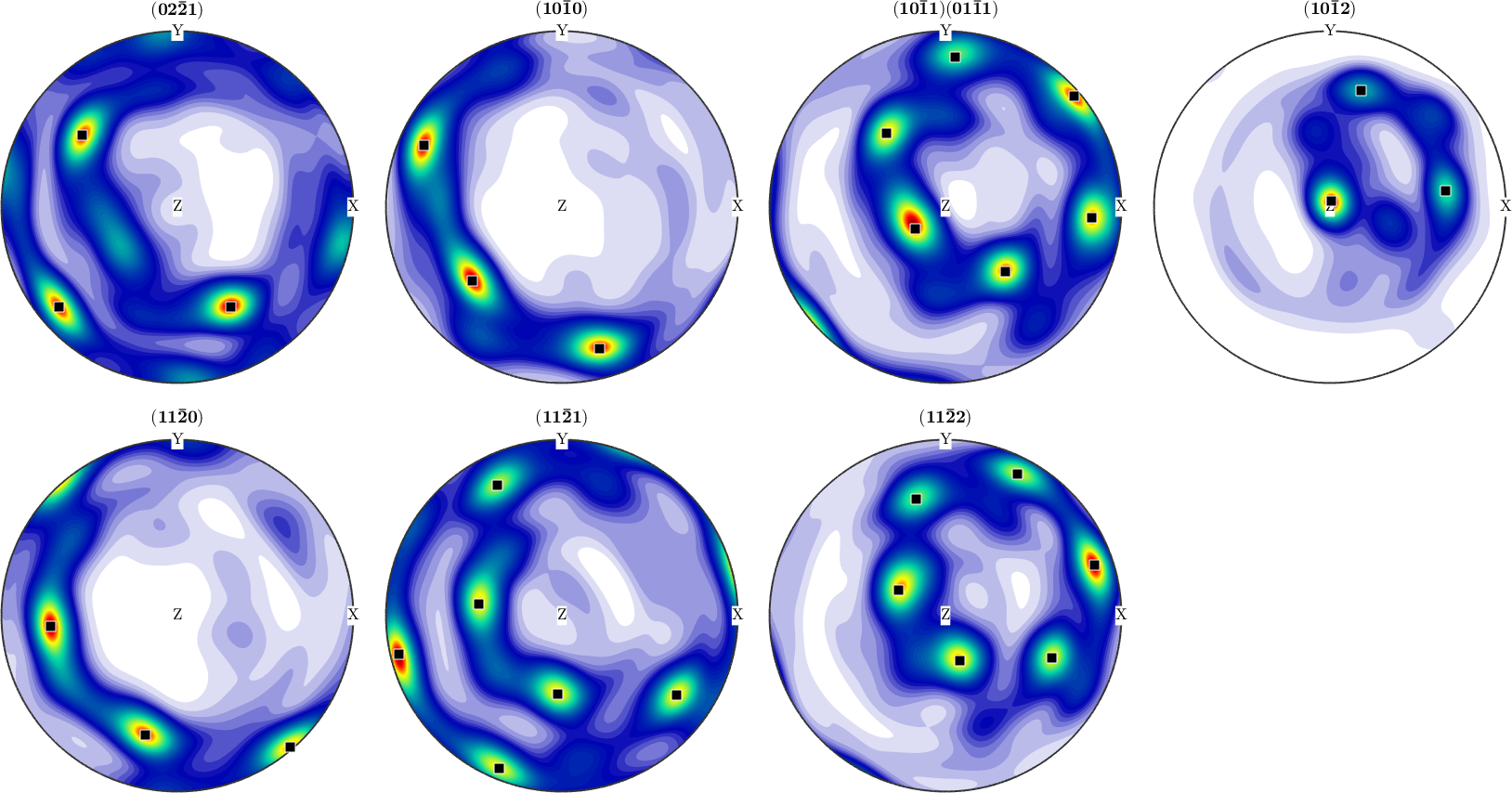
Texture Characteristics
Texture characteristics are used for a rough classification of ODFs into sharp and weak ones. The two most common texture characteristics are the entropy and the texture index. The texture index of an ODF \(f\) is defined as:
\[ t = \int_{SO(3)} f({R})^2 dR\]
We may either compute this integral using the command sum directly by
t = mean(odf1.*odf1)t =
288.5696or, more efficiently, by the command norm
t = norm(odf1)^2t =
288.6802The entropy of an ODF \(f\) is defined as:
\[ H = - \int_{SO(3)} f({R}) \ln f({R}) dR\]
H = entropy(odf2)H =
-2.8402Volume Portions
Volume portions describes the relative volume of crystals having a certain orientation. The relative volume of crystals having a orientation close to a given orientation is computed by the command volume and the relative volume of crystals having a orientation close to a given fibre is computed by the command fibreVolume
The relative volume in percent of crystals with misorientation maximum 30 degree from the preferred orientation ori_pref:
V1 = volume(odf3, ori_pref, 30*degree) * 100V1 =
33.8649The relative volume of crystals with misorientation maximum 20 degree from the preferred fibre in percent:
V2 = volume(odf2,f001_x,20*degree) * 100V2 =
95.1633