Pole Figure Tutorial

Pole Figure Tutorial edit page

This tutorial explains the basic concepts for ananyzing x-ray, synchrotron and neutron diffraction pole figure data.

Import pole figure diffraction data

Click on Import pole figure data to start the import wizard which is a GUI leading you through the import of pole figure data. After finishing the wizard you will end up with a script similar to the following one.

% This script was automatically created by the import wizard. You should
% run the whole script or parts of it in order to import your data. There
% is no problem in making any changes to this script.
%
% *Specify Crystal and Specimen Symmetries*

% crystal symmetry for this ZnCuTi data is hexagonal.  Here we define the crystallographic unit cell and how it relates to cartesian xyz axes.
CS = crystalSymmetry('6/mmm', [2.633 2.633 4.8], 'X||a*', 'Y||b', 'Z||c');

% specimen symmetry tells MTEX if a certain symmetry should be present in the plotted pole figures.  The command used here selects triclinic, the most flexible option.
SS = specimenSymmetry('1');

% plotting convention
setMTEXpref('xAxisDirection','north');
setMTEXpref('zAxisDirection','outOfPlane');

Specify File Names

% path to files downloaded with the MTEX package
pname = [mtexDataPath filesep 'PoleFigure' filesep 'ZnCuTi' filesep];

% which pole figure files are to be imported
fname = {...
  [pname 'ZnCuTi_Wal_50_5x5_PF_002_R.UXD'],...
  [pname 'ZnCuTi_Wal_50_5x5_PF_100_R.UXD'],...
  [pname 'ZnCuTi_Wal_50_5x5_PF_101_R.UXD'],...
  [pname 'ZnCuTi_Wal_50_5x5_PF_102_R.UXD'],...
  };

% defocusing correction to compensate for the equipment-dependent loss of intensity at certain angles.
fname_def = {...
  [pname 'ZnCuTi_defocusing_PF_002_R.UXD'],...
  [pname 'ZnCuTi_defocusing_PF_100_R.UXD'],...
  [pname 'ZnCuTi_defocusing_PF_101_R.UXD'],...
  [pname 'ZnCuTi_defocusing_PF_102_R.UXD'],...
  };

Specify Miller Indices

% These correspond to the files loaded, in order.
h = { ...
  Miller(0,0,2,CS),...
  Miller(1,0,0,CS),...
  Miller(1,0,1,CS),...
  Miller(1,0,2,CS),...
  };

Import the Data

% create a Pole Figure variable containing the data
pf = PoleFigure.load(fname,h,CS,SS,'interface','uxd');

% create a defocusing pole figure variable
pf_def = PoleFigure.load(fname_def,h,CS,SS,'interface','uxd');

% correct data by applying the defocusing compensation
pf = correct(pf,'def',pf_def);

After running the script the variable pf is created which contains all information about the pole figure data. You may plot the data using the command plot

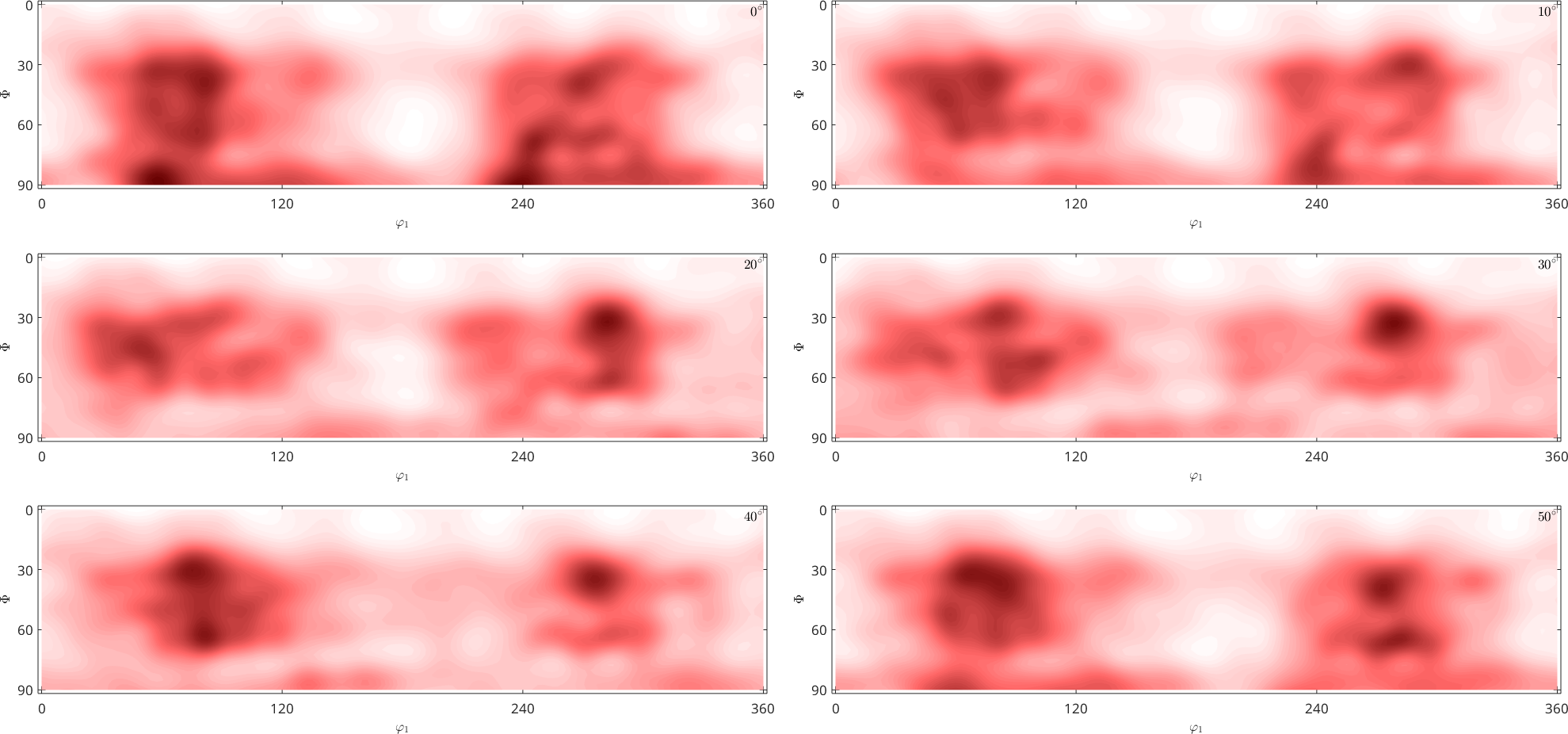
plot(pf)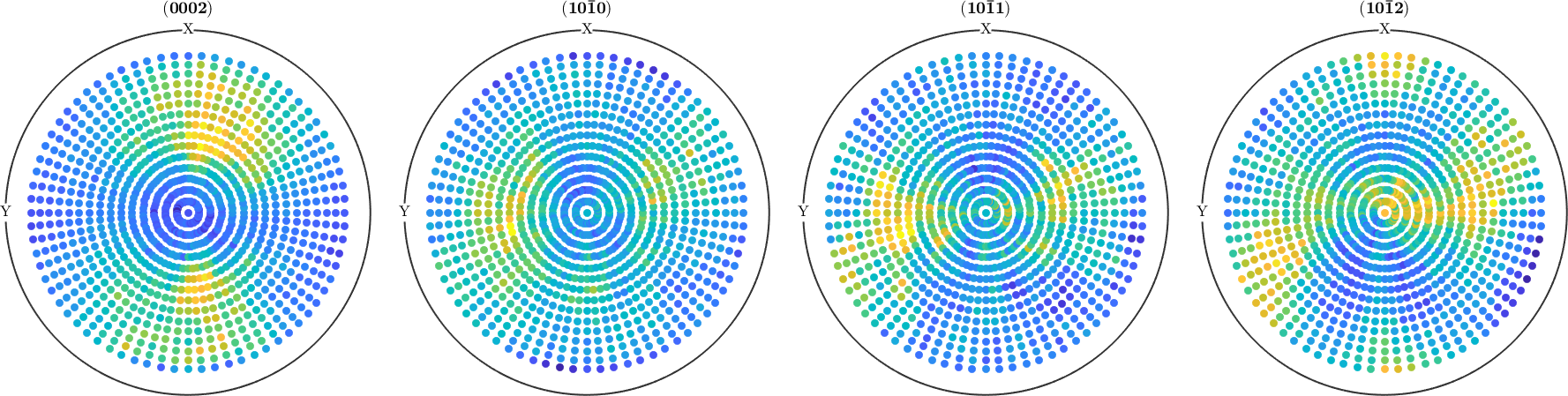

By default pole figures are plotted as intensity-colored dots for every data point. There are many options to specify the way pole figures are plotted in MTEX. Have a look at the plotting section for more information.

After import make sure that the Miller indices are correctly assigned to the pole figures and that the alignment of the specimen coordinate system, i.e., X, Y, Z is correct. In case of outliers or misaligned data, you may want to correct your raw data. Have a look at the correction section for further information. MTEX offers several methods correcting pole figure data, e.g.

rotating pole figures
scaling pole figures
finding outliers
removing specific measurements
superposing pole figures

As an example we set all negative intensities to zero

pf(pf.intensities<0) = 0;
plot(pf)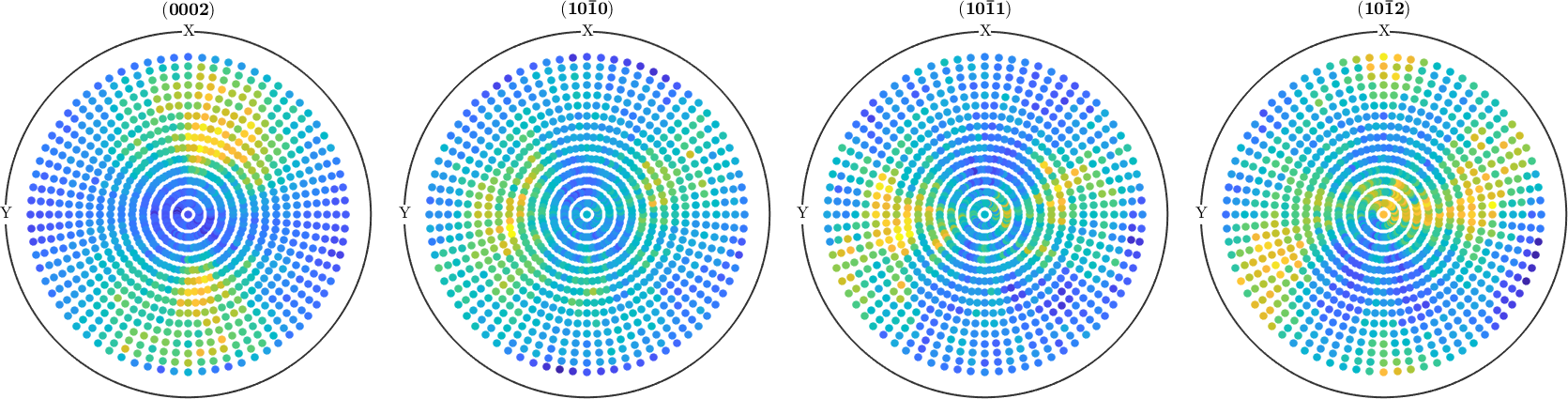

ODF Estimation

Once your data is in good shape, i.e. defocusing correction has been done and few outliers are left you can reconstruct an ODF out of this data. This is done by the command calcODF.

odf = calcODF(pf,'silent')

odf = SO3FunRBF (6/mmm → xyz)
 
  uniform component
  weight: 0.54
 
  multimodal components
  kernel: de la Vallee Poussin, halfwidth 5°
  center: 9924 orientations, resolution: 5°
  weight: 0.46

Note that reconstructing an ODF from pole figure data is a severely ill- posed problem, i.e., it does not provide a unique solution. A more through discussion on the ambiguity of ODF reconstruction from pole figure data can be found here. As a rule of thumb: the more pole figures you have and the more consistent your pole figure data the better your reconstructed ODF will be.

To check how well your reconstructed ODF fits the measured pole figure data use

figure;plotPDF(odf,pf.h)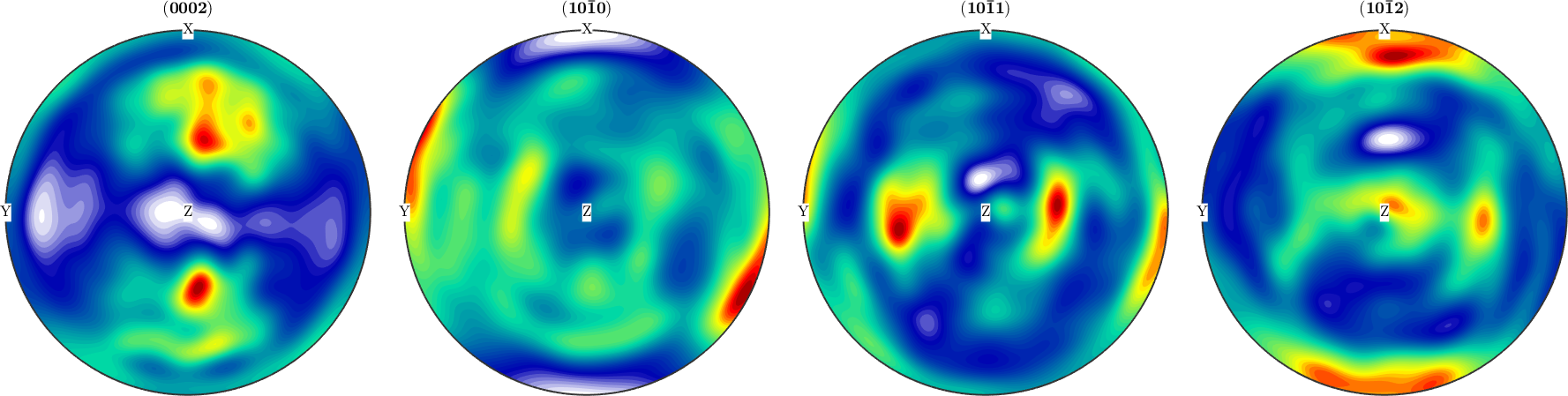

Compare the recalculated pole figures with the measured data. A quantitative measure for the fitting is the so called RP value. They can be computed for each imported pole figure with

calcError(odf,pf)

ans =
    0.0412    0.0416    0.0548    0.0418

In the case of a bad fit, you may want to tweak the reconstruction algorithm. See here for more information.

Visualize the ODF

Finally one can plot the resulting ODF

plot(odf)
mtexColorMap LaboTeX