Elastic waves traveling through an anisotropic medium do not propagate with the same speed in every direction. In this section we explain how MTEX derives from an elastic stiffness tensor the direction dependent velocities of the P-wave and of the two S-waves, together with their polarization directions, how these quantities are visualized and which anisotropy measures are commonly derived from them.
Import an Elasticity Tensor
Let us start by importing the elastic stiffness tensor of an Olivine crystal in reference orientation from a file.
fname = fullfile(mtexDataPath,'tensor','Olivine1997PC.GPa');
cs = crystalSymmetry('mmm',[4.7646 10.2296 5.9942],'mineral','Olivin');
C = stiffnessTensor.load(fname,cs)C = stiffnessTensor (Olivin)
unit: GPa
rank: 4 (3 x 3 x 3 x 3)
tensor in Voigt matrix representation:
320.5 68.2 71.6 0 0 0
68.2 196.5 76.8 0 0 0
71.6 76.8 233.5 0 0 0
0 0 0 64 0 0
0 0 0 0 77 0
0 0 0 0 0 78.7The Density
Wave velocities do not only depend on the stiffness tensor but also on the density \(\rho\) of the material. For Olivine it is about 3.355 g/cm\(^3\). Since the density is required by almost every command in this section it is most convenient to store it directly within the stiffness tensor
rho = 3.355;
C = addOption(C,'density',rho)C = stiffnessTensor (Olivin)
unit : GPa
density: 3.355
rank : 4 (3 x 3 x 3 x 3)
tensor in Voigt matrix representation:
320.5 68.2 71.6 0 0 0
68.2 196.5 76.8 0 0 0
71.6 76.8 233.5 0 0 0
0 0 0 64 0 0
0 0 0 0 77 0
0 0 0 0 0 78.7Alternatively, the density may be passed as the option 'density' when the tensor is defined, e.g. stiffnessTensor(M,cs,'density',rho), or as a trailing argument to the individual commands.
The Christoffel Equation
Consider a plane wave with propagation direction \(\vec n\), phase velocity \(v\) and polarization direction \(\vec p\), i.e., a displacement field of the form
\[ \vec u(\vec x,t) = \vec p \, f(\vec n \cdot \vec x - v t). \]
Substituting this ansatz into the equation of motion \(\rho \, \partial_t^2 u_i = \partial_j \sigma_{ij}\) together with Hooke's law \(\sigma_{ij} = C_{ijkl}\varepsilon_{kl}\) results in the Christoffel equation
\[ C_{ijkl} n_j n_l \, p_k = \rho v^2 p_i. \]
In other words, the admissible polarization directions \(\vec p\) are the eigenvectors of the symmetric rank two tensor
\[ E_{ik}(\vec n) = C_{ijkl} n_j n_l \]
and the corresponding eigenvalues are the wave moduli \(\rho v^2\).
The Christoffel Tensor
The tensor \(E(\vec n)\) is called the Christoffel tensor and is computed for a specific propagation direction \(\vec n\) by the command ChristoffelTensor
T = ChristoffelTensor(C,vector3d.X)T = ChristoffelTensor (Olivin)
rank: 2 (3 x 3)
320.5 0 0
0 78.7 0
0 0 77The Christoffel tensor is symmetric as a consequence of the symmetry \(C_{ijkl} = C_{klij}\) of the elastic constants. Hence, its three eigenvalues are real and the three eigenvectors are perpendicular to each other. Since the stiffness tensor is positive definite the eigenvalues are, moreover, positive and therefore correspond to three real wave speeds. Let us compute this eigenvalue decomposition
[p,lambda] = eig(T)p = vector3d (y↓→x)
size: 3 x 1
antipodal: true
x y z
0 0 1
0 1 0
1 0 0
lambda =
77.0000
78.7000
320.5000MTEX returns the eigenvalues in ascending order. Dividing them by the density and taking the square root gives the three wave velocities in km/s
v = sqrt(lambda ./ rho)v =
4.7907
4.8433
9.7739The largest of them belongs to the P-wave, i.e., the wave whose polarization direction is closest to the propagation direction, while the two smaller ones belong to the fast and the slow S-wave. Note that for the direction vector3d.X, which is a symmetry axis of our Olivine crystal, the polarization directions coincide with the coordinate axes and the P-wave is polarized exactly parallel to the propagation direction.
Elastic Wave Velocities
Instead of decomposing the Christoffel tensor by hand the command velocity performs all these steps at once and directly sorts the result into P-wave, fast S-wave and slow S-wave
[vp,vs1,vs2,pp,ps1,ps2] = velocity(C,vector3d.X)vp =
9.7739
vs1 =
4.8433
vs2 =
4.7907
pp = vector3d (y↓→x)
antipodal: true
x y z
1 0 0
ps1 = vector3d (y↓→x)
antipodal: true
x y z
0 1 0
ps2 = vector3d (y↓→x)
antipodal: true
x y z
0 0 1Here vp, vs1, vs2 are the velocities of the P-wave, the fast S-wave and the slow S-wave, while pp, ps1, ps2 are the corresponding polarization directions, i.e., the directions the particles vibrate in. Since a polarization direction is only defined up to sign it is returned as an axis.
The command accepts arbitrary lists of propagation directions
x = [vector3d.X,vector3d.Y,vector3d.Z]
vp = velocity(C,x)x = vector3d (y↓→x)
size: 1 x 3
x y z
1 0 0
0 1 0
0 0 1
vp =
9.7739 7.6531 8.3425Velocities as Spherical Functions
If the propagation direction is omitted altogether the wave velocities are computed for the entire sphere and returned as spherical functions
[vp,vs1,vs2,pp,ps1,ps2] = velocity(C)vp = S2FunTri (y↓→x)
vertices: 18338 x 1
vs1 = S2FunTri (y↓→x)
vertices: 18338 x 1
vs2 = S2FunTri (y↓→x)
vertices: 18338 x 1
pp = S2AxisFieldTri
vertices: 18338 x 1
ps1 = S2AxisFieldTri
vertices: 18338 x 1
ps2 = S2AxisFieldTri
vertices: 18338 x 1As output we obtain three spherical functions vp, vs1 and vs2 representing the velocities of P, and fast and slow S-waves respectively in dependency of the propagation direction. The remaining three output variables pp, ps1, ps2 are spherical vector fields representing the polarization directions of these wave as functions of the propagation direction.
Being ordinary spherical functions they may be evaluated at any direction
vp.eval(vector3d.X)ans =
9.7735By default the velocities are sampled on a triangulated grid and interpolated in between, which explains the small deviation from the exact value computed above. Passing the option 'harmonic' returns harmonic expansions instead. These are smooth, respect the crystal symmetry exactly and are the better choice for three dimensional plots
vpHarm = velocity(C,'harmonic')vpHarm = S2FunHarmonicSym (Olivin)
bandwidth: 48
antipodal: trueVisualizing the Wave Velocities
In order to visualize these quantities, there are several possibilities. Let us first plot the direction dependent wave speed of the p-wave
setMTEXpref('defaultColorMap',blue2redColorMap);
plot(vp,'complete','upper')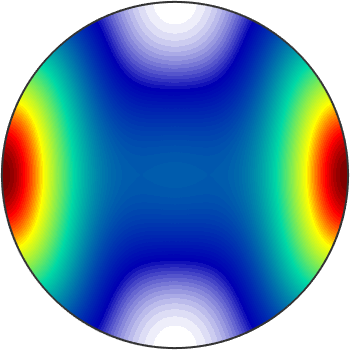
Next, we plot on the top of this plot the p-wave polarization direction.
hold on
plot(pp)
hold off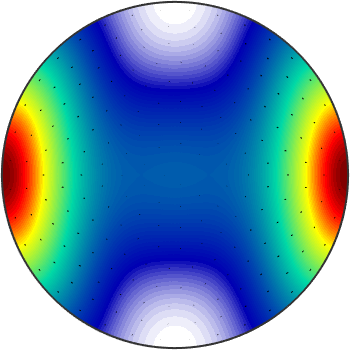
Note how the polarization of the P-wave stays close to the propagation direction it is plotted at - the P-wave is almost, but not exactly, a longitudinal wave.
Shear Wave Splitting
We may even compute with these spherical functions as with ordinary values. E.g. to visualize the speed difference between the s1 and s2 waves we do.
plot(vs1-vs2,'complete','upper')
hold on
plot(ps1)
hold off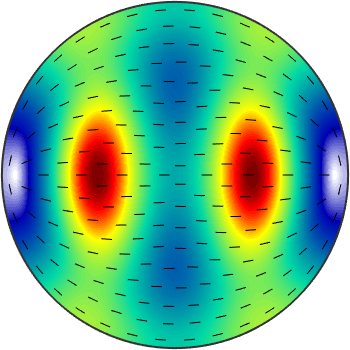
This difference is the reason for shear wave splitting: an S-wave entering an anisotropic medium is split into a fast and a slow component which are polarized perpendicular to each other and arrive with a delay. The line segments above show the polarization ps1 of the fast S-wave, which is the quantity a seismologist measures. Directions where the difference vanishes are the acoustic axes of the crystal - there both S-waves travel with the same speed and no splitting occurs.
Anisotropy Measures
The relative velocity variation of a wave is usually reported as a percentage of its mean velocity. For the P-wave this gives
[maxVp,maxPos] = max(vp);
[minVp,minPos] = min(vp);
AVp = 200*(maxVp-minVp)./(maxVp+minVp)AVp =
24.3329Let us mark the corresponding fastest and slowest propagation directions in the plot
plot(vp,'complete','upper')
hold on
plot(maxPos(1),'Marker','s','MarkerSize',10,'MarkerFaceColor','k','MarkerEdgeColor','w')
plot(minPos(1),'Marker','o','MarkerSize',10,'MarkerFaceColor','w','MarkerEdgeColor','k')
hold off
The S-wave anisotropy, in contrast, is a function of the propagation direction as it compares the two S-waves traveling in the same direction
AVs = 200*(vs1-vs2)./(vs1+vs2);
plot(AVs,'complete','upper')
mtexTitle('S-wave anisotropy (%)')
mtexColorbar
A third quantity of interest in seismology is the ratio between P- and S-wave velocity
plot(vp./vs1,'complete','upper')
mtexTitle('Vp/Vs1')
mtexColorbar
Comparison with an Isotropic Medium
It is instructive to compare these velocities with those of an aggregate of randomly oriented Olivine crystals, which we obtain by averaging the stiffness tensor with respect to a uniform ODF. The first output of mean is the Voigt average, see isotropic theory for the Reuss and Hill averages.
C_iso = mean(C,uniformODF(cs))C_iso = stiffnessTensor (y↓→x)
unit : GPa
density: 3.355
rank : 4 (3 x 3 x 3 x 3)
tensor in Voigt matrix representation:
237.56 78.49 78.49 0 0 0
78.49 237.56 78.49 0 0 0
78.49 78.49 237.56 0 0 0
0 0 0 79.54 0 0
0 0 0 0 79.54 0
0 0 0 0 0 79.54The resulting tensor is elastically isotropic. Hence its wave velocities are independent of the propagation direction and are entirely determined by the bulk modulus \(K\), the shear modulus \(G\) and the density
K = C_iso.bulkModulus;
G = C_iso.shearModulus;
vpIso = sqrt((K + 4/3*G)./rho)
vsIso = sqrt(G./rho)vpIso =
8.4147
vsIso =
4.8690which is exactly what the command velocity returns for this tensor
[vp_iso,vs1_iso,vs2_iso] = velocity(C_iso,vector3d.X)vp_iso =
8.4147
vs1_iso =
4.8690
vs2_iso =
4.8690Note that both S-waves now travel with the same speed - there is no shear wave splitting in an isotropic medium. Comparing the isotropic P-wave velocity with the extremes of the single crystal
cprintf([minVp,vpIso,maxVp],'-Lc',{'min Vp' 'isotropic' 'max Vp'})min Vp isotropic max Vp
7.65328 8.41473 9.7735Group Velocity
The velocities computed so far are phase velocities, i.e., they describe how fast a wave front moves along its normal \(\vec n\). Energy, however, travels along the energy velocity vector \(\vec V_e\), which for a lossless medium is a good proxy for the group velocity and is computed by the command energyVector
% an arbitrary, non symmetric propagation direction
x = vector3d.byPolar(45*degree,20*degree);
[vp,vs1,vs2,pp,ps1,ps2] = velocity(C,x);
Ve = energyVector(C,x,vp,pp)Ve = vector3d (y↓→x)
x y z
6.92 1.57 5.11In an anisotropic medium this vector is in general not parallel to the propagation direction - the energy of the wave is deflected sideways. The angle between both directions is
angle(Ve,x) ./ degreeans =
10.7498Its magnitude is at least as large as the phase velocity, while its projection onto the propagation direction reproduces the phase velocity exactly
cprintf([norm(Ve),dot(Ve,x),vp],'-Lc',{'|Ve|' 'Ve.n' 'Vp'})|Ve| Ve.n Vp
8.74413 8.59068 8.59068As for velocity, passing an empty propagation direction together with the spherical velocity and polarization functions returns the energy velocity as a spherical vector field.
Phase Velocity Surfaces
When projected to a plane the different wave speeds
planeNormal = vector3d.X;
% recompute the velocities as spherical functions
[vp,vs1,vs2,pp,ps1,ps2] = velocity(C);
% options for sections
optSec = {'color','interp','linewidth',6,'doNotDraw'};
% options for quiver
optQuiver = {'linewidth',2,'autoScaleFactor',0.35,'doNotDraw'};
optQuiverProp = {'color','k','linewidth',2,'autoScaleFactor',0.25,'doNotDraw'};
prop = S2VectorFieldHarmonic.normal; % the propagation direction
% wave velocities
plotSection(vp,planeNormal,optSec{:},'DisplayName','Vp')
hold on
plotSection(vs1,planeNormal,optSec{:},'DisplayName','Vs1')
plotSection(vs2,planeNormal,optSec{:},'DisplayName','Vs2')
% polarization directions
quiverSection(vp,pp,planeNormal,'color','c',optQuiver{:},'DisplayName','pp')
quiverSection(vs1,ps1,planeNormal,'color','g',optQuiver{:},'DisplayName','ps1')
quiverSection(vs2,ps2,planeNormal,'color','m',optQuiver{:},'DisplayName','ps2')
% plot propagation directions as reference
quiverSection(vp,prop,planeNormal,optQuiverProp{:},'DisplayName','x')
quiverSection(vs1,prop,planeNormal,optQuiverProp{:})
quiverSection(vs2,prop,planeNormal,optQuiverProp{:})
hold off
axis off tight
legend('Vp','Vs1','Vs2','pp','ps1','ps2','x','Location','eastOutSide')
mtexTitle('Phase velocity surface (km/s)')
mtexColorMap blue2red
mtexColorbar('Title','(km/s)','location','southOutSide')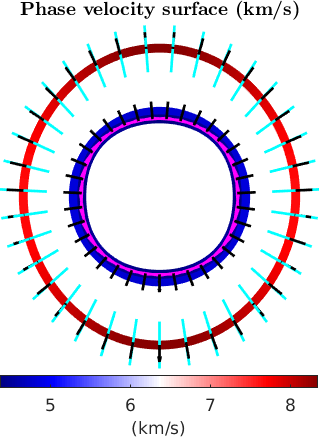
The distance of each curve from the origin is the phase velocity in the corresponding direction, the black arrows mark the propagation direction and the colored arrows the polarization directions.
Slowness Surfaces
Similarly, we can visualize the slowness surfaces (s/km)
% plot slowness surfaces
plotSection(1./vp,planeNormal,optSec{:},'DisplayName','Vp')
hold on
plotSection(1./vs1,planeNormal,optSec{:},'DisplayName','Vs1')
plotSection(1./vs2,planeNormal,optSec{:},'DisplayName','Vs2')
% polarization directions
quiverSection(1./vp,pp,planeNormal,'color','c',optQuiver{:},'DisplayName','pp')
quiverSection(1./vs1,ps1,planeNormal,'color','g',optQuiver{:},'DisplayName','ps1')
quiverSection(1./vs2,ps2,planeNormal,'color','m',optQuiver{:},'DisplayName','ps2')
% plot propagation directions as reference
quiverSection(1./vp,prop,planeNormal,optQuiverProp{:},'DisplayName','x')
quiverSection(1./vs1,prop,planeNormal,optQuiverProp{:})
quiverSection(1./vs2,prop,planeNormal,optQuiverProp{:})
hold off
axis off tight
legend('Vp','Vs1','Vs2','pp','ps1','ps2','x','Location','eastOutSide')
mtexTitle('Slowness surface (s/km)')
mtexColorMap blue2red
mtexColorbar('Title','(s/km)','location','southOutSide')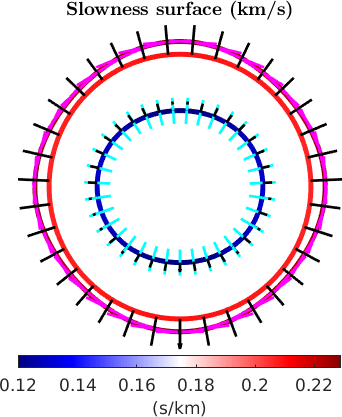
An Overview Plot
All the above quantities are summarized in a single figure by the command plotSeismicVelocities
plotSeismicVelocities(C)
How to apply this to a polycrystalline aggregate with a crystallographic preferred orientation is explained in the section seismic properties of aggregates.
set back default colormap
setMTEXpref('defaultColorMap',WhiteJetColorMap)