Euler Angle Sections

Euler Angle Sections edit page

TODO: Please help extending this section

cs = crystalSymmetry.load('Al-Aluminum.cif')

ori1 = orientation.brass(cs);
ori2 = orientation.copper(cs);
f = fibre.beta(cs);

odf = 0.2*unimodalODF(ori1) + ...
      0.3*unimodalODF(ori2) + ...
      0.5*fibreODF(f)

cs = crystalSymmetry
 
  mineral : Aluminum
  symmetry: m-3m    
  elements: 48      
  a, b, c : 4, 4, 4 
 
 
odf = SO3FunComposition (Aluminum → y↑→x)
 
  multimodal components
  kernel: de la Vallee Poussin, halfwidth 10°
  center: 2 orientations
 
  Bunge Euler angles in degree
  phi1     Phi    phi2  weight
    35      45       0     0.2
    90 35.2644      45     0.3
 
  fibre component
  kernel: de la Vallee Poussin, halfwidth 10°
  fibre : (12 6 11) || -1,-1,4
  weight: 0.5

Plotting an ODF in two dimensional sections through the orientation space is done using the command plot. By default the sections are at constant angles of $\varphi_2$ . The number of sections can be specified by the option 'sections'

plot(odf,'sections',9,'silent','layout',[5 2])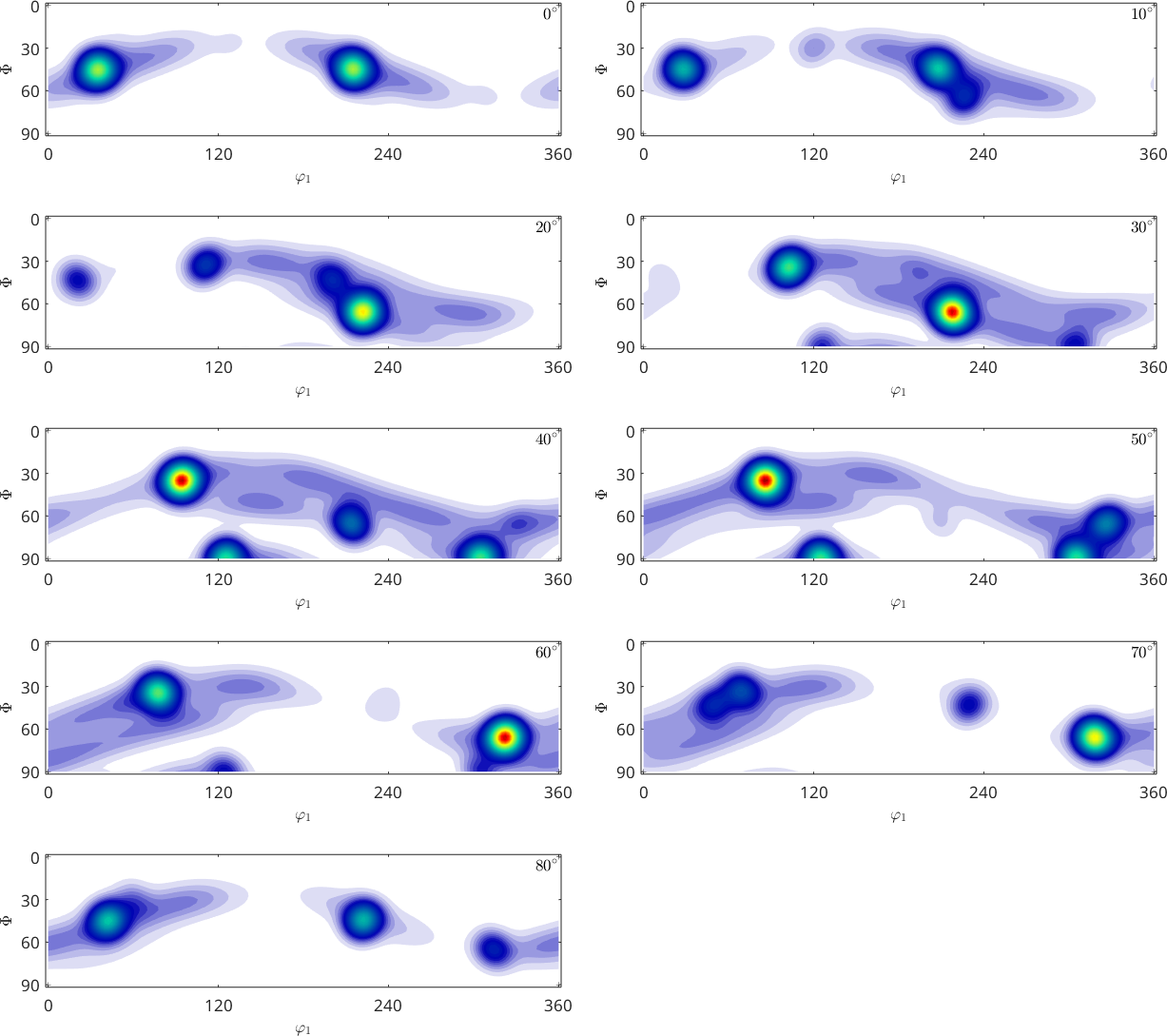

annotate(ori1,'MarkerSize',15)
annotate(ori2,'Marker','v','MarkerSize',15)

plot(f,'linewidth',2,'add2all')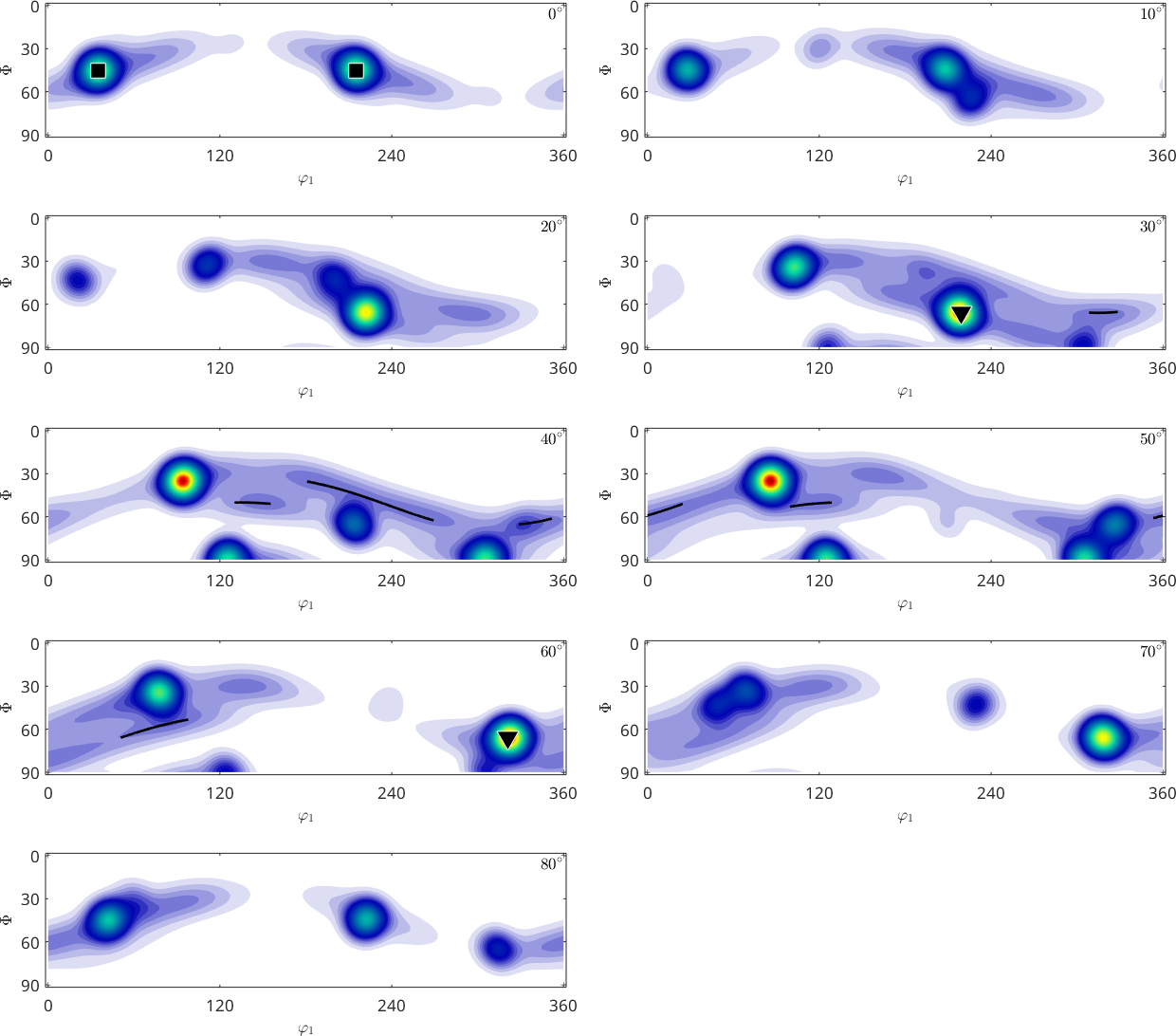

One can also specify the $\varphi_2$ angles of the sections explicitly

plot(odf,'phi2',[25 30 35 40]*degree,'silent')

annotate(ori1,'MarkerSize',15)
annotate(ori2,'Marker','v','MarkerSize',15)

plot(f,'linewidth',2,'add2all')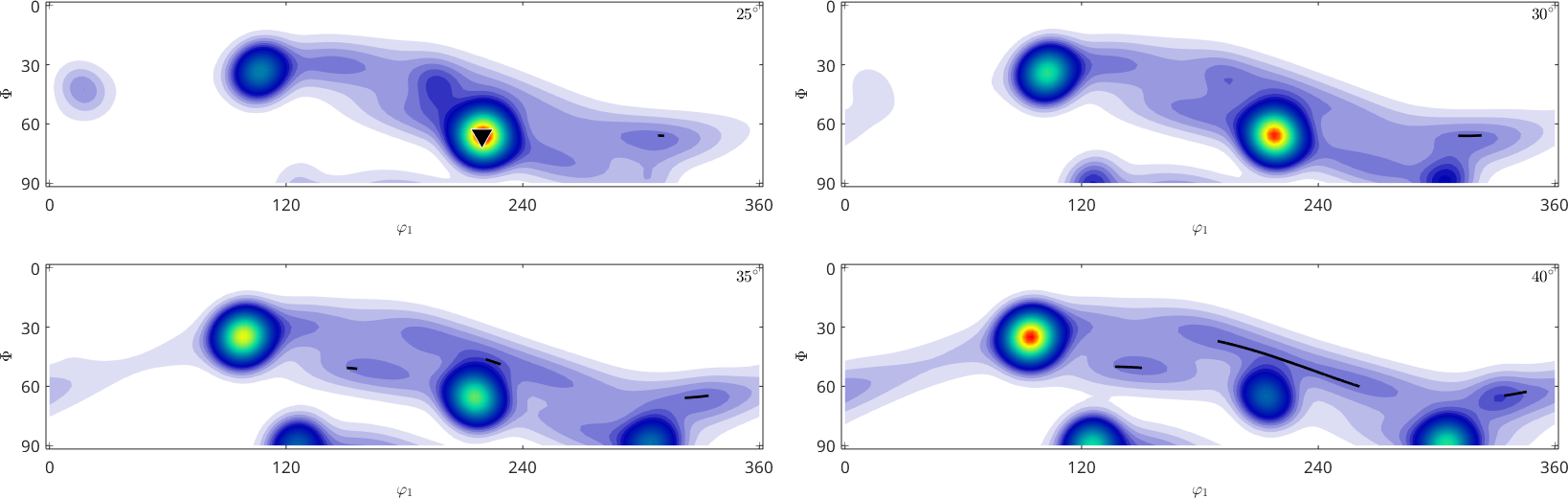

Beside the standard phi2 sections MTEX supports also sections according to all other Euler angles.

phi2 (default)
phi1
gamma (Matthies Euler angles)
sigma (alpha+gamma)

plotSection(odf)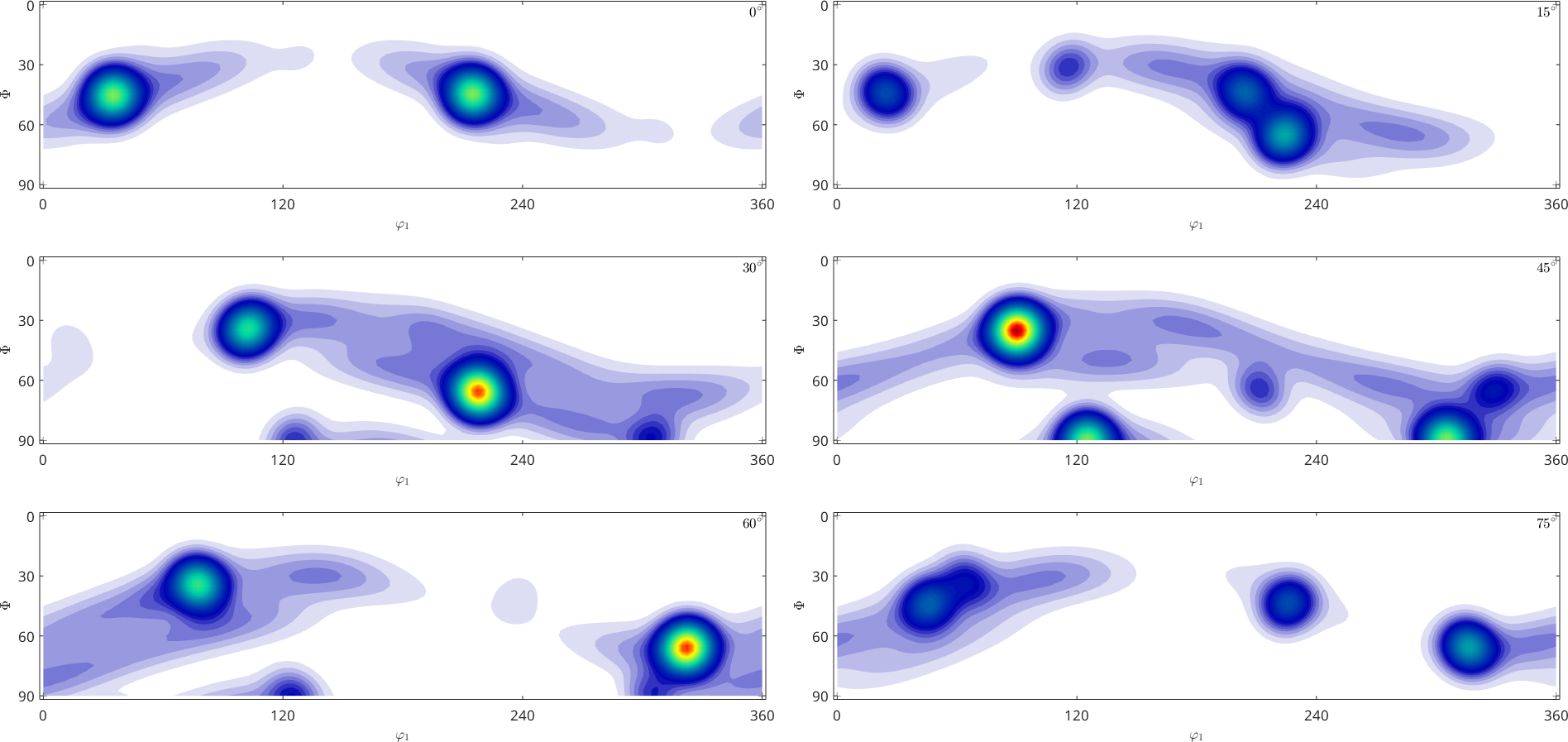

By default this command represents the ODF in the Bunge Euler angle space $\varphi_1$ , $\Phi$ , $\varphi_2$ . The range of the Euler angles depends on the crystal symmetry according to the following table

symmetry	1	2	222	3	32	4	422	6	622	23	432
$\varphi_1$	$360^{\circ}$	$360^{\circ}$	$360^{\circ}$	$360^{\circ}$	$360^{\circ}$	$360^{\circ}$	$360^{\circ}$	$360^{\circ}$	$360^{\circ}$	$360^{\circ}$	$360^{\circ}$
$\Phi$	$180^{\circ}$	$180^{\circ}$	$90^{\circ}$	$180^{\circ}$	$90^{\circ}$	$180^{\circ}$	$90^{\circ}$	$180^{\circ}$	$90^{\circ}$	$90^{\circ}$	$90^{\circ}$
$\varphi_2$	$360^{\circ}$	$180^{\circ}$	$180^{\circ}$	$120^{\circ}$	$120^{\circ}$	$90^{\circ}$	$90^{\circ}$	$60^{\circ}$	$60^{\circ}$	$180^{\circ}$	$90^{\circ}$

Note that for the last two symmetries the three fold axis is not taken into account, i.e., each orientation appears three times within the Euler angle region. The first Euler angle is not restricted by any crystal symmetry, but only by specimen symmetry. For an arbitrary symmetry the bounds of the fundamental region can be computed by the command fundamentalRegionEuler

Specimen Symmetry

As we can see from the above table the first Euler angle $\varphi_1$ ranges for all symmetries from zero to 360 degree. The only way to restrict this angle is to consider specimen symmetry. In the classical case of orthotropic specimen symmetry the range of the first Euler angle reduces to 90 degree and we obtain the common square shaped ODF section plots

odf.SS = specimenSymmetry('222');

plot(odf,'sections',18,'layout',[5 4],...
  'coordinates','off','xlabel','','ylabel','')