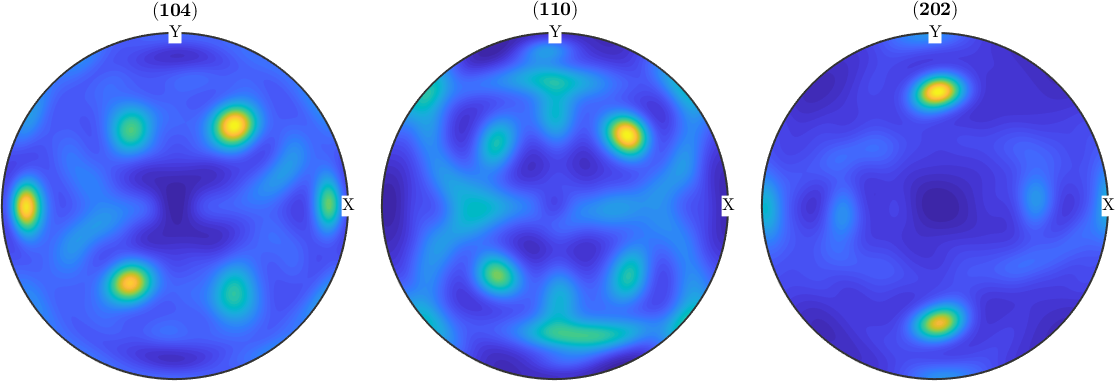
This section describes various possibilities to visualize pole figure data. Lets start by loading some XRD data
mtexdata ptxpf = PoleFigure (y↑→x)
crystal symmetry : mmm
h = (104), r = 72 x 17 points
h = (110), r = 72 x 17 points
h = (202), r = 72 x 17 pointsBy default MTEX plots pole figures by drawing a circle at every measurement position of a pole figure and coloring it corresponding to the measured intensity.
plot(pf)
mtexColorbar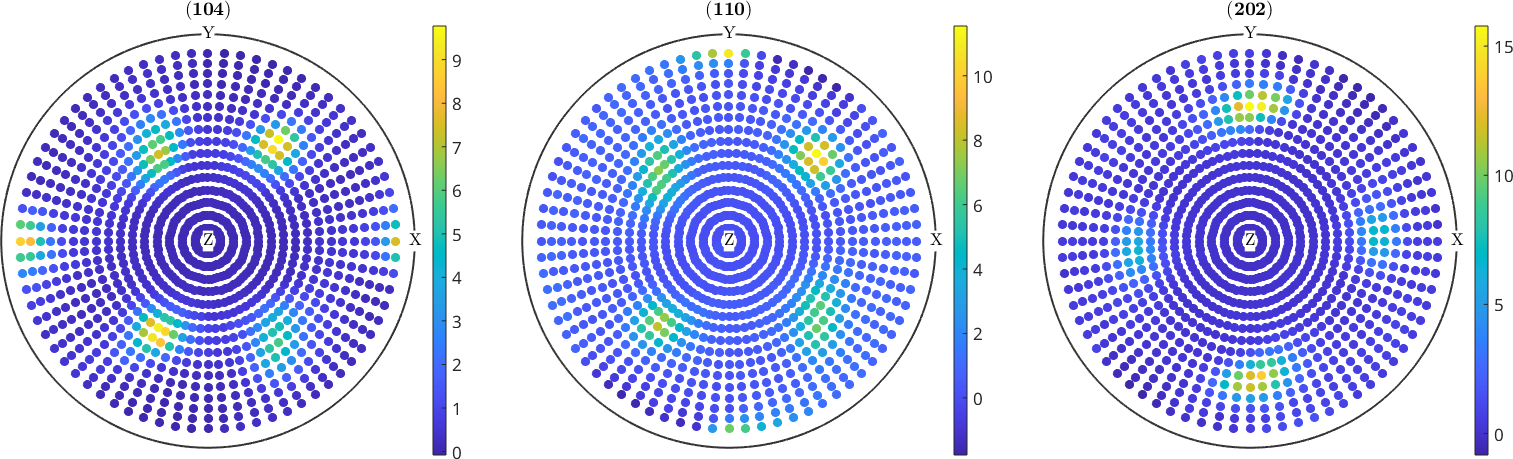
MTEX tries to guess the right size of the circle in order to produce a pleasing result. However, you can adjust this size using the option MarkerSize.
plot(pf,'MarkerSize',4)
mtexColorbar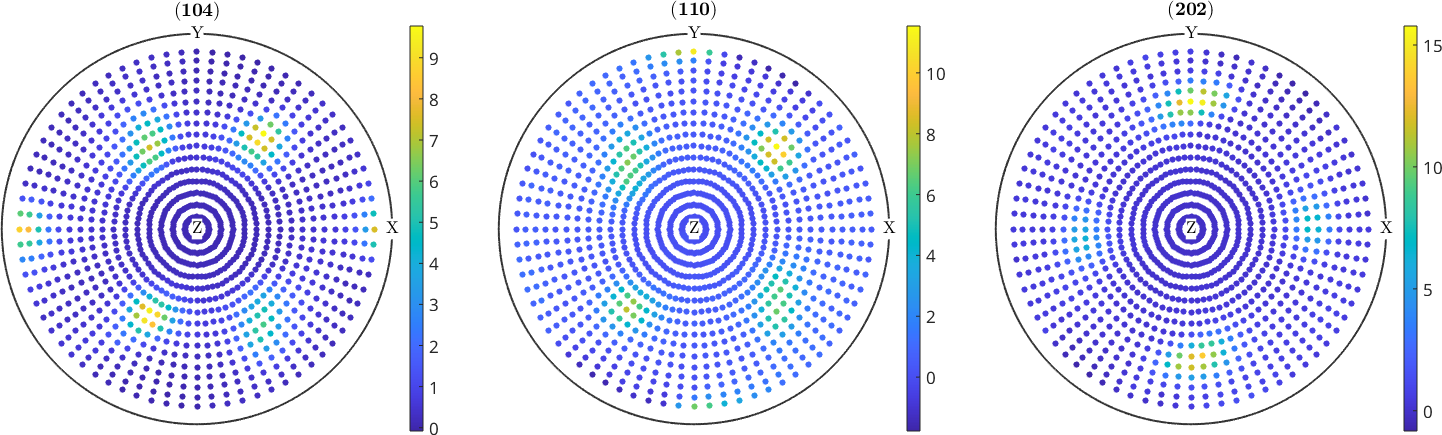
Contour Plots
Some people like to have their raw pole figures to be drawn as contour plots. This feature is not yet generally supported by MTEX. Note that measured pole figure may be given at a very irregular grid which would make it necessary to interpolate before drawing contours. In this case, however, it seems to be more reasonable to first compute an ODF and than to draw contour plots of the recalculated pole figures.
Nevertheless, MTEX offers basic contour plots in the case of regular measurement grids.
plot(pf,'contourf')
mtexColorbar
mtexColorMap parula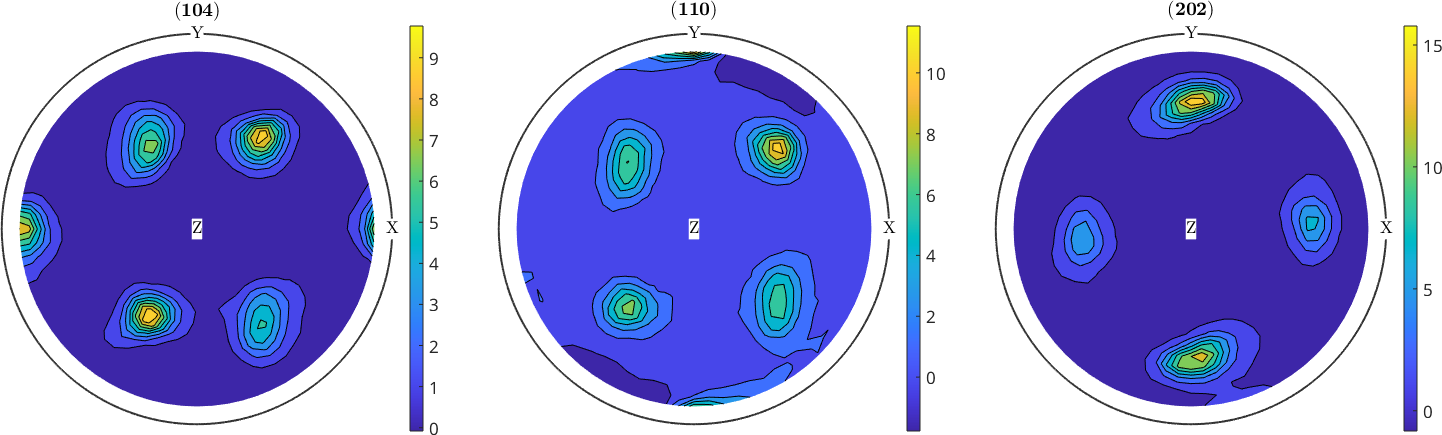
When drawing a colorbar next to the pole figure plots it is necessary to have the same color coding in all plots. This can be done as following
mtexColorbar % remove colorbars
setColorRange('equal');
mtexColorbar % add a single colorbar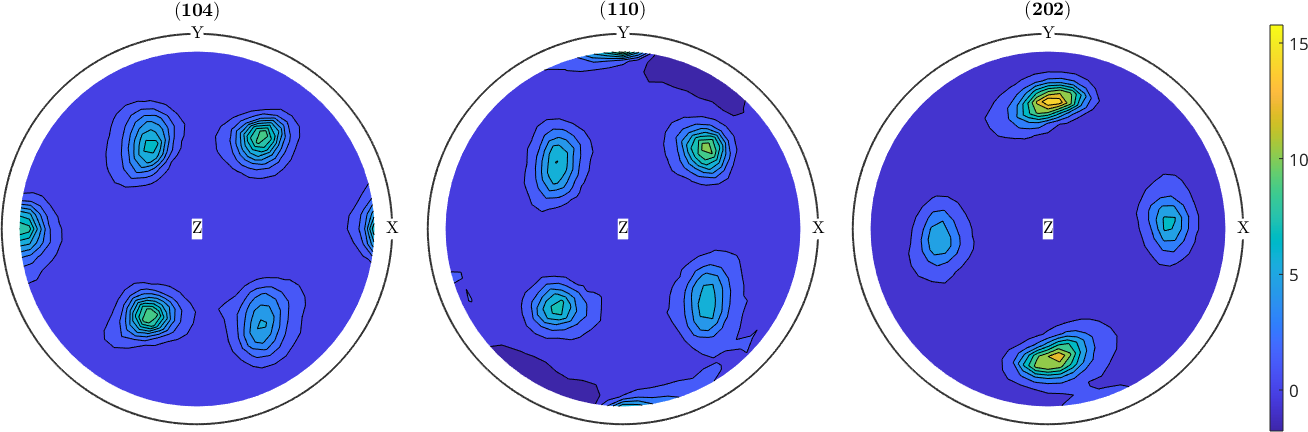
Plotting Recalculated Pole Figures
In order to draw recalculated one first needs to compute an ODF.
odf = calcODF(pf,'silent')odf = SO3FunRBF (mmm → y↑→x)
multimodal components
kernel: de la Vallee Poussin, halfwidth 5°
center: 29772 orientations, resolution: 5°
weight: 1Now smooth pole figures can be plotted for arbitrary crystallographic directions.
plotPDF(odf,pf.h,'antipodal')
mtexColorMap parula