This example demonstrates the most important MTEX tools for analysing Pole Figure Data.
% specify crystal and specimen symmetry
CS = crystalSymmetry('-3m',[4.9 4.9 5.4]);
% specify file names
fname = {...
fullfile(mtexDataPath,'PoleFigure','dubna','Q(10-10)_amp.cnv'),...
fullfile(mtexDataPath,'PoleFigure','dubna','Q(10-11)(01-11)_amp.cnv'),...
fullfile(mtexDataPath,'PoleFigure','dubna','Q(11-22)_amp.cnv')};
% specify crystal directions
h = {Miller(1,0,-1,0,CS),...
[Miller(0,1,-1,1,CS),Miller(1,0,-1,1,CS)],... % superposed pole figures
Miller(1,1,-2,2,CS)};
% specify structure coefficients
c = {1,[0.52 ,1.23],1};
% import data
pf = PoleFigure.load(fname,h,CS,'interface','dubna','superposition',c);
plot(pf)
mtexColorbar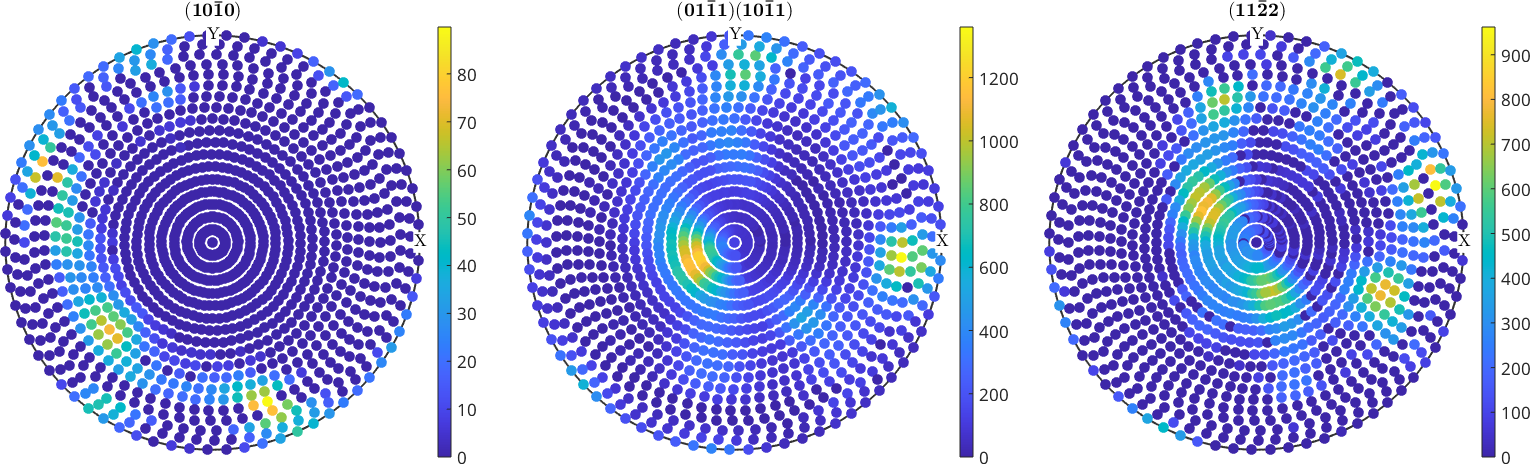
Extract information from imported pole figure data
Get raw data
Data stored in a PoleFigure variable can be extracted by
I = pf.intensities; % intensities
h = pf.h; % Miller indice
r = pf.r; % specimen directionsBasic Statistics
There are also some basic statics on pole figure intensities
min(pf)
max(pf)
isOutlier(pf);ans =
0 0 0
ans =
1.0e+03 *
0.0898 1.3600 0.9620Manipulate pole figure data
pf_modified = pf(pf.r.theta < 70*degree | pf.r.theta > 75*degree)
plot(pf_modified)pf_modified = PoleFigure (y↑→x)
crystal symmetry : -3m1, X||a*, Y||b, Z||c*
h = (10-10), r = 1 x 1224 points
h = (01-11)(10-11), r = 1 x 1224 points
h = (11-22), r = 1 x 1224 points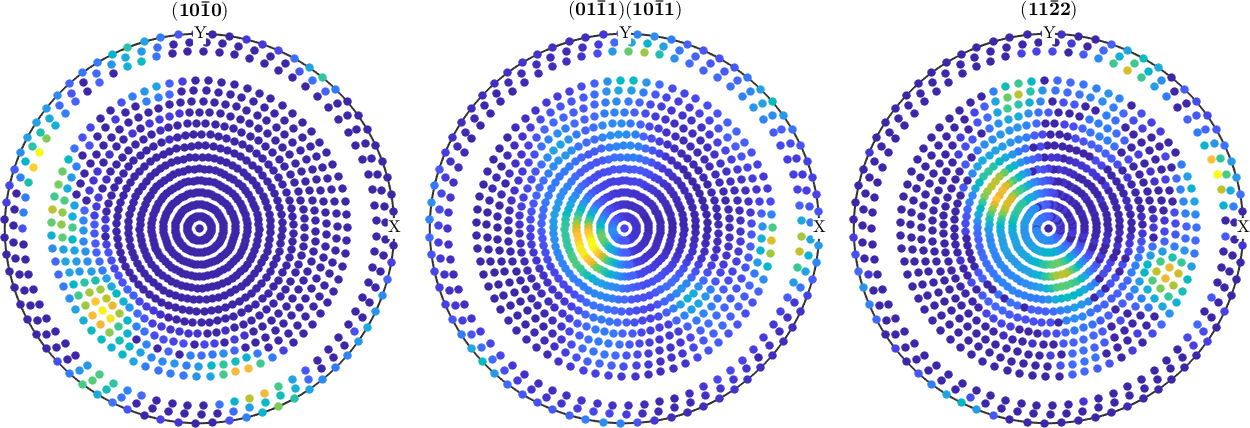
rot = rotation.byAxisAngle(xvector-yvector,25*degree);
pf_modified = rotate(pf,rot)
plot(pf_modified)pf_modified = PoleFigure (y↑→x)
crystal symmetry : -3m1, X||a*, Y||b, Z||c*
h = (10-10), r = 72 x 19 points
h = (01-11)(10-11), r = 72 x 19 points
h = (11-22), r = 72 x 19 points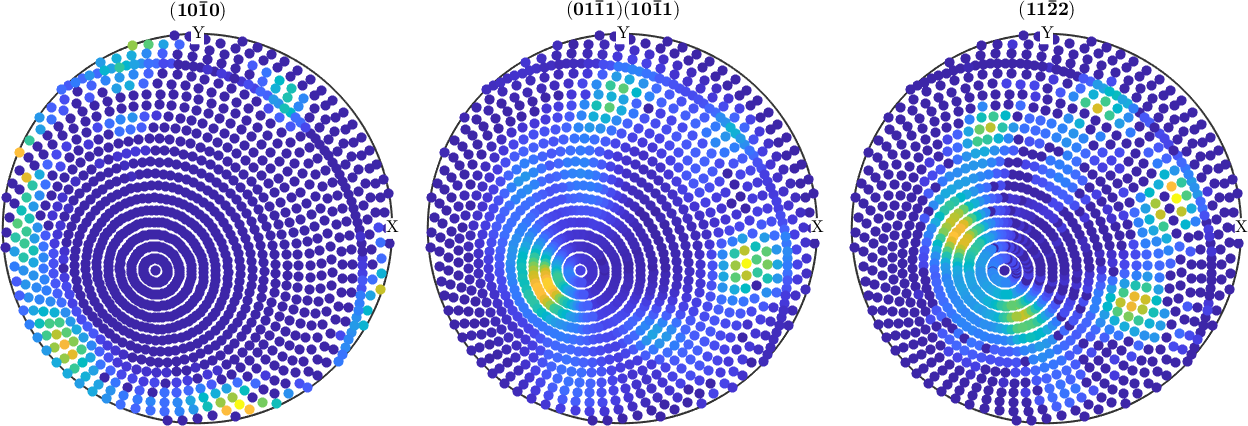
PDF - to - ODF Reconstruction
rec = calcODF(pf,'RESOLUTION',10*degree,'iter_max',6)
plotPDF(rec,h)
mtexColorbarrec = SO3FunRBF (-3m1 → y↑→x)
multimodal components
kernel: de la Vallee Poussin, halfwidth 10°
center: 2472 orientations, resolution: 10°
weight: 1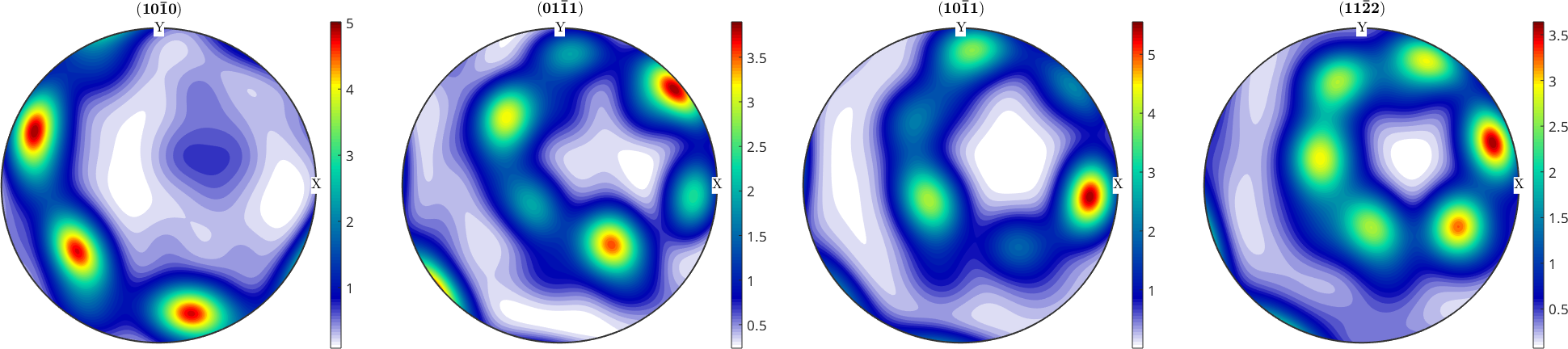
odf = SantaFe
% define specimen directions
r = regularS2Grid('antipodal')odf = SO3FunRBF (m-3m → y↑→x (222))
uniform component
weight: 0.73
unimodal component
kernel: van Mises Fisher, halfwidth 10°
center: 1 orientations
Bunge Euler angles in degree
phi1 Phi phi2 weight
296.565 48.1897 26.5651 0.27
r = S2Grid
size: 72 x 19
antipodal: truedefine crystal directions
h = [Miller(1,0,0,odf.CS),Miller(1,1,0,odf.CS),Miller(1,1,1,odf.CS)];simulate pole figure data
pf_SantaFe = calcPoleFigure(SantaFe,h,r);estimate an ODF with ghost correction
rec = calcODF(pf_SantaFe,'RESOLUTION',10*degree,'background',10)
plot(rec,'sections',6)rec = SO3FunRBF (m-3m → y↑→x (222))
uniform component
weight: 0.74
multimodal components
kernel: de la Vallee Poussin, halfwidth 10°
center: 150 orientations, resolution: 10°
weight: 0.26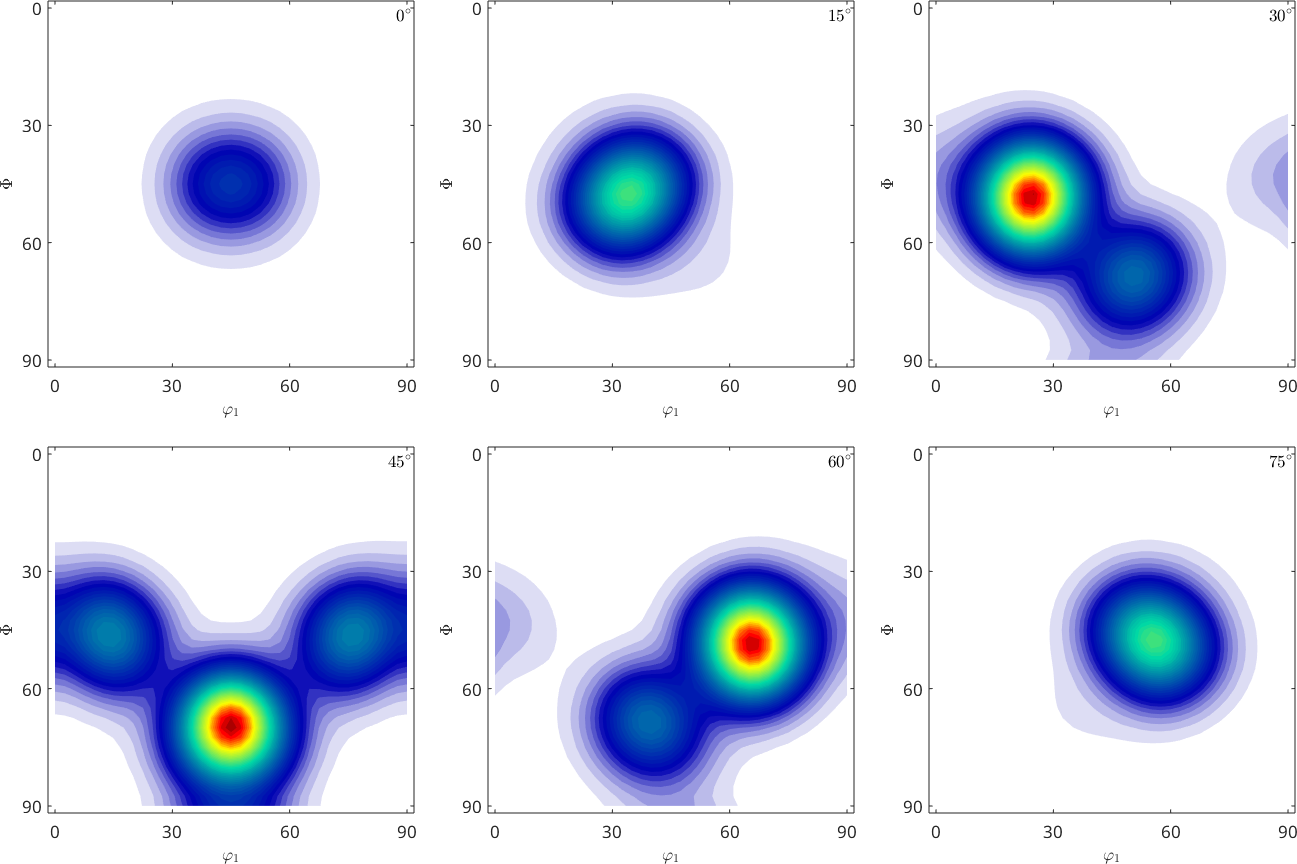
without ghost correction
rec_ng = calcODF(pf_SantaFe,'RESOLUTION',10*degree,'background',10,'NoGhostCorrection')
plot(rec_ng,'sections',6)rec_ng = SO3FunRBF (m-3m → y↑→x (222))
multimodal components
kernel: de la Vallee Poussin, halfwidth 10°
center: 150 orientations, resolution: 10°
weight: 1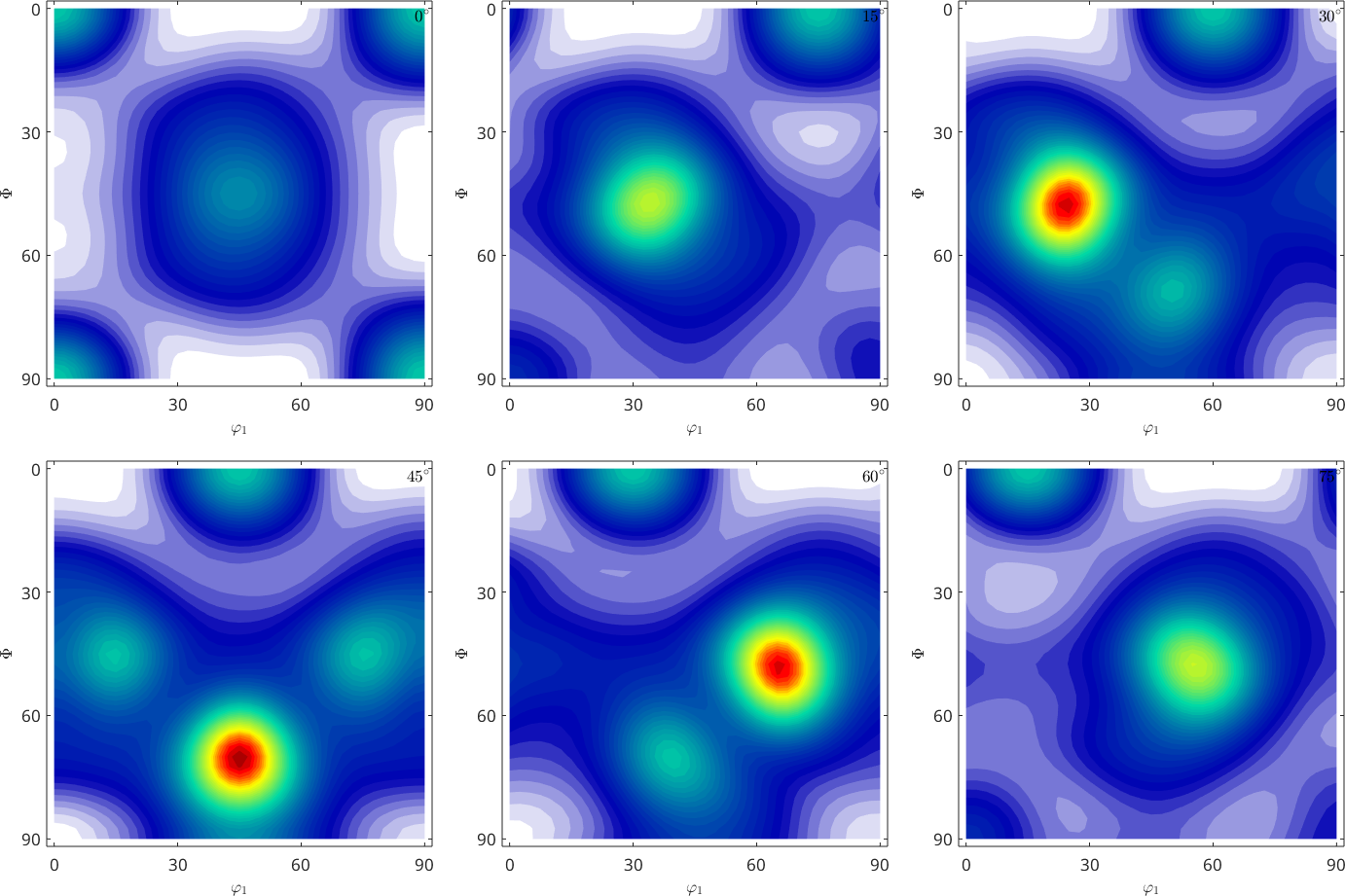
Error Analysis
calcError(pf_SantaFe,rec)
calcError(pf_SantaFe,rec_ng)ans =
0.0245 0.0286 0.0270
ans =
0.0358 0.0283 0.0252Difference plot
plotDiff(pf_SantaFe,rec)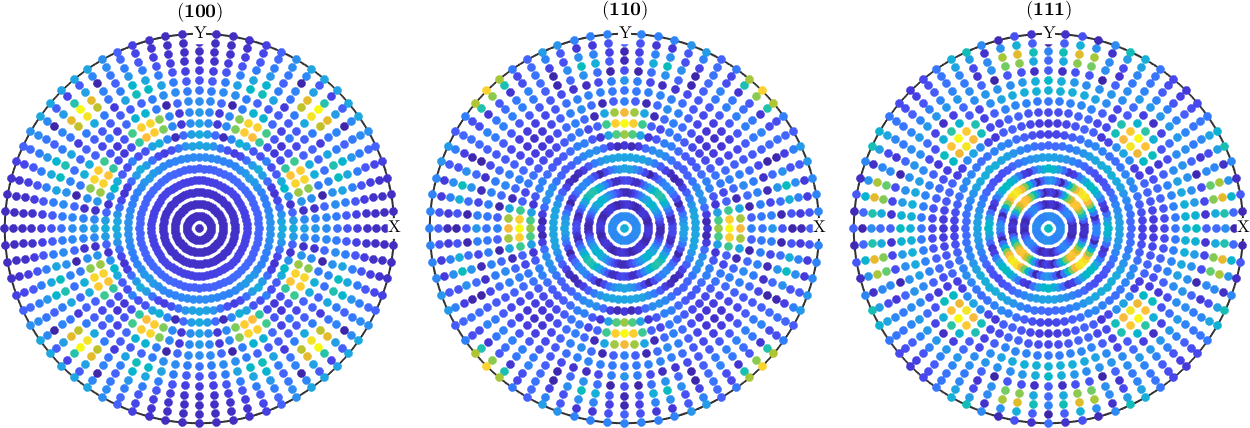
ODF error
calcError(SantaFe,rec)
calcError(SantaFe,rec_ng)ans =
0.0359
ans =
0.0893Exercises
3)
a) Load the pole figure data of a quartz specimen from: data/dubna!
b) Inspect the raw data. Are there noticeable problems?
c) Compute an ODF from the pole figure data.
d) Plot some pole figures of that ODF and compare them to the measured pole figures.
e) Compute the RP errors for each pole figure.
f) Plot the difference between the raw data and the calculated pole figures. What do you observe?
g) Remove the erroneous values from the pole figure data and repeat the ODF calculation. How do the RP error change?
h) Vary the number of pole figures used for the ODF calculation. What is the minimum set of pole figures needed to obtain a meaningful ODF?