Grain Boundary Normal Distribution

Grain Boundary Normal Distribution edit page

In this section we discuss a stereographic approach of determining the grain boundary normal distribution from two dimensional EBSD data following the publications

D.M. Saylor, G.S. Rohrer: Determining crystal habits from observations of planar sections in J. Am. Ceram. Soc., 85(11):2799–2804, 2002.

R. Hielscher, R. Kilian, K. Marquardt, E. Wünsche: Efficient computation of the grain boundary normal distribution from two dimensional EBSD data, not yet published.

We start our demonstration by importing some EBSD data and reconstructing the grain structure.

mtexdata csl

[grains,ebsd.grainId] = calcGrains(ebsd);

grains = smooth(grains,10)

plot(ebsd,ebsd.orientations)
hold on
plot(grains.boundary,'lineWidth',2)
hold off

ebsd = EBSD
 
 Phase   Orientations  Mineral         Color  Symmetry  Crystal reference frame
    -1  154107 (100%)     iron  LightSkyBlue      m-3m                         
 
 Properties: ci, error, iq
 Scan unit : um
 X x Y x Z : [0 511] x [0 300] x [0 0]
 Normal vector: (0,0,1)
 
 
grains = grain2d
 
 Phase  Grains  Pixels  Mineral  Symmetry  Crystal reference frame
    -1     885  154107     iron      m-3m                         
 
 boundary segments: 23579 (17770 µm)
 inner boundary segments: 93 (67 µm)
 triple points: 1451
 
 Properties: meanRotation, GOS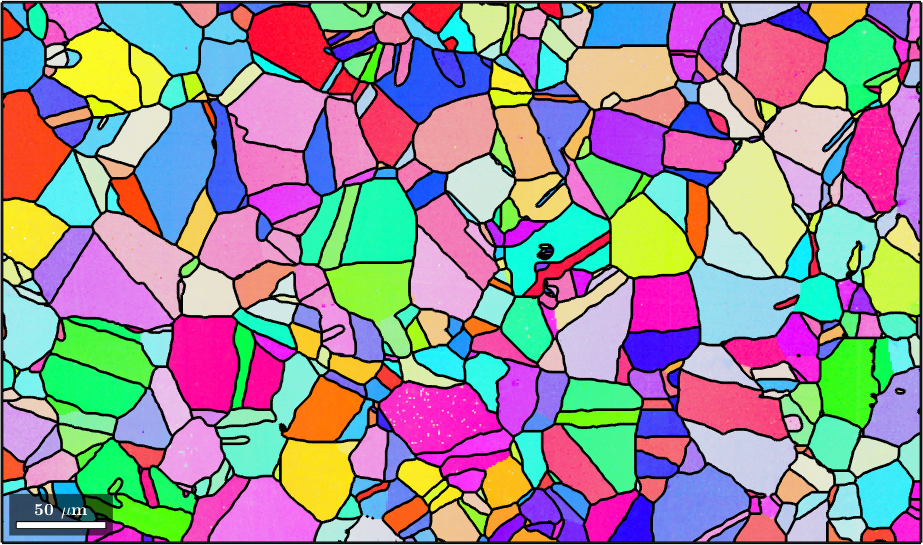

Misorientation angle at grain boundaries

Next we separate the grain boundaries according to the misorientation angle. More precisely, we distinguish those grain boundaries with misorientation angle larger then 57 degree and those with a smaller misorientation angle.

gB = grains.boundary('indexed');
cond = gB.misorientation.angle > 57 * degree;

plot(ebsd,ebsd.orientations)
hold on
plot(grains.boundary,'lineWidth',2)
plot(gB(cond),'lineWidth',2,'lineColor','w')
hold off

Using the command calcGBPD we can now compute the grain boundary plane distribution from a list of two dimensional traces.

gbnd1 = calcGBPD(gB(cond),ebsd)
gbnd2 = calcGBPD(gB(~cond),ebsd)

contourf(gbnd1,'colorrange',[0.8 1.5])
mtexTitle('GBPD for misorientation angle \(> 57^{\circ}\)')
mtexColorMap parula
nextAxis
contourf(gbnd2,'colorrange',[0.8 1.5])
mtexTitle('GBPD for misorientation angle \(< 57^{\circ}\)')
mtexColorMap parula
mtexColorbar

gbnd1 = S2FunHarmonicSym (iron)
  bandwidth: 48
  antipodal: true
  isReal: true
 
 
gbnd2 = S2FunHarmonicSym (iron)
  bandwidth: 48
  antipodal: true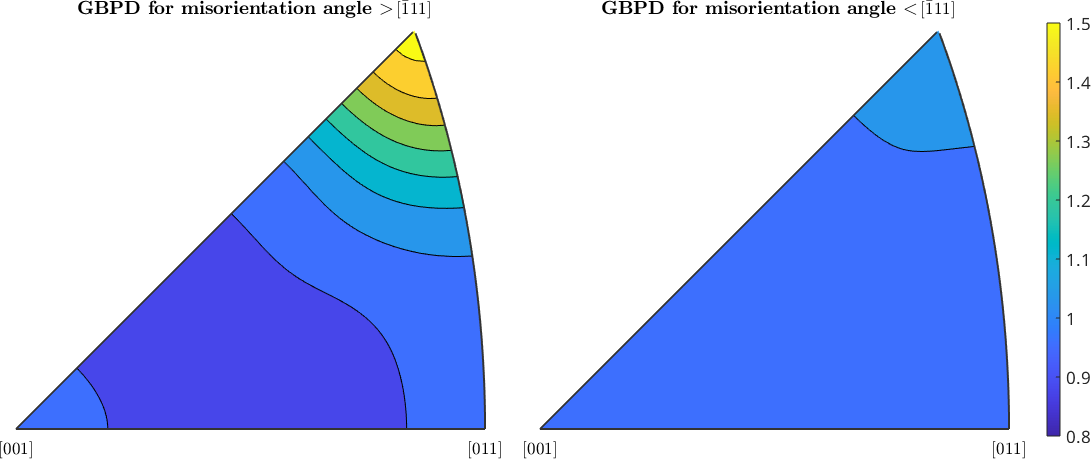
  isReal: true

We observe that for a twinning grain boundaries the boundary plane is mostly parallel to the (111) plane, while for all other grain boundaries no preferred boundary plane exists.