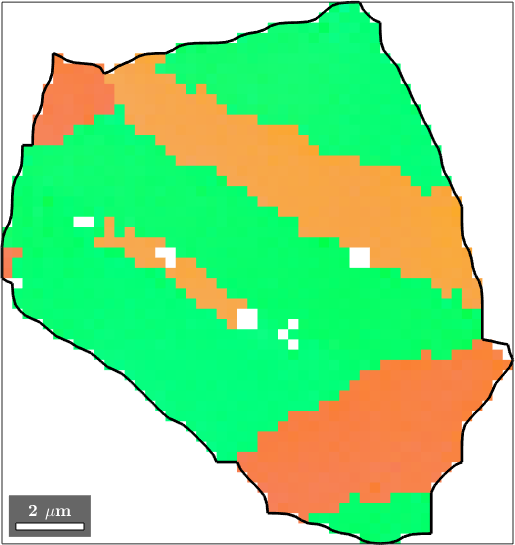
Merging grains may be useful when reconstructing parent grain structures, i.e., before phase transition or before twinning. In this section we will use a twinning example for illustration. Lets start by importing some Magnesium data and reconstructing the grain structure:
% load some example data
mtexdata twins silent
% segment grains
[grains,ebsd.grainId,ebsd.mis2mean] = calcGrains(ebsd('indexed'),'angle',5*degree,'minPixel',3);
% smooth them
grains = grains.smooth(5);
% visualize the grains
plot(grains,grains.meanOrientation)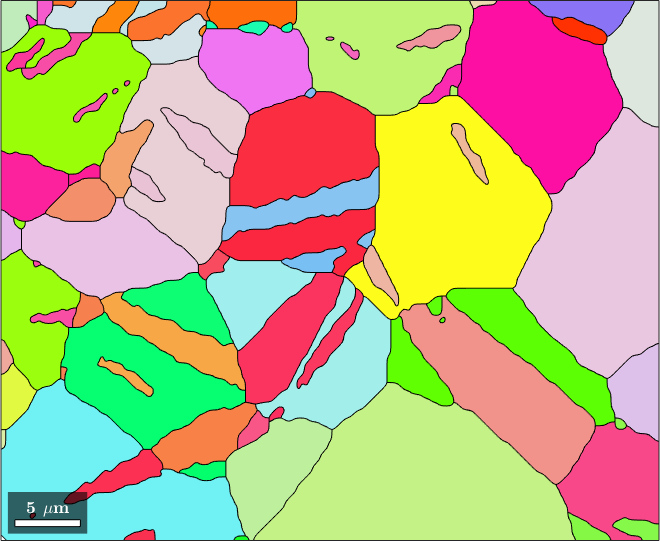
Next we identify all twinning boundaries
% define twinning misorientation
CS = grains.CS;
twinning = orientation.map(Miller(0,1,-1,-2,CS),Miller(0,-1,1,-2,CS),...
Miller(2,-1,-1,0,CS),Miller(2,-1,-1,0,CS));
% extract all Magnesium Magnesium grain boundaries
gB = grains.boundary('Magnesium','Magnesium');
% and check which of them are twinning boundaries with threshold 5 degree
isTwinning = angle(gB.misorientation,twinning) < 5*degree;
twinBoundary = gB(isTwinning)
% plot the twinning boundaries
hold on
plot(twinBoundary,'linecolor','w','linewidth',4,'displayName','twin boundary')
hold offtwinBoundary = grainBoundary
Segments length mineral 1 mineral 2
1649 361 µm Magnesium Magnesium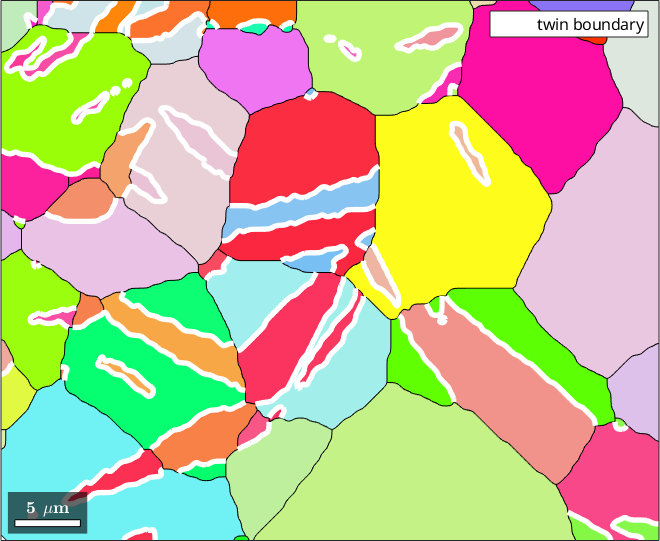
Merge grains along boundaries
The command merge will merge grains together that have a common boundary which is specified as the second argument. In our example we want to merge all grains that have a common twinning boundary so we do
[mergedGrains,parentId] = merge(grains,twinBoundary);
% plot the merged grains
hold on
plot(mergedGrains.boundary,'linecolor','k','linewidth',2.5,'linestyle','-',...
'displayName','merged grains')
hold off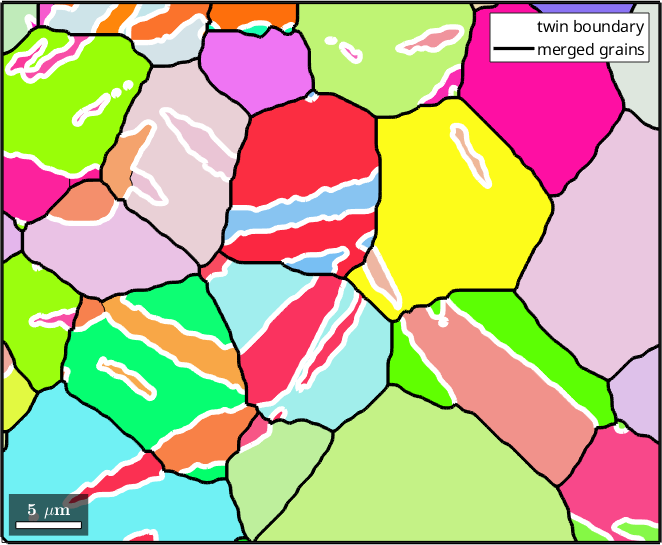
Grain relationships
The second output argument paraentId of merge is a list with the same size as the child grains which indicates for each child grain into which parent grain it has been merged. The id of the common grain is usually different from the ids of the merged grains and can be found by
mergedGrains(16).idans =
16Hence, we can find all childs of grain 16 by
childs = grains(parentId == mergedGrains(16).id)childs = grain2d (y↑→x)
Phase Grains Pixels Mineral Symmetry Crystal reference frame
1 8 1698 Magnesium 6/mmm X||a*, Y||b, Z||c*
boundary segments: 442 (103 µm)
inner boundary segments: 0 (0 µm)
triple points: 25
Id Phase Pixels meanRotation GOS
6 1 40 (178°,90°,236°) 0.0076
14 1 254 (81°,25°,187°) 0.011
17 1 4 (80°,26°,189°) 0.014
19 1 38 (95°,145°,186°) 0.006
24 1 774 (178°,90°,235°) 0.01
28 1 45 (80°,25°,188°) 0.011
29 1 293 (94°,145°,185°) 0.0091
33 1 250 (179°,89°,235°) 0.011Estimate twin area fraction
Determining which of the measured grains are original grains and which are twins is a tough problem. Here we make a very simple assumption by labeling those areas as twins that make up less than half of the merged (original) parent grain
% extract grain area for faster access
gArea = grains.area;
% loop over mergedGrains and determine children that are not twins
isTwin = true(grains.length,1);
for i = 1:mergedGrains.length
% get child ids
childId = find(parentId==i);
% cluster grains of similar orientations
[fId,center] = calcCluster(grains.meanOrientation(childId),'maxAngle',...
15*degree,'method','hierarchical','silent');
% compute area of each cluster
clusterArea = accumarray(fId,gArea(childId));
% label the grains of largest cluster as original grain
[~,fParent] = max(clusterArea);
isTwin(childId(fId==fParent)) = false;
end
% compute the area fraction of twins
sum(area(grains(isTwin)))/sum(area(grains)) * 100
% visualize the result
close all
plot(grains(~isTwin),'FaceColor','darkgray','displayName','not twin')
hold on
plot(grains(isTwin),'FaceColor','red','displayName','twin')
hold on
plot(mergedGrains.boundary,'linecolor','k','linewidth',2,'linestyle','-',...
'displayName','merged grains')
mtexTitle('twin id')ans =
16.6282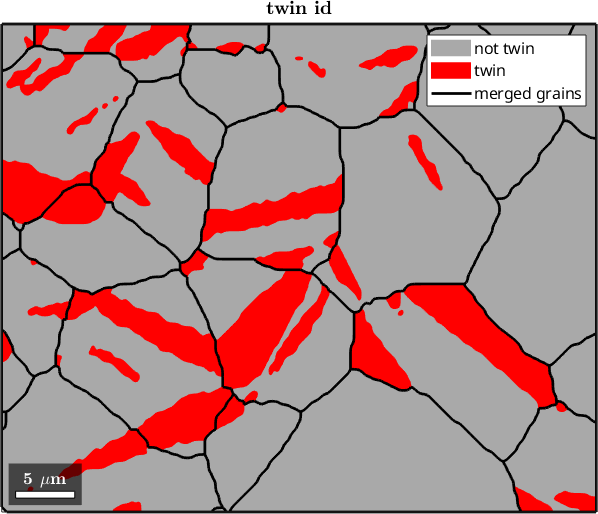
The parentId may also be used to compute properties of the parent grains by averaging over the corresponding child grain properties. This can be done with the MATLAB command accumarray
% this averages the GOS of the child grains into the parent grains
mergedGrains.prop.GOS = accumarray(parentId,grains.GOS,size(mergedGrains),@mean);
% visualize the result
close all
plot(grains,grains.GOS ./ degree)
hold on
plot(mergedGrains.boundary,'lineColor','white','lineWidth',2)
mtexTitle('original GOS')
nextAxis(1,2)
plot(mergedGrains,mergedGrains.GOS ./ degree)
mtexTitle('merged GOS')
mtexColorbar
setColorRange([0,1.5])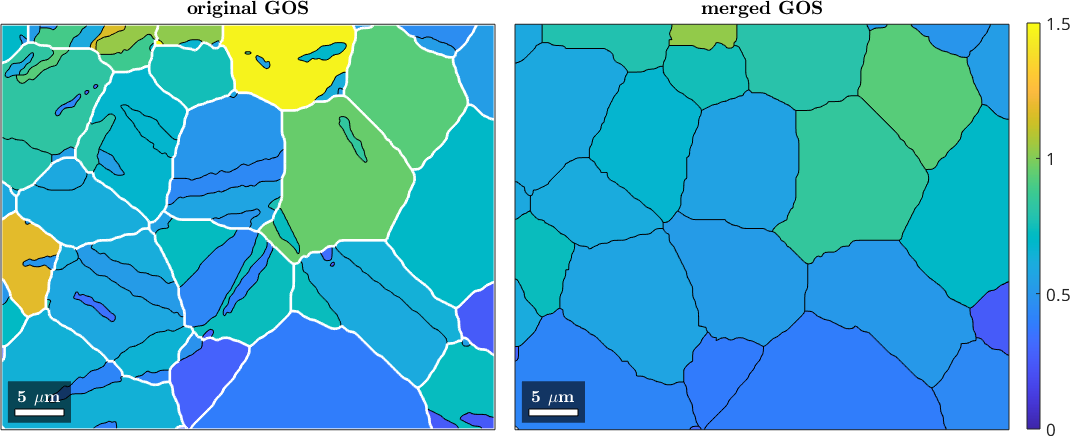
The above result is a bit unrealistic since the averages are computed between the childs ignoring their relative areas. A better approach is to compute a weighted average by the following lines.
% extract GOS and area
childGOS = grains.GOS;
childArea = grains.area;
% compute the weighted averages
mergedGrains.prop.GOS = accumarray(parentId,1:length(grains),size(mergedGrains),...
@(id) nanmeanWeights(childGOS(id),childArea(id)));
nextAxis(1,3), hold on
plot(mergedGrains,mergedGrains.GOS ./ degree)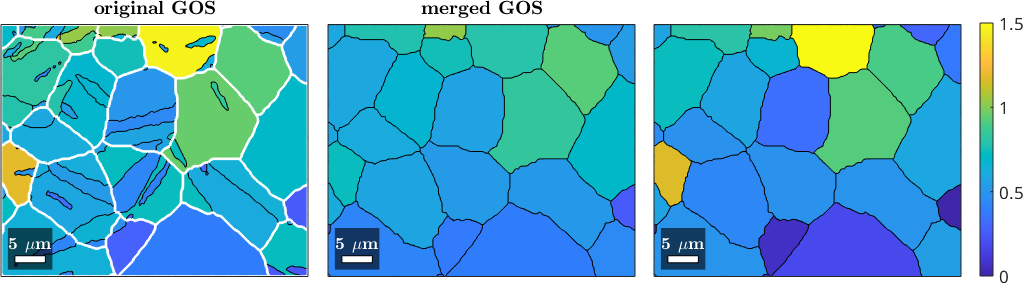
Setting Up the EBSD Data for the Merged Grains
Note that the Id's of the merged grains does not fit the grainIds stored in the initial ebsd variable. As a consequence, the following command will not give the right result
close all
plot(mergedGrains(16).boundary,'linewidth',2)
hold on
plot(ebsd(mergedGrains(16)),ebsd(mergedGrains(16)).orientations)
hold off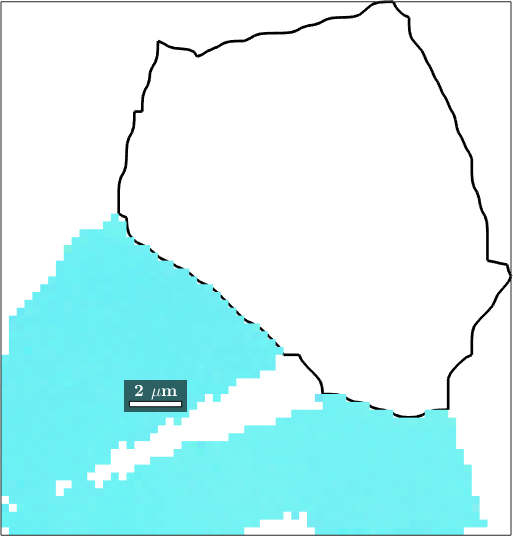
In order to update the grainId in the ebsd variable to the merged grains, we proceed as follows.
% copy ebsd data into a new variable to not change the old data
ebsd_merged = ebsd;
% update the grainIds to the parentIds
ebsd_merged('indexed').grainId = parentId(grains.id2ind(ebsd('indexed').grainId))ebsd_merged = EBSD (y↑→x)
Phase Orientations Mineral Color Symmetry Crystal reference frame
0 85 (0.37%) notIndexed
1 22794 (100%) Magnesium LightSkyBlue 6/mmm X||a*, Y||b, Z||c*
Properties: bands, bc, bs, error, mad, grainId, mis2mean
Scan unit : um
X x Y x Z : [0, 50] x [0, 41] x [0, 0]
Normal vector: (0,0,1)Now the variable ebsd_merged can be indexed by the merged grains, i.e.
plot(ebsd_merged(mergedGrains(16)),ebsd_merged(mergedGrains(16)).orientations)
hold on
plot(mergedGrains(16).boundary,'linewidth',2)
hold off