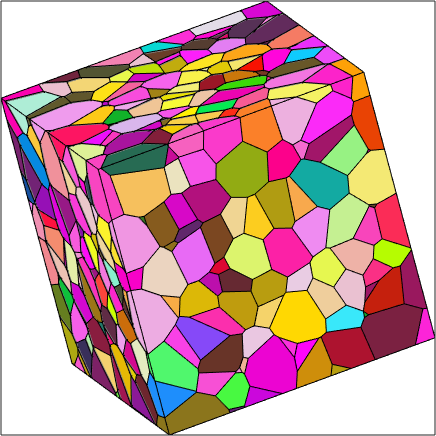
On this page we explain some basic operations with three dimensional grains. Let us start by importing some example data set and plot it from a nice perspective
mtexdata NeperGrain3d
% colorize by mean orientation
plot(grains,grains.meanOrientation)
setCamera(plottingConvention.default3D)grains = grain3d
Phase Grains Volume Mineral Symmetry Crystal reference frame
2 1000 1e+06 Quartz 321 X||a*, Y||b, Z||c*
boundary faces: 7163
Properties: meanRotation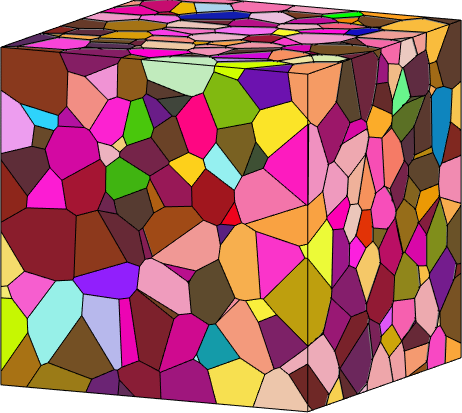
Slicing
We can extract from 3d grain data 2d grain data by slicing them along one or multiple planes. This is done using the command slice. This command requires two inputs to characterize a plane - the plane normal N and an arbitrary point P0 within the plane.
% a point where the slice should pass through
P0 = vector3d(50,50,50);
% the normal direction of the slice
N = vector3d(1,-1,1);
% compute the slice
grains1_10 = grains.slice(N,P0)
% visualize the slice
plot(grains1_10,grains1_10.meanOrientation,'micronbar','off')
setCamera(plottingConvention.default3D)grains1_10 = grain2d
Phase Grains Pixels Mineral Symmetry Crystal reference frame
2 179 179 Quartz 321 X||a*, Y||b, Z||c*
boundary segments: 540 (3153 µm)
inner boundary segments: 0 (0 µm)
triple points: 310
Properties: meanRotation, Id3d
We may adjust the @plottingConvention such that the normal direction is perpendicular to the screen.
how2plot = plottingConvention;
how2plot.outOfScreen = N;
how2plot.north = zvector
setCamera(how2plot)how2plot = plottingConvention
outOfScreen: (4,-7,0)
north : (0,0,1)
east : (7,4,0)
We may use the exact same syntax to generate multiple slices.
N = vector3d.Z;
for k = 1:19:99
grainSlice = grains.slice(N, vector3d(0,0,k));
plot(grainSlice,grainSlice.meanOrientation)
hold on
end
hold off
setCamera(plottingConvention.default3D)Warning: still can not concatenate grains on different slices
Warning: still can not concatenate grains on different slices
Warning: still can not concatenate grains on different slices
Triangulation
Some functions are much faster on triangulated meshes. Therefore you can triangulate your grains with the command triangulate.
grainsTri = grains(20:21).triangulate
plot(grainsTri,grainsTri.meanOrientation)grainsTri = grain3d
Phase Grains Volume Mineral Symmetry Crystal reference frame
2 2 1742 Quartz 321 X||a*, Y||b, Z||c*
boundary faces: 100
Id Phase Pixels meanRotation
20 2 1 (94.3°,43.1°,221.4°)
21 2 1 (136.3°,35.1°,264.8°)
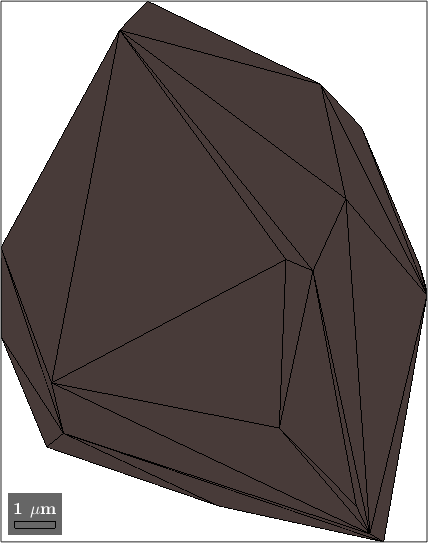
Rotation
Not surprisingly we can use the command rotate to apply any rotation to three dimensional grains. Note that a rotation changes the spatial coordinates as well as the orientation of the grains.
rot = rotation.byAxisAngle(vector3d(1,1,1),30*degree);
grains_rot = rot * grains; % or rotate(grains3,rot)
% plotting
plot(grains_rot,grains_rot.meanOrientation)