MTEX offers several ways to compute average material tensors from ODFs or EBSD data. We start by importing some EBSD data of Glaucophane and Epidote.
% set up a nice colormap
setMTEXpref('defaultColorMap',blue2redColorMap);
% import some EBSD data
ebsd = EBSD.load([mtexDataPath '/EBSD/data.ctf'],...
'convertEuler2SpatialReferenceFrame');
% visualize a subset of the data
plot(ebsd(inpolygon(ebsd,[2000 0 1400 375])))
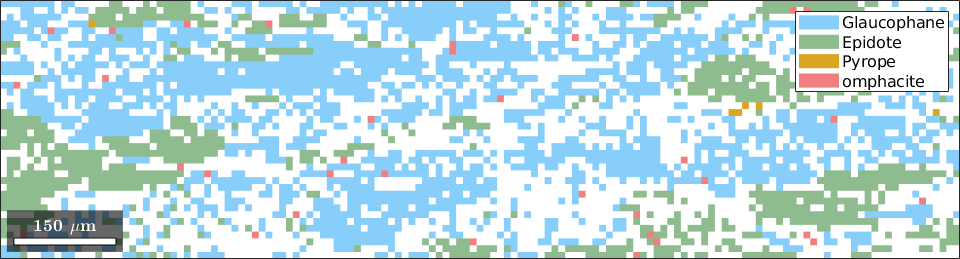
Data Correction
next, we correct the data by excluding orientations with large MAD value
% define maximum acceptable MAD value
MAD_MAXIMUM= 1.3;
% eliminate all measurements with MAD larger than MAD_MAXIMUM
ebsd(ebsd.mad >MAD_MAXIMUM) = []
plot(ebsd(inpolygon(ebsd,[2000 0 1400 375])))ebsd = EBSD
Phase Orientations Mineral Color Symmetry Crystal reference frame
0 28015 (56%) notIndexed
1 13779 (28%) Glaucophane LightSkyBlue 12/m1 X||a*, Y||b*, Z||c
2 4510 (9.1%) Epidote DarkSeaGreen 12/m1 X||a*, Y||b*, Z||c
3 3212 (6.5%) Pyrope Goldenrod m-3m
4 218 (0.44%) omphacite LightCoral 12/m1 X||a*, Y||b*, Z||c
Properties: bands, bc, bs, error, mad
Scan unit : um
X x Y x Z : [0 13290] x [0 370] x [0 0]
Normal vector: (0,0,1)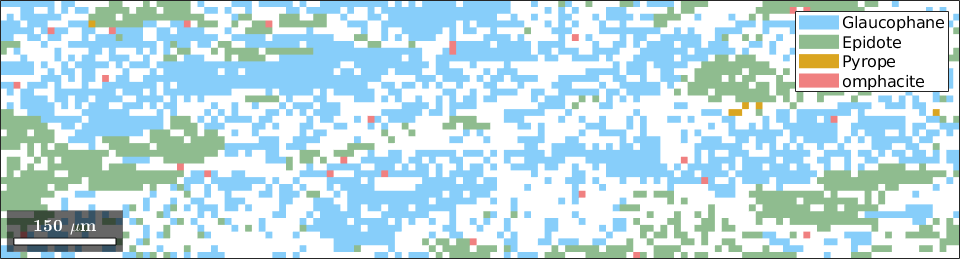
Import the elastic stiffness tensors
The elastic stiffness tensor of Glaucophane was reported in Bezacier et al. 2010 (Tectonophysics) with respect to the crystal reference frame
CS_Tensor_glaucophane = crystalSymmetry('2/m',[9.5334,17.7347,5.3008],...
[90.00,103.597,90.00]*degree,'X||a*','Z||c','mineral','Glaucophane');and the density in g/cm^3
rho_glaucophane = 3.07;by the coefficients \(C_{ij}\) in Voigt matrix notation
Cij = [[122.28 45.69 37.24 0.00 2.35 0.00];...
[ 45.69 231.50 74.91 0.00 -4.78 0.00];...
[ 37.24 74.91 254.57 0.00 -23.74 0.00];...
[ 0.00 0.00 0.00 79.67 0.00 8.89];...
[ 2.35 -4.78 -23.74 0.00 52.82 0.00];...
[ 0.00 0.00 0.00 8.89 0.00 51.24]];The stiffness tensor in MTEX is defined via the command stiffnessTensor.
C_glaucophane = stiffnessTensor(Cij,CS_Tensor_glaucophane,'density',rho_glaucophane);The elastic stiffness tensor of Epidote was reported in Aleksandrov et al. 1974 'Velocities of elastic waves in minerals at atmospheric pressure and increasing the precision of elastic constants by means of EVM (in Russian)', Izv. Acad. Sci. USSR, Geol. Ser.10, 15-24, with respect to the crystal reference frame
CS_Tensor_epidote = crystalSymmetry('2/m',[8.8877,5.6275,10.1517],...
[90.00,115.383,90.00]*degree,'X||a*','Z||c','mineral','Epidote');and the density in g/cm^3
rho_epidote = 3.45;by the coefficients \(C_{ij}\) in Voigt matrix notation
Cij = [[211.50 65.60 43.20 0.00 -6.50 0.00];...
[ 65.60 239.00 43.60 0.00 -10.40 0.00];...
[ 43.20 43.60 202.10 0.00 -20.00 0.00];...
[ 0.00 0.00 0.00 39.10 0.00 -2.30];...
[ -6.50 -10.40 -20.00 0.00 43.40 0.00];...
[ 0.00 0.00 0.00 -2.30 0.00 79.50]];
% And now we define the Epidote stiffness tensor as a MTEX variable
C_epidote = stiffnessTensor(Cij,CS_Tensor_epidote,'density',rho_epidote);The Average Tensor from EBSD Data
The Voigt, Reuss, and Hill averages for all phases are computed by
[CVoigt,CReuss,CHill] = calcTensor(ebsd({'Epidote','Glaucophane'}),C_glaucophane,C_epidote);The Voigt and Reuss are averaging schemes for obtaining estimates of the effective elastic constants in polycrystalline materials. The Voigt average assumes that the elastic strain field in the aggregate is constant everywhere, so that the strain in every position is equal to the macroscopic strain of the sample. CVoigt is then estimated by a volume average of local stiffness C(gi), where gi is the orientation given by a triplet of Euler angles and with orientation gi, and volume fraction V(i). This is formally described as
\( \left<T\right>^{\text{Voigt}} = \sum_{m=1}^{M} T(\mathtt{ori}_{m})\)
The Reuss average on the other hand assumes that the stress field in the aggregate is constant, so the stress in every point is set equal to the macroscopic stress. CReuss is therefore estimated by the volume average of local compliance S(gi) and can be described as
\( \left<T\right>^{\text{Reuss}} = \left[ \sum_{m=1}^{M} T(\mathtt{ori}_{m})^{-1} \right]^{-1}\)
For weakly anisotropic phases (e.g. garnet), Voigt and Reuss averages are very close to each other, but with increasing elastic anisotropy, the values of the Voigt and Reuss bounds vary considerably
The estimate of the elastic moduli of a given aggregate nevertheless should lie between the Voigt and Reuss average bounds, as the stress and strain distributions should be somewhere between the uniform strain (Voigt bound) and uniform stress.
Hill (1952) showed that the arithmetic mean of the Voigt and Reuss bounds (called Hill or Voigt-Reuss-Hill average) is very often close to the experimental values (although there is no physical justification for this behavior).
Averaging the elastic stiffness of an aggregate based on EBSD data
for a single phase (e.g. Glaucophane) the syntax is
[CVoigt_glaucophane,CReuss_glaucophane,CHill_glaucophane] = calcTensor(ebsd('glaucophane'),C_glaucophane);ODF Estimation
Next, we estimate an ODF for the Epidote phase
odf_gl = calcDensity(ebsd('glaucophane').orientations,'halfwidth',10*degree);The Average Tensor from an ODF
The Voigt, Reuss, and Hill averages for the above ODF are computed by
[CVoigt_glaucophane, CReuss_glaucophane, CHill_glaucophane] = ...
calcTensor(odf_gl,C_glaucophane);To visualize the polycrystalline Glaucophane wave velocities we can use the command plotSeismicVelocities
plotSeismicVelocities(CHill_glaucophane)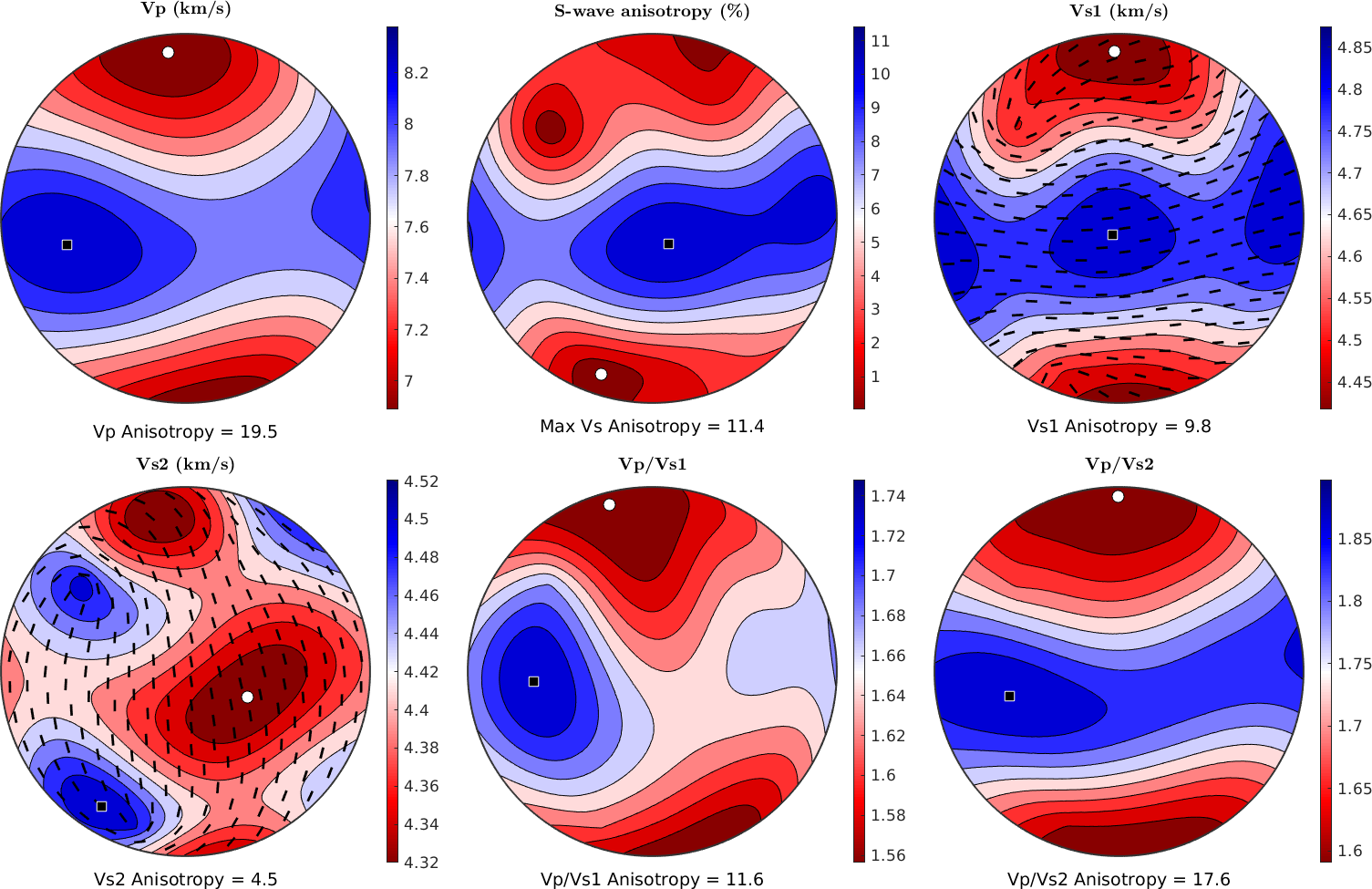
More details on averaging the seismic properties considering the modal composition of different phases can be found in here