Selecting Grains edit page

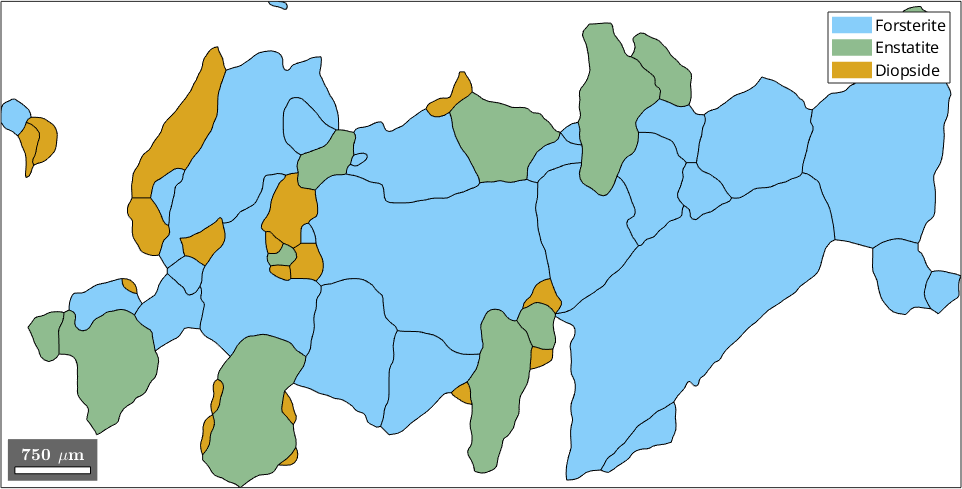
In this section we discuss how to select grains by properties. We start our discussion by reconstructing the grain structure from a sample EBSD data set.

% load sample EBSD data set
mtexdata forsterite silent

% restrict it to a subregion of interest.
ebsd = ebsd(inpolygon(ebsd,[5 2 10 5]*10^3));

% remove all not indexed pixels
ebsd = ebsd('indexed');

% reconstruct grains
[grains, ebsd.grainId] = calcGrains(ebsd,'angle',5*degree,'minPixel',5);

% smooth them
grains = smooth(grains,5);

% plot the orientation data of the Forsterite phase
plot(ebsd('fo'),ebsd('fo').orientations)

% plot the grain boundary on top of it
hold on
plot(grains.boundary,'lineWidth',2)
hold off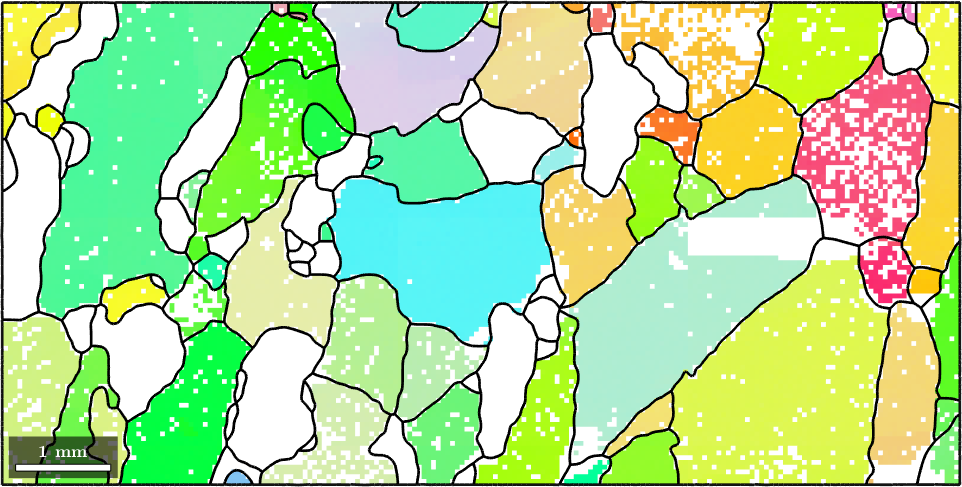

Selecting grains by mouse

The most easiest way to select a grain is by using the mouse and the command selectInteractive which allows you to select an arbitrary amount of grains. The index of the selected grains appear as the global variable indSelected in your workspace

selectInteractive(grains,'lineColor','gold')

% this simulates a mouse click
pause(1)
simulateClick(9000,3500)
pause(1)

global indSelected;
grains(indSelected)

hold on
plot(grains(indSelected).boundary,'lineWidth',4,'lineColor','gold')
hold off
Grain selected: 74
 
ans = grain2d (y↑→x)
 
 Phase  Grains  Pixels     Mineral  Symmetry  Crystal reference frame
     1       1     451  Forsterite       mmm                         
 
 boundary segments: 136 (5856 µm)
 inner boundary segments: 0 (0 µm)
 triple points: 8
 
 Id   Phase   Pixels      meanRotation         GOS
 74       1      451   (50°,162°,328°)   0.0129712

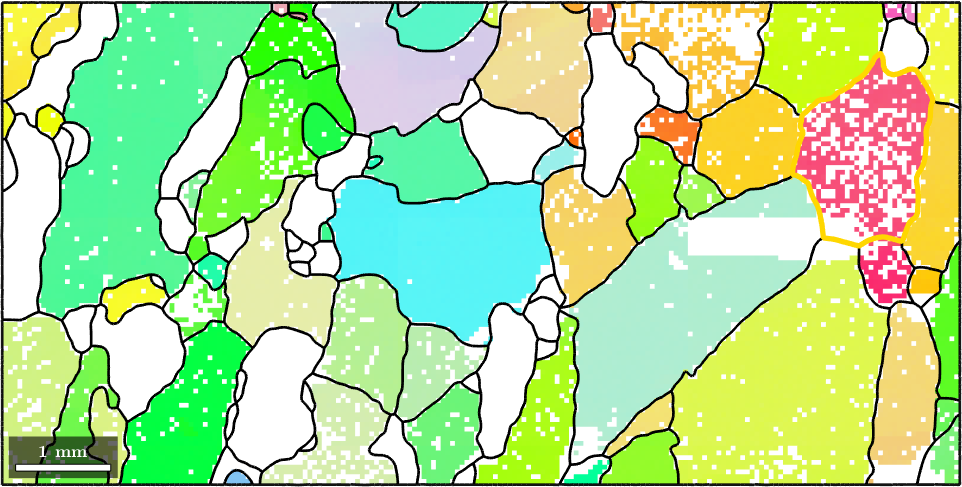
Indexing by orientation or position

One can also to select a grain by spatial coordinates without user interaction. This is done using the syntax grains(x,y), i.e.,

x = 12000; y = 4000;

hold on
plot(grains(x,y).boundary,'linewidth',4,'linecolor','blue')

plot(x,y,'marker','s','markerfacecolor','k',...
  'markersize',10,'markeredgecolor','w')
hold off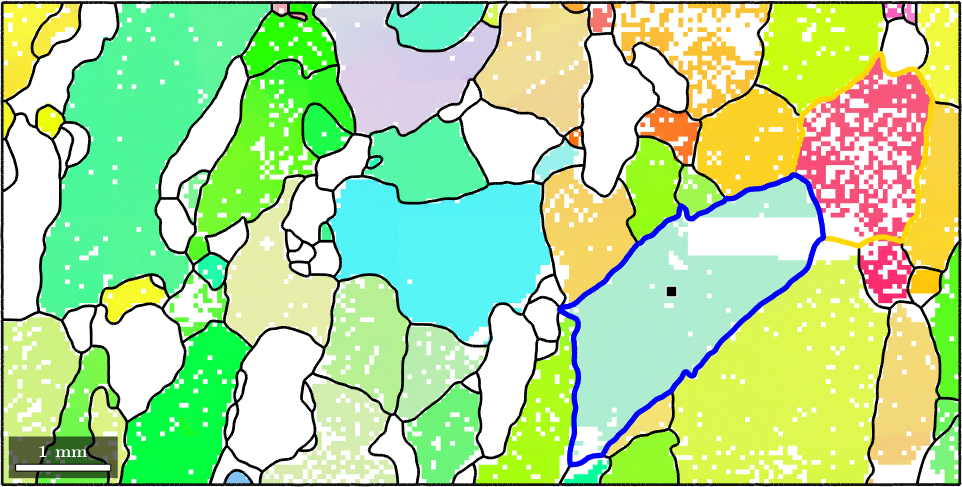

Alternatively one can also select all grains with a certain orientation. Lets find all grains with a similar orientation as the one marked in gold. As threshold we shall use 20 degree

% select grains by orientation
grains_selected = grains.findByOrientation(grains(indSelected).meanOrientation,20*degree)

hold on
plot(grains_selected.boundary,'linewidth',4,'linecolor','gold')
hold off
grains_selected = grain2d (y↑→x)
 
 Phase  Grains  Pixels     Mineral  Symmetry  Crystal reference frame
     1       3     534  Forsterite       mmm                         
 
 boundary segments: 191 (8474 µm)
 inner boundary segments: 9 (267 µm)
 triple points: 13
 
 Id   Phase   Pixels      meanRotation      GOS
 42       1       75   (63°,165°,339°)    0.029
 74       1      451   (50°,162°,328°)    0.013
 94       1        8   (68°,151°,338°)   0.0072

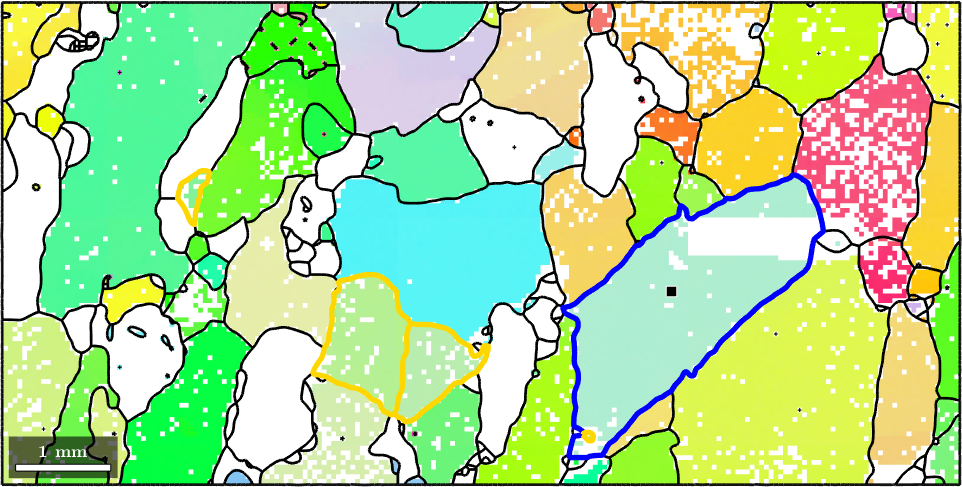
Indexing by a Property

In order the generalize the above concept lets remember that the variable grains is essentially a large vector of grains. Thus when applying a function like area to this variable we obtain a vector of the same length with numbers representing the area of each grain

grain_area = grains.area;

As a first rather simple application we could colorize the grains according to their area, i.e., according to the numbers stored in grain_area 

plot(grains,grain_area)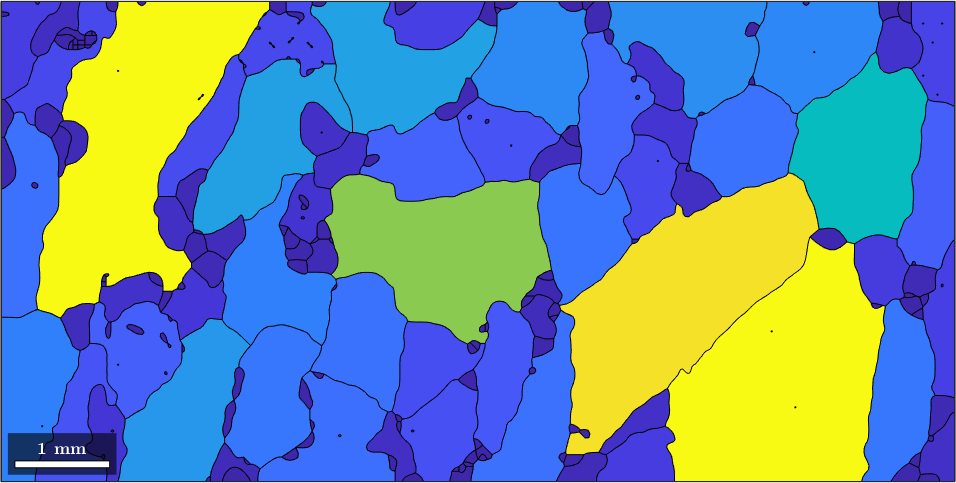

As a second application, we can ask for the largest grain within our data set. The maximum value and its position within a vector are found by the MATLAB command max.

[max_area,max_id] = max(grain_area)
max_area =
   4.1272e+06
max_id =
    38

The number max_id is the position of the grain with a maximum area within the variable grains. We can access this specific grain by direct indexing

grains(max_id)
ans = grain2d (y↑→x)
 
 Phase  Grains  Pixels     Mineral  Symmetry  Crystal reference frame
     1       1    1448  Forsterite       mmm                         
 
 boundary segments: 222 (8622 µm)
 inner boundary segments: 0 (0 µm)
 triple points: 5
 
 Id   Phase   Pixels       meanRotation         GOS
 38       1     1448   (166°,127°,259°)   0.0135419

and so we can plot it

hold on
plot(grains(max_id).boundary,'linecolor','red','linewidth',4)
hold off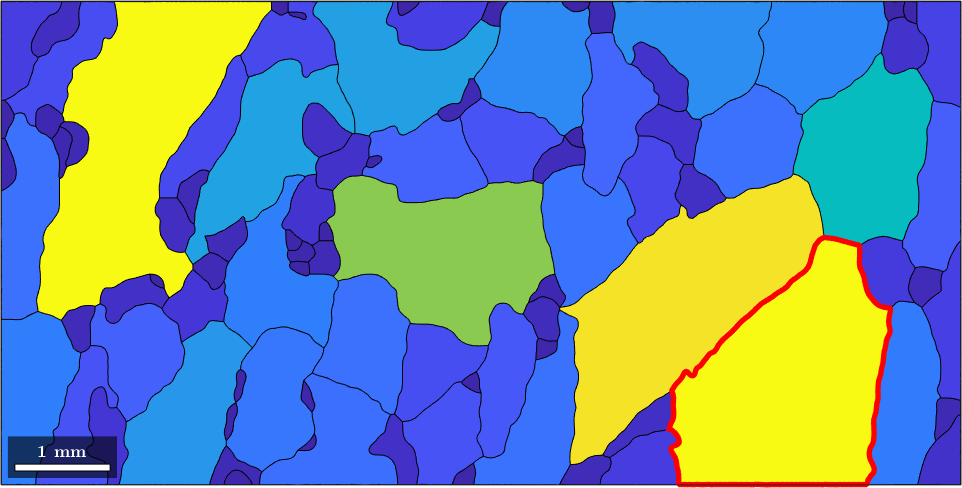

Note that this way of addressing individual grains can be generalized to many grains. E.g. assume we are interested in the largest 5 grains. Then we can sort the vector grain_area and take the indices of the 5 largest grains.

[sorted_area,sorted_id] = sort(grain_area,'descend');

large_grain_id = sorted_id(2:5);

hold on
plot(grains(large_grain_id).boundary,'linecolor','Orange','linewidth',4)
hold off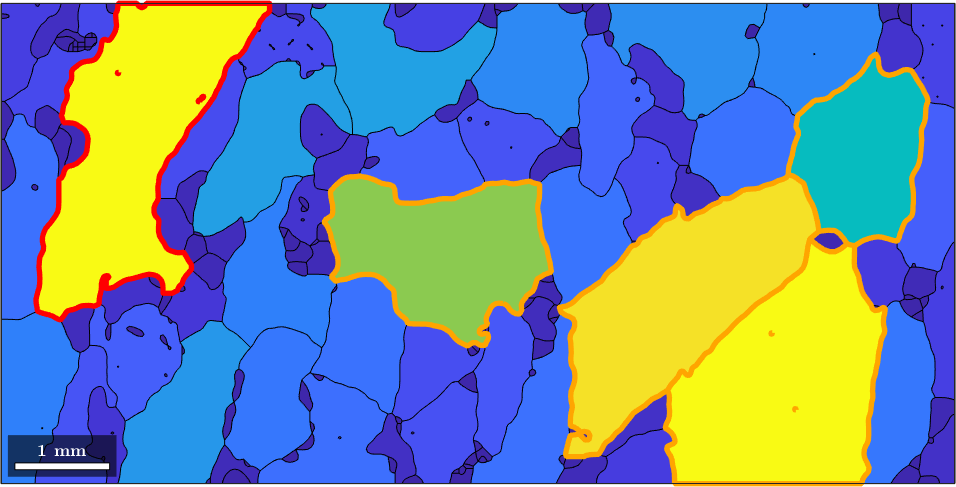

Indexing by a Condition

By the same syntax as above we can also single out grains that satisfy a certain condition. I.e., to access are grains that are at least one quarter as large as the largest grain we can do

condition = grain_area > max_area/4;

hold on
plot(grains(condition).boundary,'linecolor','Yellow','linewidth',4)
hold off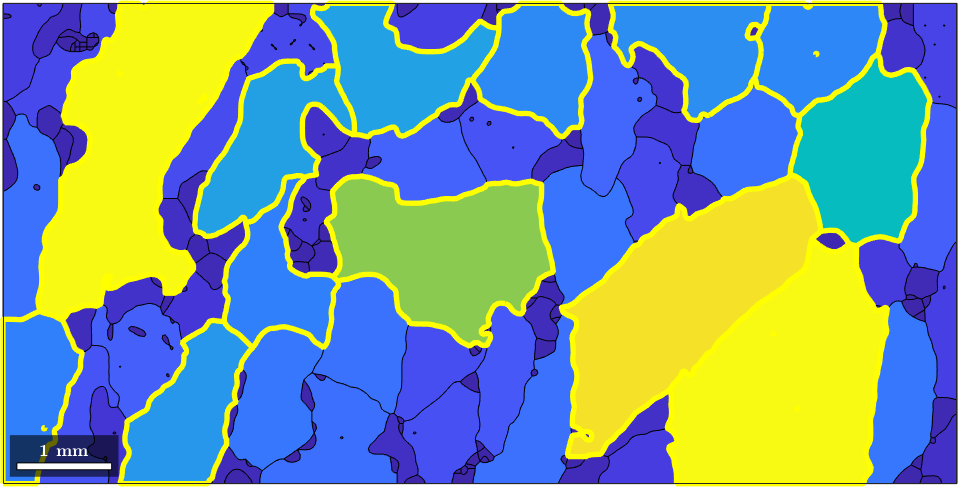

This is a very powerful way of accessing grains as the condition can be build up using any grain property. As an example let us consider the phase. The phase of the first five grains we get by

grains(1:5).phase
ans =
     1
     3
     1
     3
     3

Now we can access or grains of the first phase Forsterite by the condition

condition = grains.phase == 1;
plot(grains(condition))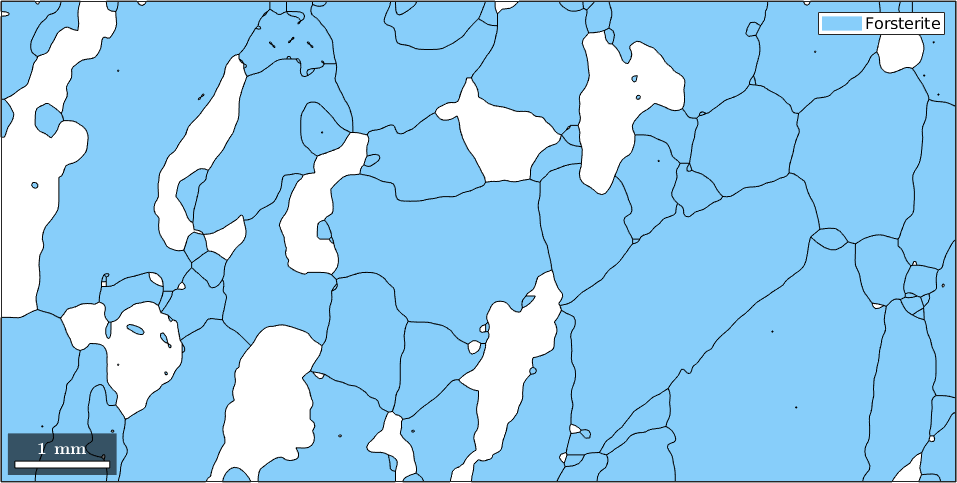

To make the above more directly you can use the mineral name for indexing

grains('forsterite')
ans = grain2d (y↑→x)
 
 Phase  Grains  Pixels     Mineral  Symmetry  Crystal reference frame
     1      61   14010  Forsterite       mmm                         
 
 boundary segments: 3543 (134904 µm)
 inner boundary segments: 15 (317 µm)
 triple points: 136
 
 Properties: meanRotation, GOS

Logical indexing allows also for more complex queries, e.g. selecting all grains perimeter larger than 6000 and at least 600 measurements within

condition = grains.perimeter>6000 & grains.numPixel >= 600;

selected_grains = grains(condition)

plot(selected_grains)
selected_grains = grain2d (y↑→x)
 
 Phase  Grains  Pixels     Mineral  Symmetry  Crystal reference frame
     1       4    5248  Forsterite       mmm                         
 
 boundary segments: 886 (34740 µm)
 inner boundary segments: 0 (0 µm)
 triple points: 43
 
 Id   Phase   Pixels       meanRotation      GOS
 38       1     1448   (166°,127°,259°)    0.014
 47       1     1047     (89°,99°,224°)   0.0077
 50       1     1208    (153°,68°,237°)   0.0081
 82       1     1545    (167°,81°,251°)    0.013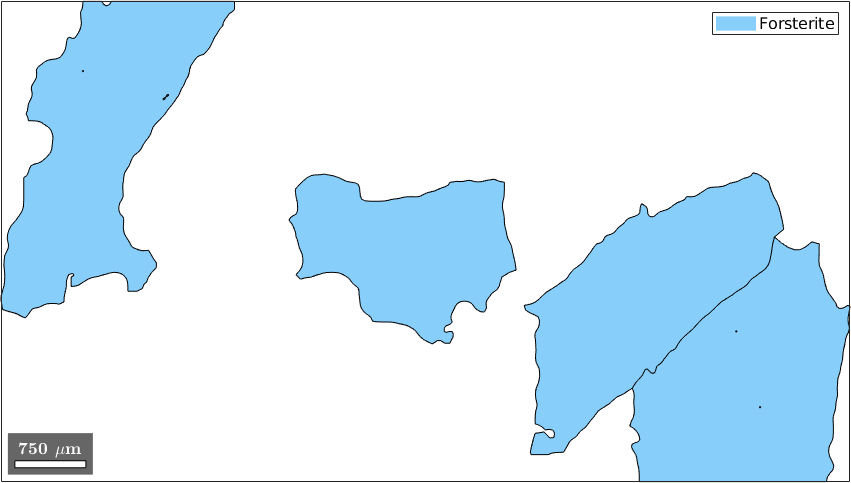

The grainId and how to select EBSD inside specific grains

Besides, the list of grains the command calcGrains returns also two other output arguments.

plot(grains)
largeGrains = grains(grains.numPixel > 50);

text(largeGrains,largeGrains.id)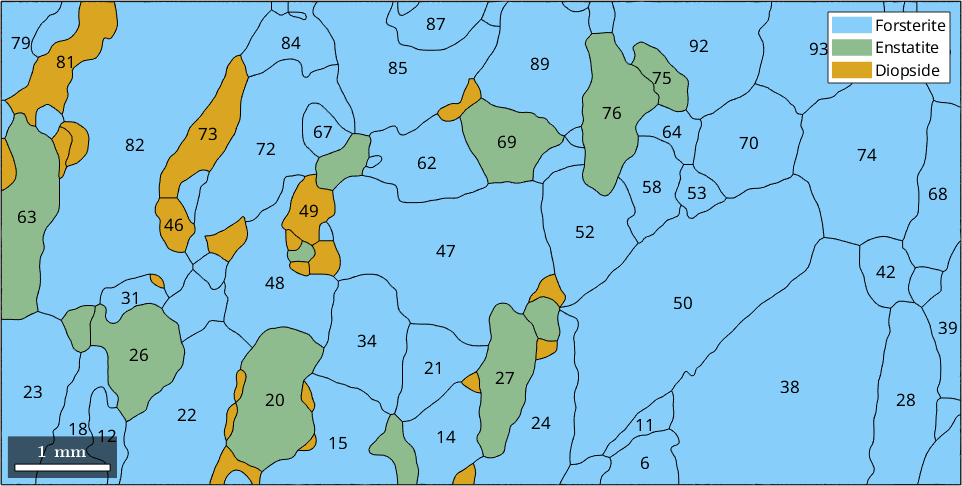

The second output argument grainId is a list with the same size as the EBSD measurements that stores for each measurement the corresponding grainId. The above syntax stores this list directly inside the ebsd variable. This enables MTEX to select EBSD data by grains. The following command returns all the EBSD data that belong to grain number 33.

ebsd(grains(33))
ans = EBSD (y↑→x)
 
 Phase  Orientations     Mineral         Color  Symmetry  Crystal reference frame
     1     42 (100%)  Forsterite  LightSkyBlue       mmm                         
 
 Properties: bands, bc, bs, error, mad, grainId
 Scan unit : um
 X x Y x Z : [6750 7300] x [3550 4150] x [0 0]
 Normal vector: (0,0,1)

and is equivalent to the command

ebsd(ebsd.grainId == 33)
ans = EBSD (y↑→x)
 
 Phase  Orientations     Mineral         Color  Symmetry  Crystal reference frame
     1     42 (100%)  Forsterite  LightSkyBlue       mmm                         
 
 Properties: bands, bc, bs, error, mad, grainId
 Scan unit : um
 X x Y x Z : [6750 7300] x [3550 4150] x [0 0]
 Normal vector: (0,0,1)

The following picture plots the largest grains together with its individual orientation measurements.

plot(ebsd(grains(max_id)),ebsd(grains(max_id)).orientations)
hold on
plot(grains(max_id).boundary,'lineWidth',2)
hold off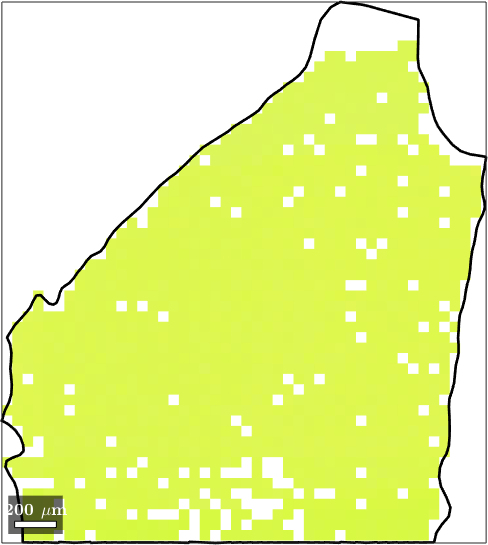

Boundary grains

Sometimes it is desirable to remove all boundary grains as they might distort grain statistics. To do so one should remember that each grain boundary has a property grainId which stores the ids of the neighboring grains. In the case of an outer grain boundary, one of the neighboring grains has the id zero. We can filter out all these boundary segments by

% ids of the outer boundary segment
outerBoundary_id = any(grains.boundary.grainId==0,2);

% plot the outer boundary segments
plot(grains)
hold on
plot(grains.boundary(outerBoundary_id),'linecolor','red','linewidth',2)
hold off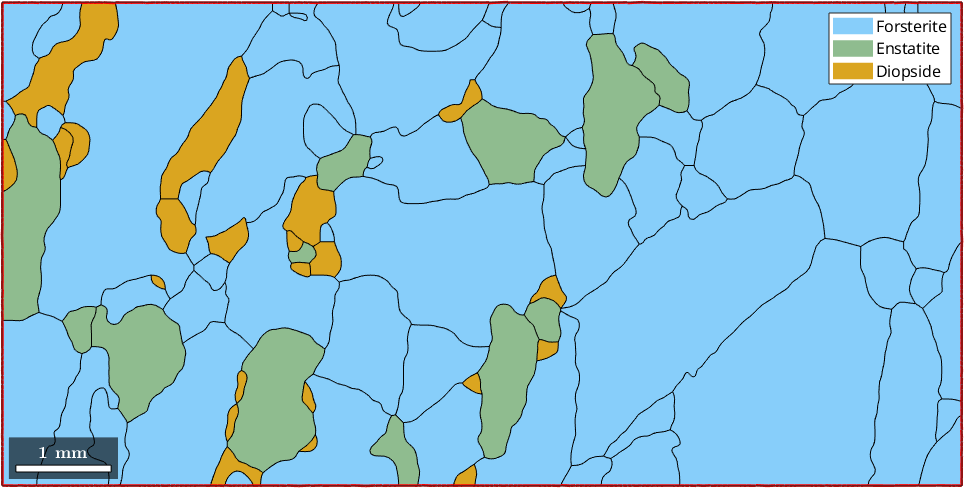

Now grains.boundary(outerBoundary_id).grainId is a list of grain ids where the first column is zero, indicating the outer boundary, and the second column contains the id of the boundary grain. Hence, it remains to remove all grains with these ids.

% next we compute the corresponding grain_id
grain_id = grains.boundary(outerBoundary_id).grainId;

% remove all zeros
grain_id(grain_id==0) = [];

% and plot the boundary grains
plot(grains(grain_id))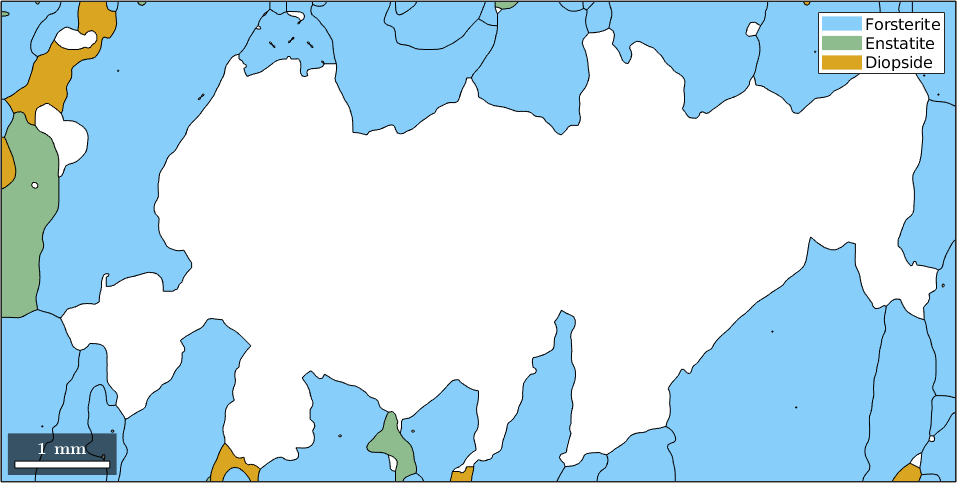

finally, we could remove the boundary grains by

grains(grain_id) = []

However, boundary grains can be selected more easily be the command isBoundary.

plot(grains(~grains.isBoundary))