Spherical Harmonics edit page

The spherical harmonics are special functions on the 2-sphere \(\mathbb S^2\). In terms of polar coordinates \({\bf \xi} = (\sin \theta \cos \rho, \sin \theta \sin \rho, \cos \theta)\) the spherical harmonic of degree \(m\) and order \(l\) is defined by

\[ Y_m^l({\bf \xi}) = \sqrt{\frac{2m+1}{4\pi}}P_m^{|l|}(\cos\rho)\mathrm e^{\mathrm i l\theta} \]

where \(P_m^{|l|}\), \(m \in {\bf N_0}\), and \( l = -m, \ldots m\) denote the associated Legendre-Polynomials.

We get the function values of the spherical harmonics of degree 1 in a point v by the command sphericalY, i.e.

v = vector3d.X
sphericalY(1,v)
v = vector3d
  x y z
  1 0 0
ans =
    0.3455    0.0000    0.3455

The spherical harmonics form an orthonormal basis in \(L_2(\mathbb S^2)\). Hence we describe functions on the 2-sphere by there harmonic representation using the class S2FunHarmonic.

With that we define the spherical harmonic \(Y_1^1\) by

Y = S2FunHarmonic([0;0;0;1])
Y.eval(v)
Y = S2FunHarmonic
  bandwidth: 1
 
ans =
    0.3455

Various normalizations for the sperical harmonics are common in the literature.

Here we define the \(L_2\)-norm by

\[ \| f \|_2 = \left(\int_{\mathrm{sphere}} \lvert f(\xi)\rvert^2 \,\mathrm d\xi\right)^{1/2} \]

such that \( \| 1 \|_2^2 = 1\). Take a look on the section Integration of S2Fun's.

Using that definition the spherical harmonics in MTEX fulfill

\[\| Y_m^l \|_2 = 1\] for all \(m,l\).

norm(Y)
ans =
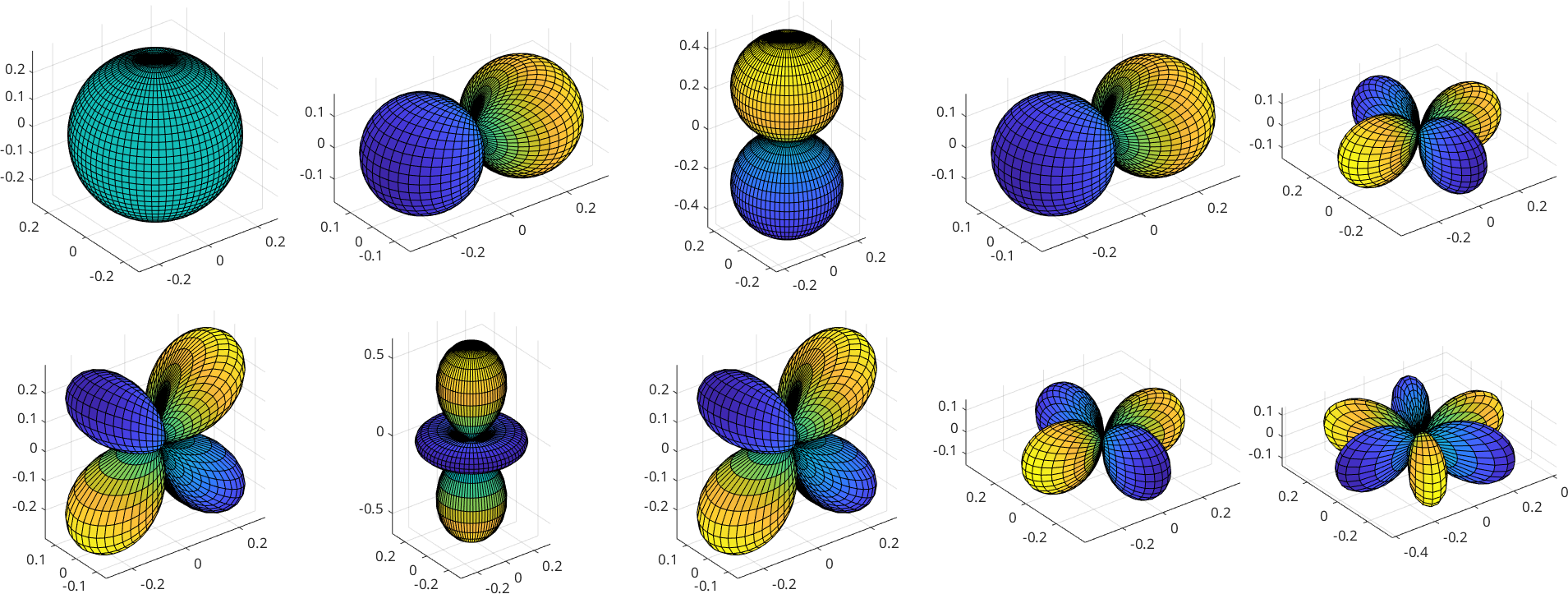
     1

To concluse this section we plot the first ten spherical harmonics

surf(S2FunHarmonic(eye(10)))