Crystal symmetries are sets of rotations and mirroring operations that leave the lattice of a crystal invariant. They form the so called "groups" since the concatenation of two symmetry operations is again a symmetry operation.
Depending which symmetry operations are considered, the symmetry groups are categorized either into 230 space groups, 32 point groups or 11 Laue groups.
Purely enantiomorphic (rotational) symmetry groups
There exist exactly 11 symmetry groups consisting of proper rotations only, namely, 1, 2, 222, 3, 23, 4, 422, 6, 622, 32, 432. These are the so called enantiomorphic groups. All the groups can be defined in MTEX either by its international notation
cs = crystalSymmetry('432')cs = crystalSymmetry
symmetry: 432
elements: 24
a, b, c : 1, 1, 1or by the Schoenflies notation
cs = crystalSymmetry('O')
plot(cs)cs = crystalSymmetry
symmetry: 432
elements: 24
a, b, c : 1, 1, 1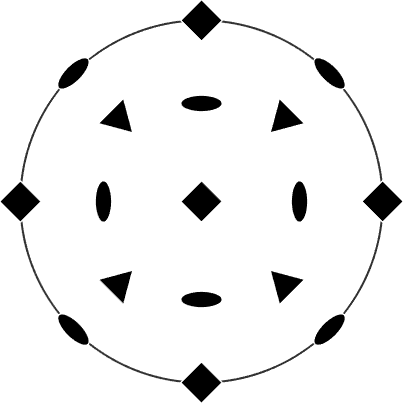
Laue groups
For any symmetry group we obtain the corresponding Laue group by adding the inversion as an additional symmetry element.
csLaue = union(cs,rotation.inversion)
plot(csLaue)csLaue = crystalSymmetry
symmetry: m-3m
elements: 48
a, b, c : 1, 1, 1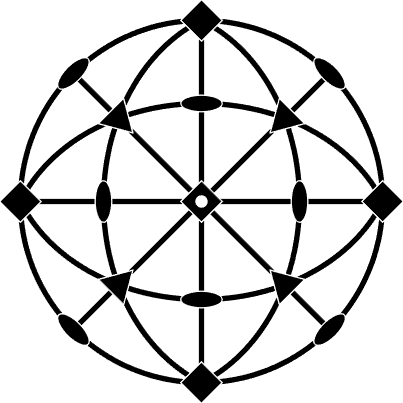
More directly, the Laue group corresponding to an arbitrary point group can be defined by the command
cs.Laueans = crystalSymmetry
symmetry: m-3m
elements: 48
a, b, c : 1, 1, 1Since all Laue groups can be derived from the 11 enantiomorphic groups there are also 11 Laue groups, namely -1, 2/m, mmm, -3, -3m, -4/m, 4/mmm, 6/m, 6/mmm, m-3, m-3m.
The Laue groups have always exactly twice as many symmetry elements as the corresponding enantiomorphic group. As the following example illustrates, each symmetry element from the enantiomorphic group occurs twice - with and without inversion - in the corresponding Laue group.
cs = crystalSymmetry('222');
rotation(cs)
rotation(cs.Laue)ans = rotation
size: 2 x 2
Bunge Euler angles in degree
phi1 Phi phi2
0 0 0
45 180 45
180 0 0
45 180 225
ans = rotation
size: 4 x 2
Bunge Euler angles in degree
phi1 Phi phi2 Inv.
0 0 0 0
45 180 45 0
180 0 0 0
45 180 225 0
0 0 0 1
45 180 45 1
180 0 0 1
45 180 225 1Point groups
While the enantiomorphic groups contain exclusively proper rotations and Laue groups contain a proper and an improper version of each rotation, there are also symmetry groups with improper rotations that do not contain the inversion, e.g. the point group mm2
cs = crystalSymmetry('mm2')
rotation(cs)
plot(cs)cs = crystalSymmetry
symmetry: mm2
elements: 4
a, b, c : 1, 1, 1
ans = rotation
size: 2 x 2
Bunge Euler angles in degree
phi1 Phi phi2 Inv.
0 0 0 0
45 180 45 1
180 0 0 0
45 180 225 1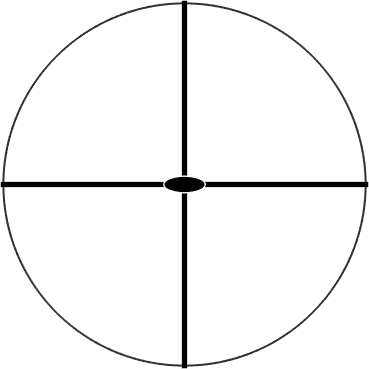
We observe that mm2 has exactly the same rotations as 222 with the only difference that half of them are improper. In fact, we can derive all remaining 10 point groups by replacing half of the rotations of a enantiomorphic group by its improper version. This way the following point groups can be constructed: m, mm2, 3m, -4, 4m2, -42m, -6, 6mm, -6m2, -43m. In total this gives us 11 enantiomorphic + 11 Laue + 10 mixed = 32 point groups.
In MTEX we may use the following commands to find the corresponding enantiomorphic group and the corresponding Laue group to any mixed group
cs = crystalSymmetry('-4m2')
mtexFigure('layout',[1 3]);
plot(cs)
mtexTitle(char(cs,'LaTex'))
nextAxis
plot(cs.properGroup)
mtexTitle(char(cs.properGroup,'LaTex'))
nextAxis
plot(cs.Laue)
mtexTitle(char(cs.Laue,'LaTex'))cs = crystalSymmetry
symmetry: -4m2
elements: 8
a, b, c : 1, 1, 1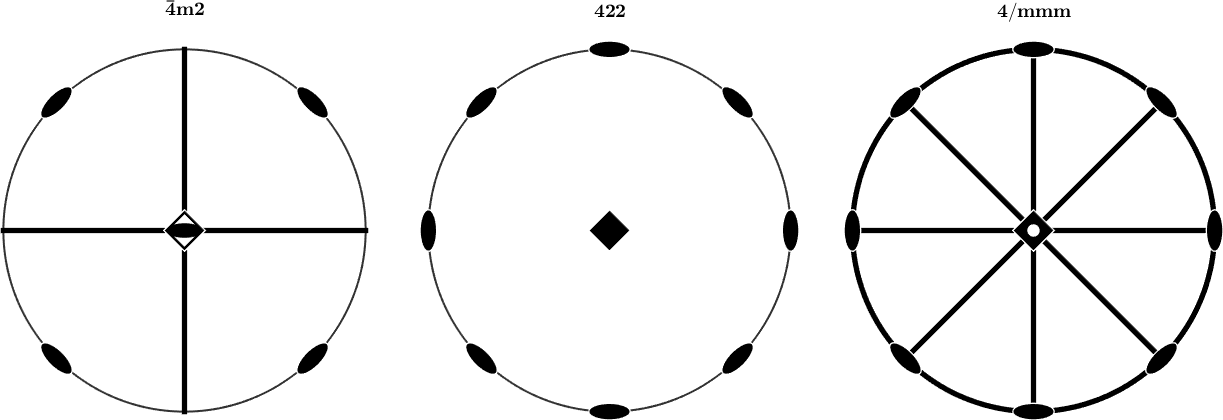
The Subgroup of proper rotations
The enantiomorphic group of a given point group is in general not an subgroup, i.e., it does contain symmetry elements that do not belong to the original point group. If one is interested in the subgroup of proper rotations of a given point group the following command comes into help
plot(cs.properSubGroup)
mtexTitle(char(cs.properSubGroup,'LaTex'))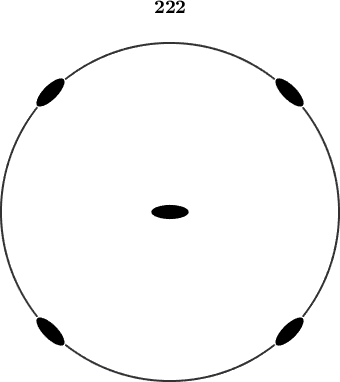
Alignment of the symmetry operations
Although in general only 32 point groups are distinguished, some of them allow for different alignments of the symmetry operations with respect to the crystal axes. The following plots show three different alignments of the point group 2mm. Note that the a-axis points in all three case towards south.
mtexFigure('layout',[1 3]);
cs = crystalSymmetry('2mm');
plot(cs)
mtexTitle(char(cs,'LaTex'))
annotate(cs.aAxis,'labeled')
nextAxis
cs = crystalSymmetry('m2m');
plot(cs)
mtexTitle(char(cs,'LaTex'))
annotate(cs.aAxis,'labeled')
nextAxis
cs = crystalSymmetry('mm2');
plot(cs)
mtexTitle(char(cs,'LaTex'))
annotate(cs.aAxis,'labeled')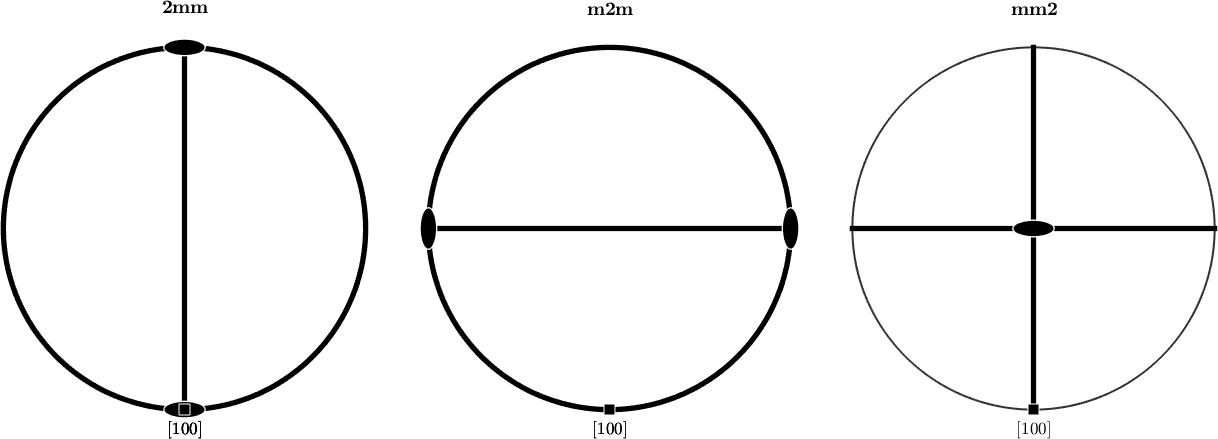
Similarly as with mm2, there are different alignments for the point groups 112, 121, 211, 11m, 1m1, m11, 321, 312, 3m1, 31m, etc.
Space groups
If additionally to the proper and improper rotations also translations are considered as symmetry operations the number of different symmetry groups increases to 320. Those are exhaustively described in the international table of crystallography.
MTEX currently does not support space groups. If the name of a space group os passed to the command crystalSymmetry, MTEX automatically determines the corresponding point group and assigns it to the variable.
cs = crystalSymmetry('Td');
plot(cs)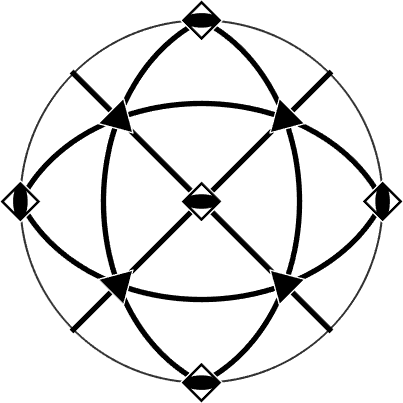
Computations with symmetries
Using the commands union and disjoint new symmetries can be computed from two given ones
union(crystalSymmetry('23'),crystalSymmetry('4'))
disjoint(crystalSymmetry('432'),crystalSymmetry('622'))ans = crystalSymmetry
symmetry: 432
elements: 24
a, b, c : 1, 1, 1
ans = crystalSymmetry
symmetry: 222
elements: 4
a, b, c : 1, 1, 1Import from CIF and PHL files
MTEX allows to define a crystal symmetry by importing a crystallographic information file (*.cif)
cs = crystalSymmetry.load('quartz')cs = crystalSymmetry
mineral : Quartz
symmetry : 321
elements : 6
a, b, c : 4.9, 4.9, 5.4
reference frame: X||a*, Y||b, Z||c*or a Bruker .phl file. As a .phl file contains usually many phases the output is a list of crystal symmetries
% import a list of crystal symmetries
cs_list = crystalSymmetry.load('crystal.phl');
% access the first symmetry in list
cs_list{1}ans = crystalSymmetry
mineral : Magnetite
symmetry: m-3m
elements: 48
a, b, c : 8.4, 8.4, 8.4