Syntax

[v,pos] = max(SO3F) % the position where the maximum is atained

[v,pos] = max(SO3F,'numLocal',5) % the 5 largest local maxima

SO3F = max(SO3F, c) % maximum of a rotational functions and a constant
SO3F = max(SO3F1, SO3F2) % maximum of two rotational functions
SO3F = max(SO3F1, SO3F2, 'bandwidth', bw) % specify the new bandwidth

% global maximum of each component of a vector valued function
[v,pos] = max(SO3Fmulti)

% compute the maximum of a vector valued function along dim
SO3F = max(SO3Fmulti,[],dim)

Input

`SO3F, SO3F1, SO3F2`	`SO3Fun`
`SO3Fmulti`	`a vector valued SO3Fun`
`c`	`double`

Output

`v`	`double`
`pos`	`rotation / orientation`

Options

`kmax`	`number of iterations`
`numLocal`	`number of peaks to return`
`startingNodes`	`rotation / orientation`
`tolerance`	`minimum distance between two peaks`
`resolution`	`minimum step size`
`maxStepSize`	`maximum step size`

Flags

`gradDescent`	`use gradient Descent (slower)`
`noNFFT`	`(together with 'gradDescent') prevent usage of NFFT-methods by direct summation (slow, but computable for very high bandwiths if matlab brokes in other cases)`

Example

%find the local maxima of the <SantaFe.html SantaFe> ODF
[value,ori] = max(SantaFe)
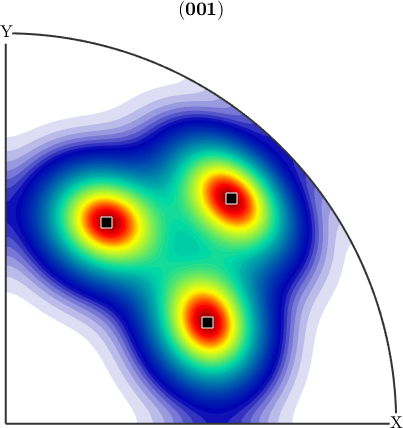
plotPDF(SantaFe,Miller(0,0,1,ori.CS))
annotate(ori)

value =
    5.0394
 
ori = orientation (m3̅m → y↑→x (222))
 
  Bunge Euler angles in degree
     phi1     Phi    phi2
  153.361  48.232  243.45

Citing this page. This page is part of the documentation of MTEX, a free and open source MATLAB toolbox for analyzing and modeling crystallographic textures. It was written by The MTEX Developers and is published at https://mtex-toolbox.github.io/SO3FunHarmonic.max.html. If you use MTEX, or reuse text or figures from this page, in your research, please cite

F. Bachmann, R. Hielscher, H. Schaeben: Texture Analysis with MTEX - Free and Open Source Software Toolbox, Solid State Phenomena 160 (2010), 63-68. 10.4028/www.scientific.net/SSP.160.63

BibTeX

@article{bachmann2010mtex,
  author  = {F. Bachmann and R. Hielscher and H. Schaeben},
  title   = {Texture Analysis with MTEX - Free and Open Source Software Toolbox},
  journal = {Solid State Phenomena},
  volume  = {160},
  pages   = {63-68},
  year    = {2010},
  doi     = {10.4028/www.scientific.net/SSP.160.63},
  url     = {https://doi.org/10.4028/www.scientific.net/SSP.160.63}
}

Other papers describing specific MTEX methods are listed under Publications — please cite the one that best fits your application. The MTEX source code is licensed under the GNU General Public License v2.0; the text and figures of this documentation are licensed under CC BY 4.0, which permits reuse — including by automated systems — provided The MTEX Developers and this page are credited.

SO3FunHarmonic.max