of Materials Engineering, Germany
Data Import
The following EBSD maps has been measured by Ruben Wagner TUBAF, Institute of Materials Engineering, 2022 within the project SFB 920. It shows an alumina inclusions in 42CrMo4 steel after nanoindentation.
% set crystal symmetry
cs = crystalSymmetry.load('Al2O3-Corundum.cif');
% set plotting convention
setMTEXpref('xAxisDirection','east');
setMTEXpref('zAxisDirection','intoPlane');
% import data
path = [mtexExamplePath filesep 'PlasticityExamples' filesep ];
ebsd = EBSD.load([path 'K1_C_16_EBSD_original_bc.txt'],...
{'notIndexed',cs,'notIndexed'},'interface','csv','silent');
% rotate the data in the right reference frame
rot = rotation.byEuler(90*degree,180*degree,0*degree);
ebsd = rotate(ebsd('indexed'),rot,'keepXY');Initial grain reconstruction and visualization
% reconstruct grain structure
[grains,ebsd.grainId] = calcGrains(ebsd,'angle',1*degree);
cKey = ipfColorKey(cs);
cKey.inversePoleFigureDirection = vector3d(1,0,0);
figure(2)
plot(ebsd,cKey.orientation2color(ebsd.orientations))
hold on
plot(grains.boundary,grains.boundary.misrotation.angle./degree,'linewidth',3)
hold off
mtexColorbar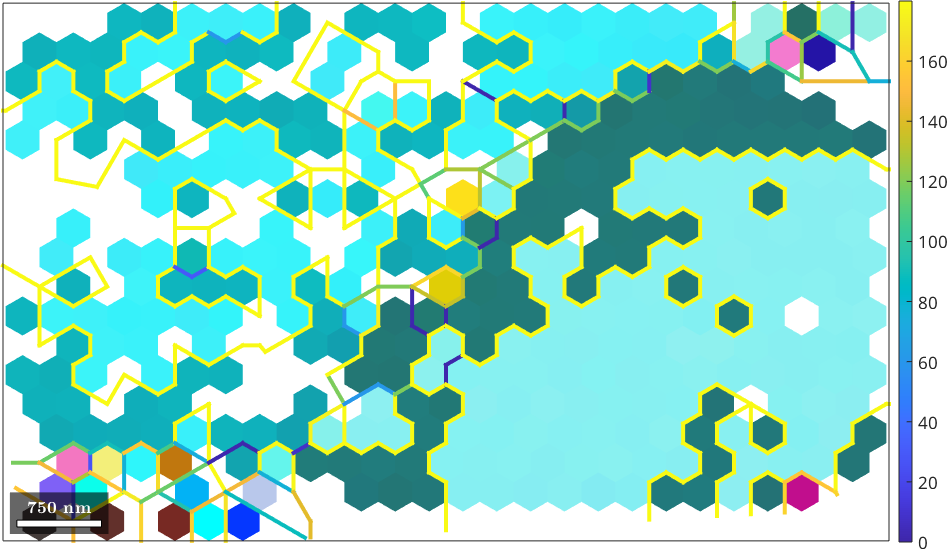
Correct for misindexiation due to pseudosymmetry
Looking at the raw data we observe several neighbouring measurements that are exactly 180 degree rotated with respect to each other. This is indicated by color coded grain boundaries. It is suspected that this misorientation occurs as the EBSD system has a hard time to distinguish the Kikuchi pattern of two orientations that differ by a rotation about the c-axis by 180 degree.
In order to correct for this misindexiation we proceed as follows
# Identify grain boundaries due to pseudo symmetry # Merge grains with common pseudo symmetry grain boundaries and compute the dominant orientation of the merged grains # Correct the EBSD data according to the pseudo symmetry
1. Identify boundaries between pseudosymmetric grains
% all Corundum Corundum boundaries
gB = grains.boundary('indexed');
% define the pseudo symmetry
pseudoSym = orientation.byAxisAngle(cs.cAxis,180*degree);
% allow for a three 3 degree threshold
ispseudoBnd = angle(gB.misorientation,pseudoSym)<3*degree;2. Merge grains with common pseudo symmetry grain boundaries This results is two big grains as visualised below
[grains, parentId] = grains.merge(gB(ispseudoBnd),'calcMeanOrientation',...
@(g) updateOri(g,pseudoSym));
plot(grains,cKey.orientation2color(grains.meanOrientation))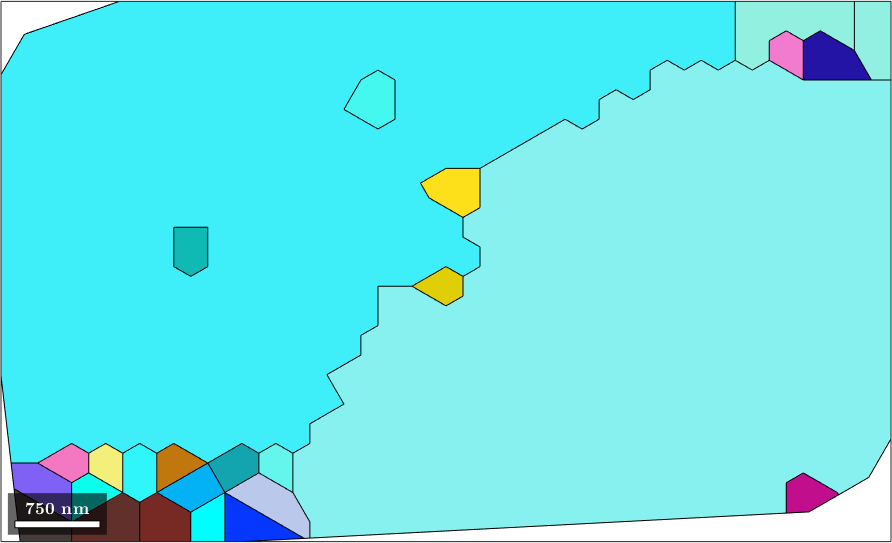
3. Correct the EBSD data according to the pseudo symmetry
% find all EBSD data which differ by the computed grain orientation by
% about 180 degree
flipPseudo = ~(angle(ebsd.orientations,grains(parentId(ebsd.grainId)).meanOrientation)> 10*degree);
ebsd(flipPseudo).orientations = ebsd(flipPseudo).orientations * pseudoSym;
cKey.inversePoleFigureDirection = zvector;
plot(ebsd,cKey.orientation2color(ebsd.orientations))
Data cleaning
We perform some more data cleaning steps including
- removing too small grains
- filling of the not indexed pixels
% redo grain reconstruction
[grains,ebsd.grainId] = calcGrains(ebsd,'angle',1*degree);
% and remove little grains
ebsd(grains(grains.grainSize<4)) = [];
[grains,ebsd.grainId] = calcGrains(ebsd,'angle',1*degree);
% filling EBSD holes
F = halfQuadraticFilter;
F.alpha=0.3;
ebsdS = smooth(ebsd,F,'fill',grains);
% visualize the result
cKey.inversePoleFigureDirection = zvector;
plot(ebsdS,cKey.orientation2color(ebsdS.orientations))
hold on
plot(ebsd, ebsd.bc,'FaceAlpha',0.3)
colormap gray % make the image grayscale
mtexColorbar
hold off
Schmid Factor Analysis
Next we compute the the active slip system during pressure in z-direction. The possible dominant slip systems in alumina are described in Mao2011 and 2012 as
n = Miller(1,0,-1,1,cs,'HKIL');
b = Miller(-1,2,-1,0,cs,'UVTW');
sS = slipSystem(b,n)sS = slipSystem (Corundum)
U V T W | H K I L CRSS
-1 2 -1 0 1 0 -1 1 1Next we determine the Schmid factor for all symmetrically equivalent slip systems.
% rotate symmetrically equivalent slip systems into specimen coordinates of
% each grain
sSLocal = grains.meanOrientation * sS.symmetrise('antipodal');
% compute Schmid factor according Z axis
sigma = stressTensor.uniaxial(vector3d.Z);
SF = abs(sSLocal.SchmidFactor(sigma));
% sort the slips system according to their Schmid factor from largest to
% smallest
[SF, reorder] = sort(SF,2,"descend");
reorder = sub2ind(size(reorder),repmat((1:size(reorder,1))',1,size(reorder,2)),reorder);
sSLocal = sSLocal(reorder);Finally, we plot the trace of the slip planes together with the slip direction in the EBSD map.
figure(2)
cKey.inversePoleFigureDirection = zvector;
plot(ebsdS,cKey.orientation2color(ebsdS.orientations))
hold on
plot(ebsd, ebsd.bc,'FaceAlpha',0.3)
colormap gray % make the image grayscale
hold off
order = 1;
hold on
% visualize the trace of the slip plane
quiver(grains,sSLocal(:,order).trace,'color','blue','linewidth',5)
% and the slip direction
quiver(grains,sSLocal(:,order).b,'color','gray','linewidth',5)
hold off
function ori = updateOri(grains,pseudoSym)
ori = grains.meanOrientation;
cId = 1+calcCluster(ori,'weights',grains.grainSize);
% variant 1
[~,isTrue] = max(accumarray(cId(:),grains.grainSize));
% variant 2
%[~,isTrue] = max(accumarray(cId(:),grains.numNeighbors));
ori(cId ~= isTrue) = ori(cId ~= isTrue) * pseudoSym;
ori = mean(ori,'weigths',grains.grainSize,'robust');
end....References
- Ruben Wagner, Robert Lehnert, Enrico Storti, Lisa Ditscherlein, Christina Schröder, Steffen Dudczig, Urs A. Peuker, Olena Volkova, Christos G. Aneziris, Horst Biermann, Anja Weidner, Nanoindentation of alumina and multiphase inclusions in 42CrMo4 steel, 2022.