Plot 2D velocity surfaces - phase, slowness & wavefront For given plane normal direction, for example xvector, yvector or zvector Stishovite (SiO2) at high pressure
David Mainprice 1/05/2018
The Elastic Stiffness Tensor of Stishovite
Reference: Elastic constants Stishovite, Weidner et al 1982 JGR Reference: Crystal Structure Sinclair and Ringwood 78 Nature P422 d=4.2901
% Define density (g/cm3)
rho= 4.2901;
% elastic Cij stiffness tensor (GPa) as matrix M
M = ...
[[ 453.00 211.00 203.00 0.00 0.00 0.00];...
[ 211.00 453.00 203.00 0.00 0.00 0.00];...
[ 203.00 203.00 776.00 0.00 0.00 0.00];...
[ 0.00 0.00 0.00 252.00 0.00 0.00];...
[ 0.00 0.00 0.00 0.00 252.00 0.00];...
[ 0.00 0.00 0.00 0.00 0.00 302.00]];
% define cartesian tensor crystal crystalSymmetry & frame
cs_Tensor = crystalSymmetry('4/mmm',[ 4.9133 4.9133 5.4048],...
[ 90.0000 90.0000 90.0000]*degree,'x||a','z||c',...
'mineral','Stishovite 1982');
%
% define elastic stiffness tensor Cijkl
C = stiffnessTensor(M,cs_Tensor,'density',rho);compute wave velocities and polarization directions
% the propagation direction is just the vector normal to the sphere
prop = S2AxisFieldHarmonic.normal;
% the wave velocities and polarization directions as directional dependend
% functions
[vp,vs1,vs2,pp,ps1,ps2] = velocity(C);Plotting settings
% plane normal direction for 2d sections
planeNormal = vector3d.Z;
% plotting convention - plot X-axis to east
plotx2east;
% close all open graphics
close all
% some global options for the titles
%titleOpt = {'FontSize',getMTEXpref('FontSize'),'visible','on','color','k'};
titleOpt = {'FontSize',25};
% option for legend
legendOpt = {'location','best'};
% option for mtexColorbar
ColorbarOpt = {'location','southoutside'};
% options for sections
optSec = {'color','interp','linewidth',5,'doNotDraw'};
% options for quiver
optQuiver = {'linewidth',5,'autoScaleFactor',0.25,'doNotDraw'};
% options for prop
optQuiverProp = {'color','k','linewidth',2,'autoScaleFactor',0.15,'doNotDraw'};1: Phase velocity surface (km/s)
figure(1)
% phase velocities
plotSection(vp,planeNormal,optSec{:})
hold on
plotSection(vs1,planeNormal,optSec{:})
plotSection(vs2,planeNormal,optSec{:})
% polarization directions
quiverSection(vp,pp,planeNormal,'color','c',optQuiver{:})
quiverSection(vs1,ps1,planeNormal,'color','g',optQuiver{:})
quiverSection(vs2,ps2,planeNormal,'color','m',optQuiver{:})
% plot propagation directions as reference
quiverSection(vp,prop,planeNormal,optQuiverProp{:})
quiverSection(vs1,prop,planeNormal,optQuiverProp{:})
quiverSection(vs2,prop,planeNormal,optQuiverProp{:})
axis off tight
legend('Vp','Vs1','Vs2','pp','ps1','ps2','X',legendOpt{:})
mtexTitle('Phase velocity surfaces (km/s)',titleOpt{:})
% seismic velocity slow = red 2 blue =fast
mtexColorMap red2blue
mtexColorbar('Title','(km/s)',ColorbarOpt{:})
% Az El for planeNormal = Z
%view(0,85)
hold off
drawNow(gcm,'figSize','large')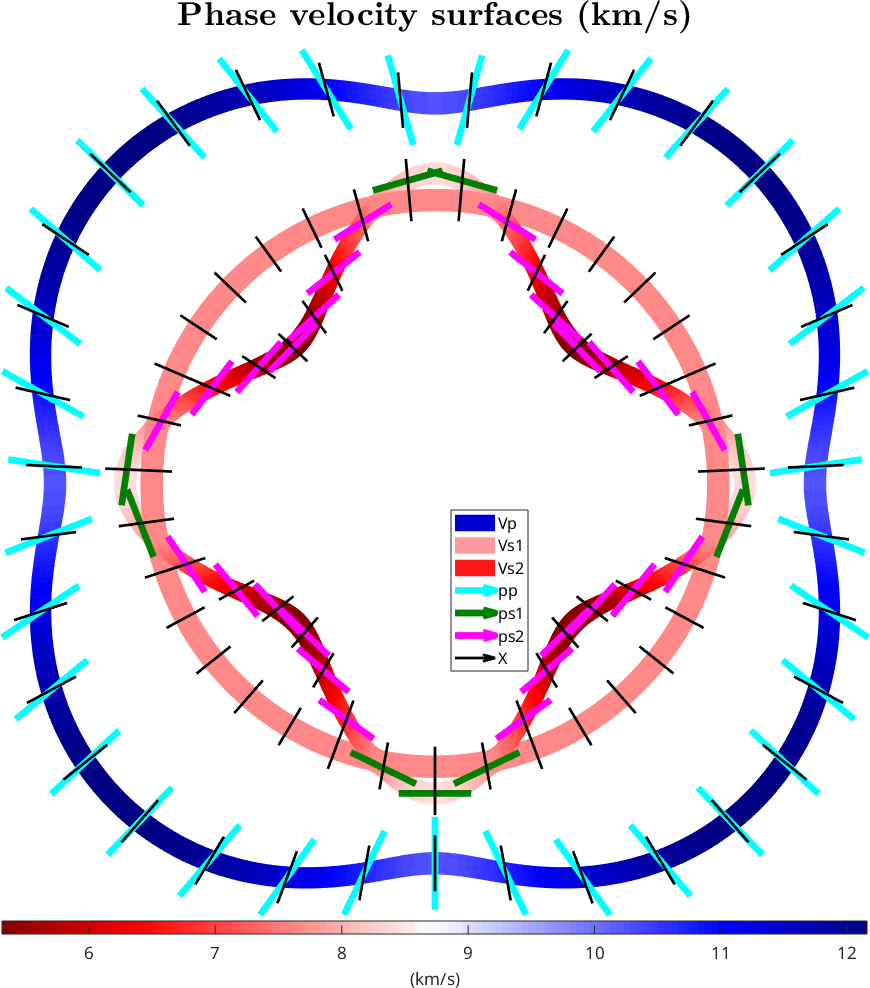
2: Slowness surface (s/km)
figure(2)
% slowness
plotSection(1./vp,planeNormal,optSec{:})
hold on
plotSection(1./vs1,planeNormal,optSec{:})
plotSection(1./vs2,planeNormal,optSec{:})
% polarization directions
quiverSection(1./vp,pp,planeNormal,'color','c',optQuiver{:})
quiverSection(1./vs1,ps1,planeNormal,'color','g',optQuiver{:})
quiverSection(1./vs2,ps2,planeNormal,'color','m',optQuiver{:})
% plot propagation directions as reference
quiverSection(1./vp,prop,planeNormal,optQuiverProp{:})
quiverSection(1./vs1,prop,planeNormal,optQuiverProp{:})
quiverSection(1./vs2,prop,planeNormal,optQuiverProp{:})
axis off tight
legend('Vp','Vs1','Vs2','pp','ps1','ps2','X',legendOpt{:})
mtexTitle('Slowness surfaces (km/s)',titleOpt{:})
% seismic slowness slow = blue 2 red =fast
mtexColorMap blue2red
mtexColorbar('Title','(s/km)',ColorbarOpt{:})
% Az El for planeNormal = Z
%view(0,85)
hold off
drawNow(gcm,'figSize','large')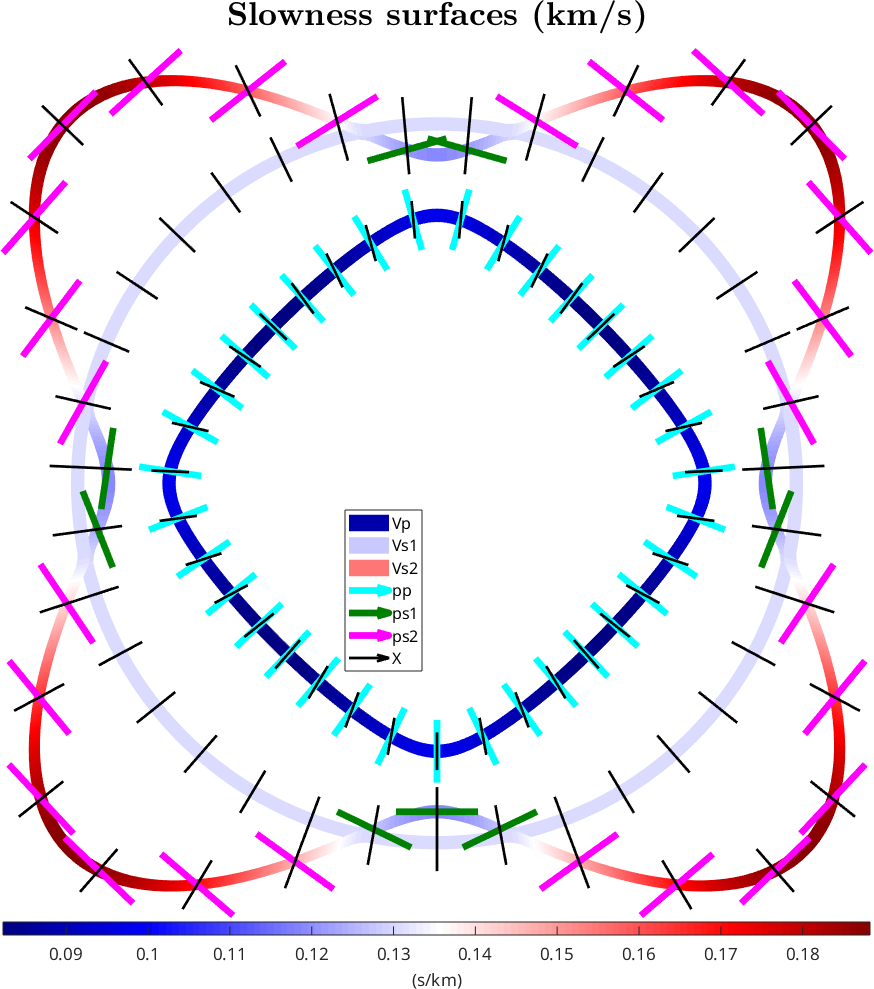
Select the two S-waves (Vs1 and Vs2 where Vs1>Vs2 in velocity)
by the orientation of the polarization vectors ps1 and ps2 with respect to the specimen Z direction. So that sv (v=vertical) is S-wave with polarization closest to Z sh (h=horizontal) has the polarization closest to the plane normal to Z Both polarizations pairs (sv and sh) and (ps1 and ps2) are orthogonal
which values to switch this defines a function which is either one or zero
id = angle(ps1,vector3d.Z) <= 89.9*degree;
vsv = id .* vs1 + (1-id) .* vs2;
vsh = id .* vs2 + (1-id) .* vs1;
psv = id .* ps1 + (1-id) .* ps2;
psh = id .* ps2 + (1-id) .* ps1;1: Phase velocity surface (km/s) with sv1 & vs2
figure(1)
% phase velocities
plotSection(vp,planeNormal,optSec{:})
hold on
plotSection(vs1,planeNormal,optSec{:})
plotSection(vs2,planeNormal,optSec{:})
% polarization directions
quiverSection(vp,pp,planeNormal,'color','c',optQuiver{:})
quiverSection(vs1,ps1,planeNormal,'color','g',optQuiver{:})
quiverSection(vs2,ps2,planeNormal,'color','m',optQuiver{:})
% plot propagation directions as reference
quiverSection(vp,prop,planeNormal,optQuiverProp{:})
quiverSection(vs1,prop,planeNormal,optQuiverProp{:})
quiverSection(vs2,prop,planeNormal,optQuiverProp{:})
axis off tight
legend('Vp','Vs1','Vs2','pp','ps1','ps2','X',legendOpt{:})
mtexTitle('Phase velocity surfaces (km/s)',titleOpt{:})
mtexColorMap blue2red
mtexColorbar('Title','(km/s)',ColorbarOpt{:})
% Az El for planeNormal = Z
%view(0,85)
hold off
drawNow(gcm,'figSize','large')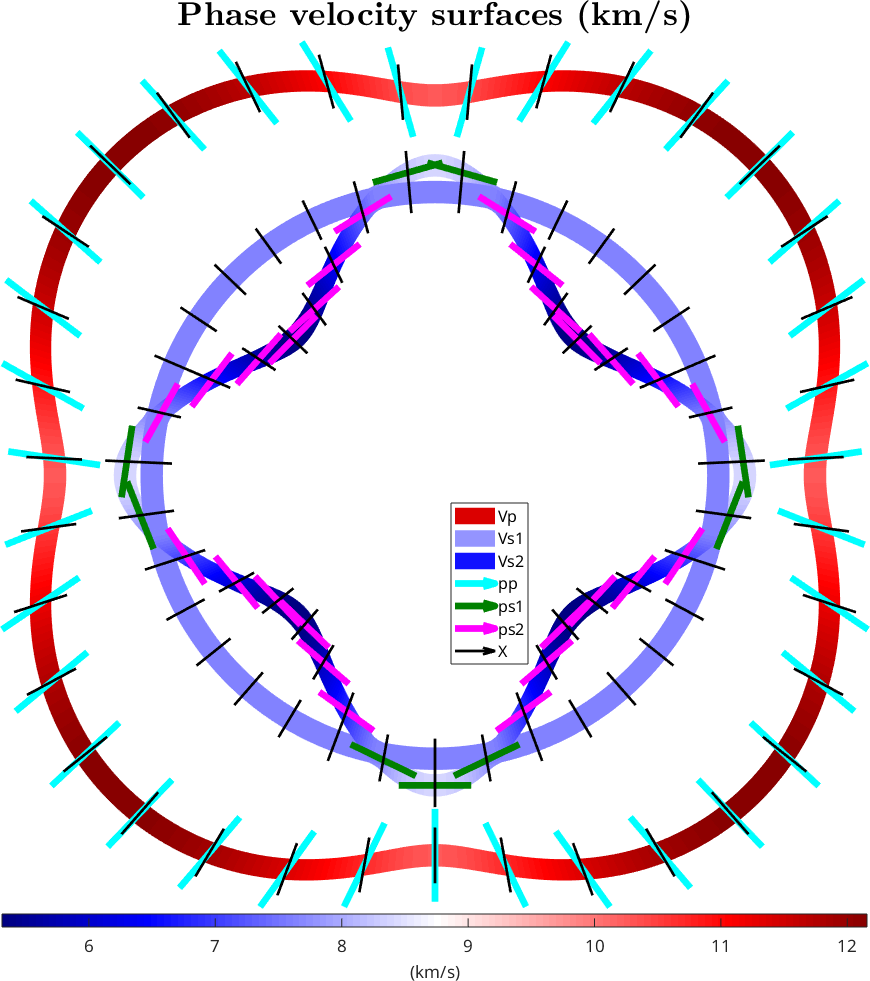
2: Phase velocity surface (km/s) with svs & vsh
figure(2)
% phase velocities
plotSection(vp,planeNormal,optSec{:})
hold on
plotSection(vsv,planeNormal,optSec{:})
plotSection(vsh,planeNormal,optSec{:})
% polarization directions
quiverSection(vp,pp,planeNormal,'color','c',optQuiver{:})
quiverSection(vsv,ps1,planeNormal,'color','g',optQuiver{:})
quiverSection(vsh,ps2,planeNormal,'color','m',optQuiver{:})
% plot propagation directions as reference
quiverSection(vp,prop,planeNormal,optQuiverProp{:})
quiverSection(vsv,prop,planeNormal,optQuiverProp{:})
quiverSection(vsh,prop,planeNormal,optQuiverProp{:})
axis off tight
legend('Vp','Vsv','Vsh','pp','ps1','ps2','X',legendOpt{:})
mtexTitle('Phase velocity surfaces (km/s)',titleOpt{:})
mtexColorMap blue2red
mtexColorbar('Title','(km/s)',ColorbarOpt{:})
% Az El for planeNormal = Z
%view(0,85)
hold off
drawNow(gcm,'figSize','large')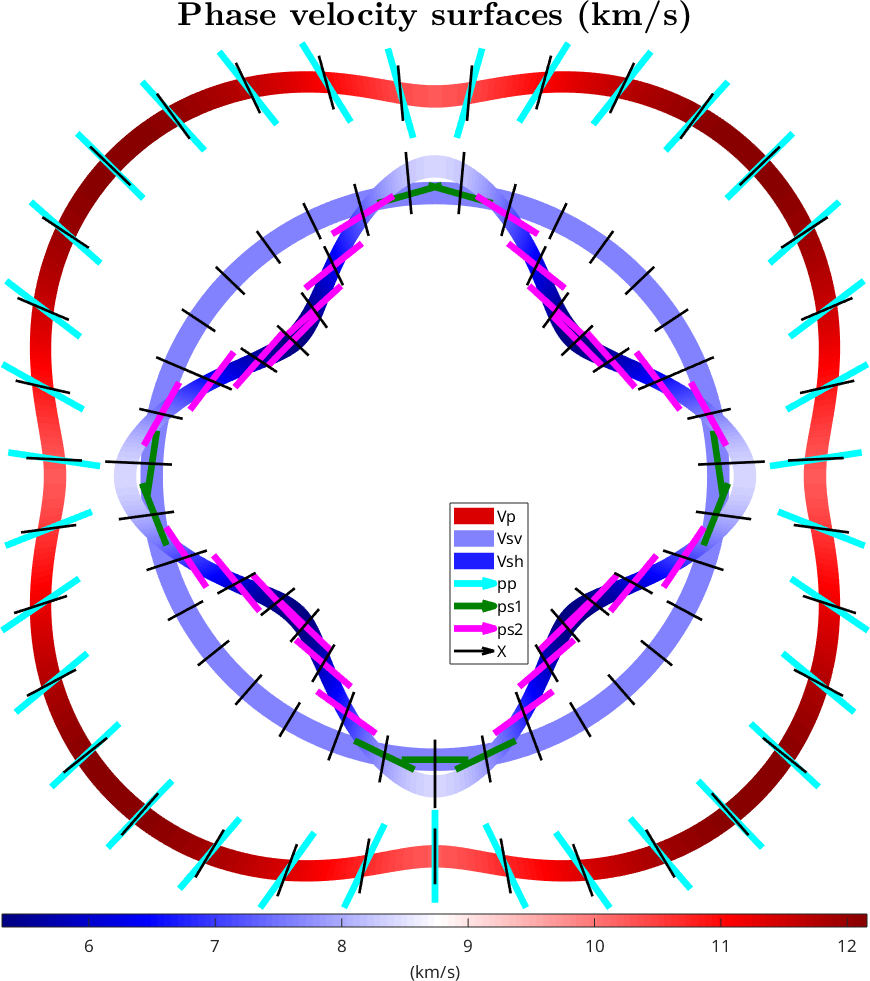
3: plot slowness in plane normal Z
figure(3)
plotSection(1./vp,planeNormal,optSec{:})
hold on
plotSection(1./vs1,planeNormal,optSec{:})
plotSection(1./vs2,planeNormal,optSec{:})
% polarization vectors pp,ps1,ps2
quiverSection(1./vp,pp,planeNormal,'color','c',optQuiver{:})
quiverSection(1./vs1,ps1,planeNormal,'color','g',optQuiver{:})
quiverSection(1./vs2,ps2,planeNormal,'color','m',optQuiver{:})
% propagation vectors (prop)
quiverSection(1./vp,prop,planeNormal,optQuiverProp{:})
quiverSection(1./vs1,prop,planeNormal,optQuiverProp{:})
quiverSection(1./vs2,prop,planeNormal,optQuiverProp{:})
axis off tight
legend('Sp','Ss1','Ss2','Sp','Ss1','Ss2','X',legendOpt{:})
mtexTitle('Stishovite : Slowness surfaces (s/km)',titleOpt{:})
% seismic slowness slow = blue 2 red =fast
mtexColorMap red2blue
mtexColorbar('Title','(s/km)',ColorbarOpt{:})
hold off
drawNow(gcm,'figSize','large')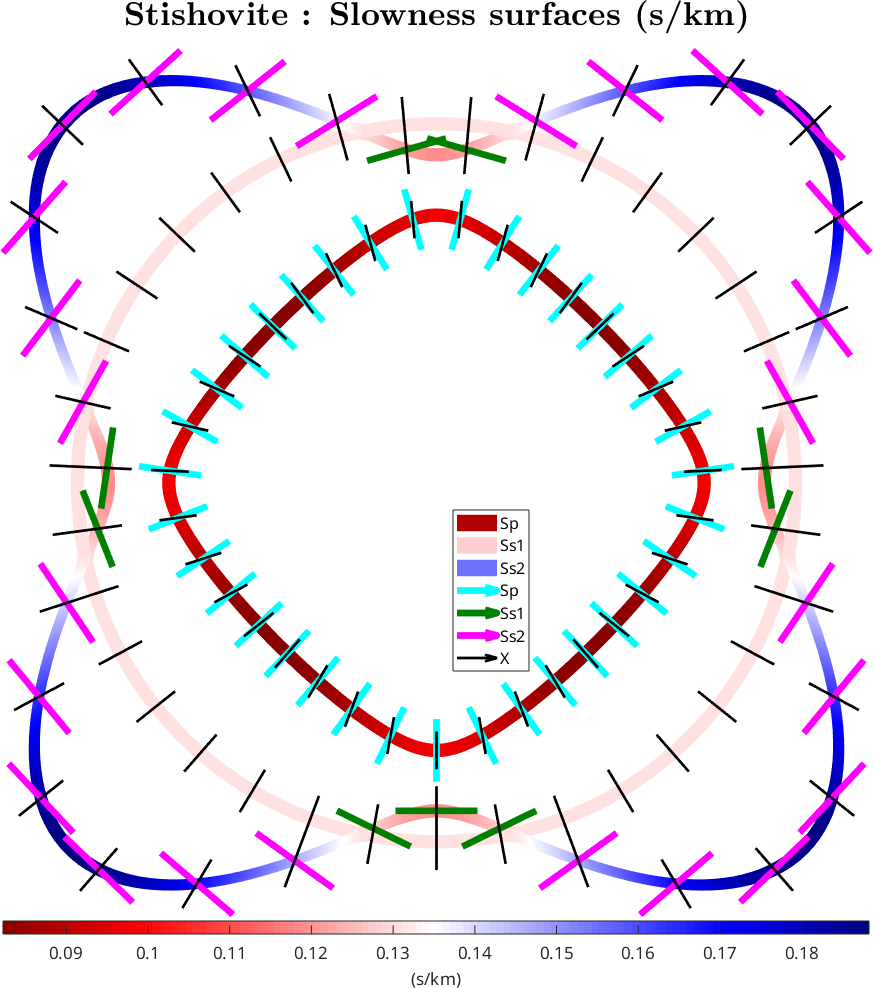
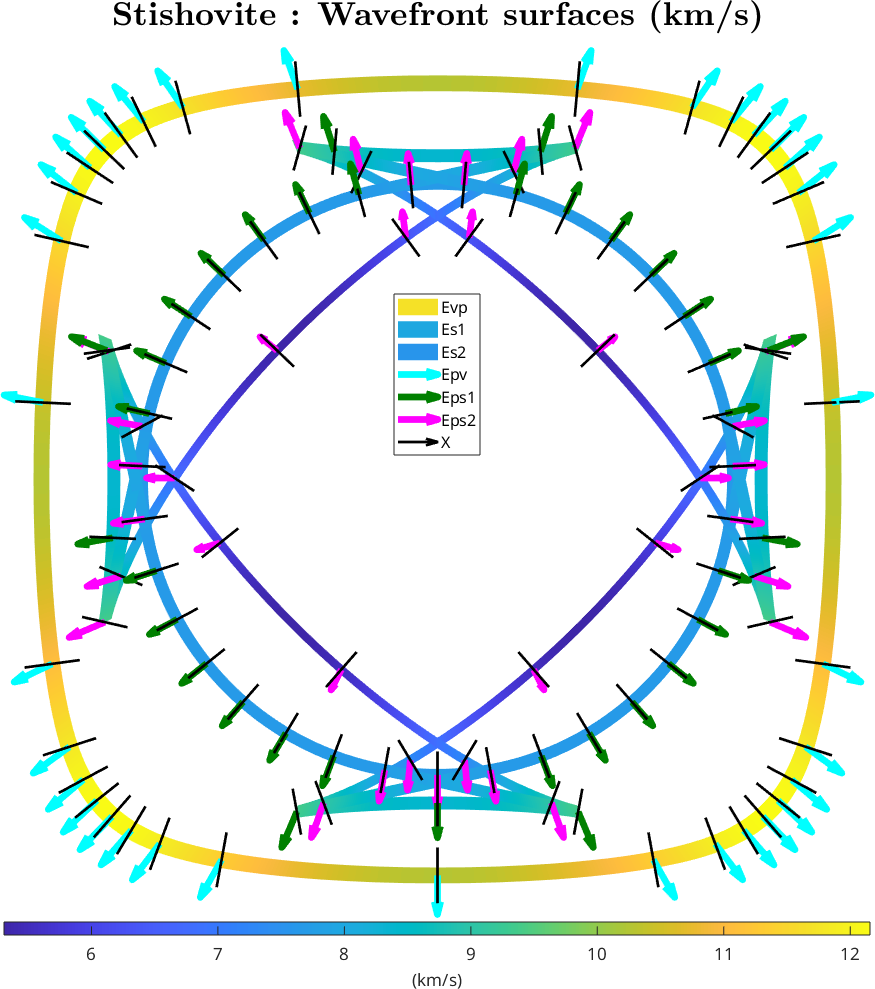
Compute WaveFront as spherical functions: EnergyVectors Evp, Evs1 & Evs2
Evp = energyVector(C,[],vp,pp);
Evs1 = energyVector(C,[],vs1,ps1);
Evs2 = energyVector(C,[],vs2,ps2);plot wavefront in plane normal Z
close all
% Vp,Vs1,Vs2 wavefronts with motif
%optSec = {'linewidth',5,'doNotDraw'};
optSec = {'color','interp','linewidth',2,'doNotDraw'};
plotSection(Evp,planeNormal,optSec{:})
hold on
plotSection(Evs1,planeNormal,optSec{:})
plotSection(Evs2,planeNormal,optSec{:})
%
% polarization vectors pp,ps1,ps2
quiverSection(Evp,Evp,planeNormal,'color','c',optQuiver{:})
quiverSection(Evs1,Evs1,planeNormal,'color','g',optQuiver{:})
quiverSection(Evs2,Evs2,planeNormal,'color','m',optQuiver{:})
% propagation vectors (prop)
quiverSection(Evp,prop,planeNormal,optQuiverProp{:})
quiverSection(Evs1,prop,planeNormal,optQuiverProp{:})
quiverSection(Evs2,prop,planeNormal,optQuiverProp{:})
axis off tight
legend('Evp','Es1','Es2','Epv','Eps1','Eps2','X',legendOpt{:})
mtexTitle('Stishovite : Wavefront surfaces (km/s)',titleOpt{:})
mtexColorbar('Title','(km/s)',ColorbarOpt{:})
hold off
drawNow(gcm,'figSize','large')
% End of demo