Pole Figure Data (The Class PoleFigure)
This section describes the class PoleFigure and gives an overview of the functionality MTEX offers to analyze pole figure data.
| On this page ... |
| Class Description |
| Import pole figure data |
| Plot pole figure data |
| Manipulate pole figure data |
| Calculate an ODF from pole figure data |
| Simulate pole figure data |
| Complete Function list |
Class Description
The general workflow to deal with pole figure data in MTEX is as follows.
- Import the pole figure data and create a variable of type PoleFigure
- Visualize the pole figure data
- Manipulate the pole figure data
- Compute an ODF from the pole figure data
Import pole figure data
The most comfortable way to import pole figure data into MTEX is to use the import wizard, which can be started by the command
import_wizard
If the data are in a format supported by MTEX the import wizard generates a script which imports the data. More information about the import wizard and a list of supported file formats can be found here. A typical script generated by the import wizard looks as follows.
% specify scrystal and specimen symmetry cs = crystalSymmetry('-3m',[1.4,1.4,1.5]); % specify file names fname = {... fullfile(mtexDataPath,'PoleFigure','dubna','Q(10-10)_amp.cnv'),... fullfile(mtexDataPath,'PoleFigure','dubna','Q(10-11)(01-11)_amp.cnv'),... fullfile(mtexDataPath,'PoleFigure','dubna','Q(11-22)_amp.cnv')}; % specify crystal directions h = {Miller(1,0,-1,0,cs),[Miller(0,1,-1,1,cs),Miller(1,0,-1,1,cs)],Miller(1,1,-2,2,cs)}; % specify structure coefficients c = {1,[0.52 ,1.23],1}; % import pole figure data pf = PoleFigure.load(fname,h,cs,'superposition',c) % After running the script the variable *pf* is created which contains all % information about the pole figure data.
pf = PoleFigure crystal symmetry : -3m1, X||a*, Y||b, Z||c* specimen symmetry: 1 h = (10-10), r = 72 x 19 points h = (01-11)(10-11), r = 72 x 19 points h = (11-22), r = 72 x 19 points
Plot pole figure data
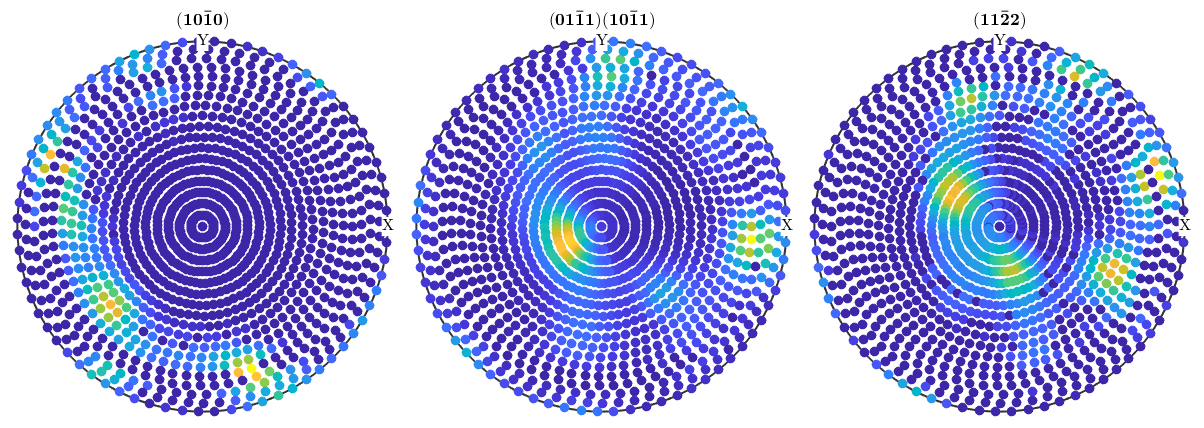
Pole figures are plotted using the plot command. It plottes a single colored dot for any data point contained in the pole figure. There are many options to specify the way pole figures are plotted in MTEX. Have a look at the plotting section for more information.
figure plot(pf)
Manipulate pole figure data
MTEX offers a large collection of operations to analyze and manipulate pole figure data, e.g.
- rotate pole figures
- scale pole figures
- find outliers
- remove specific measurements
- superpose pole figures
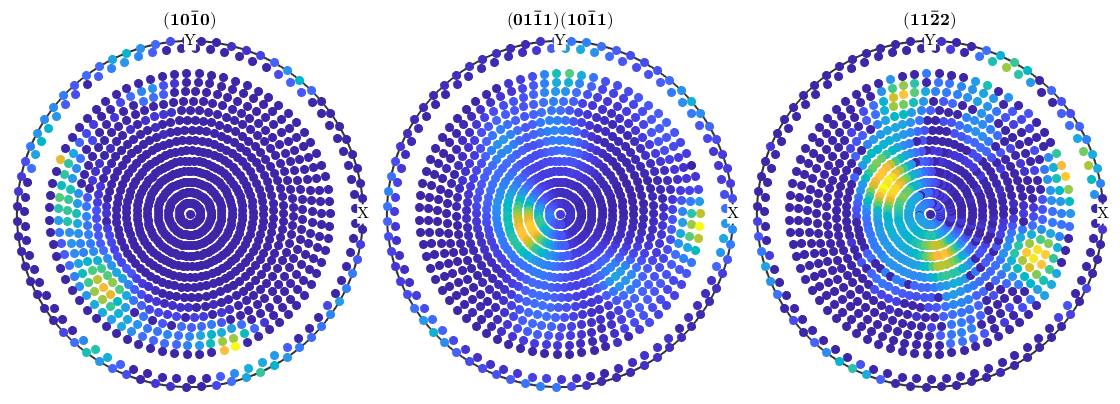
An exhaustive introduction how to modify pole figure data can be found here As an example, if one wants to remove all intensities with polar angle between 74 and 81 degree one can do
pf(pf.r.theta >= 74*degree & pf.r.theta <= 81*degree) = []; plot(pf)
Calculate an ODF from pole figure data
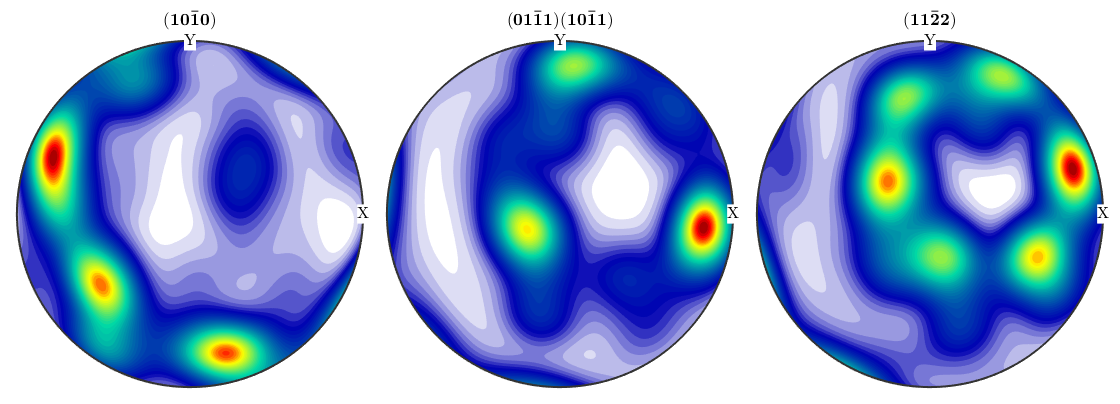
Calculating an ODF from pole figure data can be done using the command calcODF. A precise description of the underlying algorithm as well as of the options can be found here
odf = calcODF(pf,'zero_range','silent') plotPDF(odf,h,'superposition',c,'antipodal')
odf = ODF
crystal symmetry : -3m1, X||a*, Y||b, Z||c*
specimen symmetry: 1
Radially symmetric portion:
kernel: de la Vallee Poussin, halfwidth 10°
center: 19811 orientations, resolution: 5°
weight: 1
Simulate pole figure data
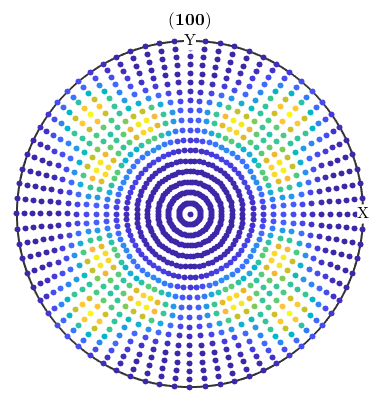
Simulating pole figure data from a given ODF has been proven to be useful to analyze the stability of the ODF estimation process. There is an example demonstrating how to determine the number of pole figures to estimate the ODF up to a given error. The MTEX command to simulate pole figure is calcPoleFigure, e.g.
cs = crystalSymmetry('m-3m')
pf = calcPoleFigure(SantaFe,Miller(1,0,0,cs),regularS2Grid)
plot(pf)cs = crystalSymmetry symmetry: m-3m a, b, c : 1, 1, 1 pf = PoleFigure crystal symmetry : m-3m specimen symmetry: 222 h = (100), r = 72 x 37 points
Complete Function list
| *PoleFigure* is the low level constructor. For importing real world data | |
| interfaces.html"> you might want to use the predefined interfaces | |
| Input | |
| h | crystal directions (@vector3d | @Miller) |
| r | specimen directions (@S2Grid) |
| intensities | diffraction counts (double) |
| CS,SS | crystal, specimen @symmetry |
| Options | |
| superposition | weights for superposed crystal directions |
| background | background intensities |
| See also | |
| ImportPoleFigureData loadPoleFigure loadPoleFigure_generic |
| DocHelp 0.1 beta |