Crystal Orientations (The Class orientation)
This sections describes the class orientation and gives an overview how to work with crystal orientation in MTEX.
Class Description
In texture analysis crystal orientations are used to describe the alignment of the crystals within the specimen. A crystal orientation is defined as the rotation that maps the specimen coordinate system onto the crystal coordinate system. Since the crystal coordinate system and the specimen coordinate system are well defined only up to crystal symmetry and specimen symmetry, an orientation is in general represented by a class of crystallographically equivalent rotations. In MTEX the class orientation is an inheritance of the class rotation. In particular, every function that is defined for a rotation is also available for an orientation.
Defining a Crystal Orientation
In order to define a crystal orientation one has to define crystal and specimen symmetry first.
cs = crystalSymmetry('cubic'); ss = specimenSymmetry('orthorhombic');
Now a crystal orientation to a certain rotation
rot = rotation.byEuler(30*degree,50*degree,10*degree);
is defined by
o = orientation(rot,cs,ss)
o = orientation
size: 1 x 1
crystal symmetry : m-3m
specimen symmetry: mmm
Bunge Euler angles in degree
phi1 Phi phi2 Inv.
30 50 10 0
In order to streamline the definition the arguments to define the rotation can be directly pass to define a orientation:
o = orientation.byEuler(30*degree,50*degree,10*degree,cs,ss)
o = orientation
size: 1 x 1
crystal symmetry : m-3m
specimen symmetry: mmm
Bunge Euler angles in degree
phi1 Phi phi2 Inv.
30 50 10 0
Accordingly parameterisations of rotations are also available for orientations
- Bunge Euler Angle Convention
- Matthies Euler Angle Convention
- Axis angle parametrisation
- Fibre of orientations
- Four vectors defining a rotation
- 3 times 3 matrix
- quaternion
Have a look at rotation help page for more details. Besides these parameterisations for rotations there are also some parameterisations which are unique for orientations
Miller indices
There is also a Miller indices convention for defining crystal orientations.
o = orientation.byMiller([1 0 0],[0 1 1],cs,ss)
o = orientation size: 1 x 1 crystal symmetry : m-3m specimen symmetry: mmm Bunge Euler angles in degree phi1 Phi phi2 Inv. 135 90 90 0
Predifined Orientations
In the MTEX there is a list of predefined orientations:
o = orientation.goss(cs,ss)
o = orientation
size: 1 x 1
crystal symmetry : m-3m
specimen symmetry: mmm
Bunge Euler angles in degree
phi1 Phi phi2 Inv.
0 45 0 0
Rotating Crystal Directions onto Specimen Directions
Let
h = Miller(1,0,0,cs)
h = Miller size: 1 x 1 symmetry: m-3m h 1 k 0 l 0
be a certain crystal direction and
o = orientation.byEuler(90*degree,90*degree,0*degree,cs,ss)
o = orientation
size: 1 x 1
crystal symmetry : m-3m
specimen symmetry: mmm
Bunge Euler angles in degree
phi1 Phi phi2 Inv.
90 90 0 0
a crystal orientation. Then the alignment of this crystal direction with respect to the specimen coordinate system can be computed via
r = o * h
r = vector3d size: 1 x 1 x y z 0 1 0
Conversely the crystal direction that is mapped onto a certain specimen direction can be computed via the backslash operator
o \ r
ans = Miller size: 1 x 1 symmetry: m-3m h 1 k 0 l 0
Concatenating Rotations
Let
o = orientation.byEuler(90*degree,0,0,cs,ss); rot = rotation.byEuler(0,60*degree,0);
be a crystal orientation and a rotation of the specimen coordinate system. Then the orientation of the crystal with respect to the rotated specimen coordinate system calculates by
o1 = rot * o
o1 = orientation
size: 1 x 1
crystal symmetry : m-3m
specimen symmetry: 1
Bunge Euler angles in degree
phi1 Phi phi2 Inv.
0 60 90 0
Then the class of rotations crystallographically equivalent to o can be computed in two ways. Either by using the command symmetrise
symmetrise(o)
ans = orientation size: 384 x 1 crystal symmetry : m-3m specimen symmetry: mmm
or by using multiplication
ss * o * cs
ans = orientation size: 8 x 48 crystal symmetry : m-3m specimen symmetry: mmm
Calculating Misorientations
Let cs and ss be crystal and specimen symmetry and o1 and o2 two crystal orientations. Then one can ask for the misorientation between both orientations. This misorientation can be calculated by the function angle.
angle(rot * o1,o1) / degree
ans = 30.0000
This misorientation angle is, in general, smaller than the misorientation without crystal symmetry which can be computed via
angle(rotation(o),rotation(o1)) /degree
ans = 60.0000
Calculating with Orientations and Rotations
Besides the standard linear algebra operations there are also the following functions available in MTEX. Then rotational angle and the axis of rotation can be computed via then commands angle(o) and axis(o)
angle(o1)/degree axis(o1)
ans = 30.0000 ans = Miller size: 1 x 1 symmetry: 1, X||a, Y||b*, Z||c* h -1 k 0 l 0
The inverse orientation to o you get from the command inv(q)
inv(o1)
ans = inverse orientation
size: 1 x 1
specimen symmetry: 1
crystal symmetry : m-3m
Bunge Euler angles in degree
phi1 Phi phi2 Inv.
90 60 180 0
Conversion into Euler Angles and Rodrigues Parametrisation
There are methods to transform quaternion in almost any other parameterization of rotations as they are:
- Euler(o) in Euler angle
- Rodrigues(o) % in Rodrigues parameter
[phi1,Phi,phi2] = Euler(o)
phi1 =
1.5708
Phi =
0
phi2 =
0
Plotting Orientations
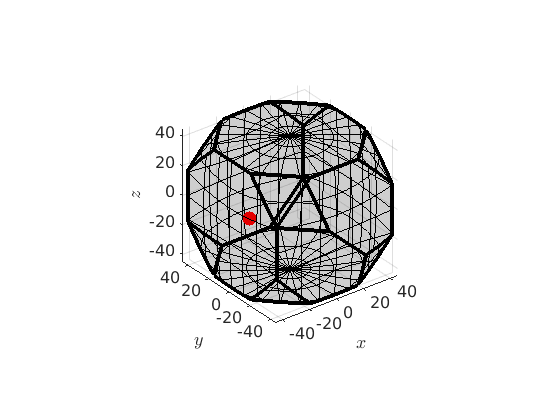
The plot function allows you to visualize an orientation in axis angle space in relation to its fundamental region.
oR = fundamentalRegion(o1.CS,o1.SS) plot(oR) hold on % plot the orientation as it is plot(o1,'markercolor','b','markerSize',10) % plot the orientation within the fundamental zone plot(o1.project2FundamentalRegion,'markercolor','r','markerSize',10) hold off
oR = orientationRegion crystal symmetry: 432 max angle: 62.7994° face normales: 14 vertices: 24
Complete Function list
| DocHelp 0.1 beta |