Crystal and Specimen Symmetries (The Class symmetry)

This section describes the class symmetry and gives an overview how to deal with crystal symmetries in MTEX.

Class Description

Crystal symmetries are sets of rotations and mirroring operations that leave the lattice of a crystal invariant. They form so-called groups since the concatenation of two symmetry operations is again a symmetry operation. Crystal symmetries are classified in various ways - either according to the corresponding space group or the corresponding point group, or the corresponding Laue group. In total, there are only 11 different Laue groups present in crystallography. All these 11 Laue groups are supported by MTEX. More precisely, in MTEX a Laue group is represented by a variable of the class symmetry.

Defining a Crystal Symmetry

MTEX supports the Schoenflies notation on Laue groups as well as the international notation. In the case of noncubic crystal symmetry the length of the crystal axis has to be specified as a second argument to the constructor symmtry and in the case of triclinic crystal symmetry the angles between the axes has to be passed as the third argument. Hence, valid definitions are:

Laue Group - international notation

cs = crystalSymmetry('m-3m')

 
cs = crystalSymmetry  
 
  symmetry: m-3m   
  a, b, c : 1, 1, 1

Laue Group - Schoenflies notation

cs = crystalSymmetry('O')

 
cs = crystalSymmetry  
 
  symmetry: 432    
  a, b, c : 1, 1, 1

Point Group or its Space Group

If not the name of a Laue group was specified but the name of a point group or a space group MTEX automatically determines the corresponding Laue group and assigns it to the variable.

cs = crystalSymmetry('Td')

 
cs = crystalSymmetry  
 
  symmetry: -43m   
  a, b, c : 1, 1, 1

CIF Files

Finally, MTEX allows defining a crystal symmetry by importing a crystallographic information file (*.cif).

cs = loadCIF('quartz')

 
cs = crystalSymmetry  
 
  mineral        : Quartz            
  symmetry       : 321               
  a, b, c        : 4.9, 4.9, 5.4     
  reference frame: X||a*, Y||b, Z||c*

The Crystal Coordinate System

In the case of cubic crystal symmetry the crystal coordinate system is already well defined. However, especially in the case of low order crystal symmetry, the crystal coordinate system has to be specified by the length of the axis and the angle between the axis.

cs = crystalSymmetry('triclinic',[1,2.2,3.1],[80*degree,85*degree,95*degree]);

A and B Configurations

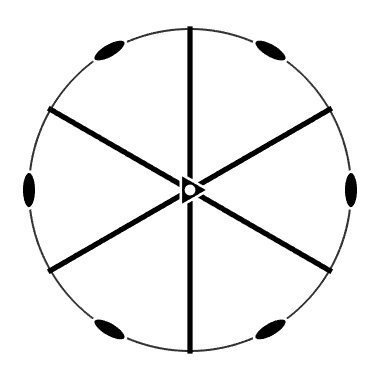
In the case of trigonal and hexagonal crystal symmetries different conventions are used. One distinguishes between the A and the B configuration depending whether the a-axis is aligned parallel to the x-axis or parallel to the y-axis. In order to specify the concrete

cs = crystalSymmetry('-3m',[1.7,1.7,1.4],'X||a');
plot(cs)

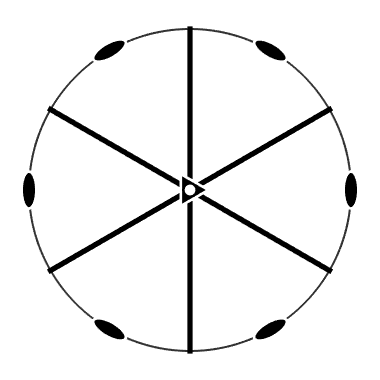
cs = crystalSymmetry('-3m',[1.7,1.7,1.4],'Y||a');
plot(cs)

Complete Function list

`Supported Symmetries`

`id crystal system Schoen`	Inter Laue Rotational
`flies national class axes`
`1 triclinic C1 1`	1
`2 triclinic Ci`	1 1
`3 monoclinic C2 2 2/m 2`
`4 monoclinic Cs m 2/m 2`
`5 monoclinic C2h 2/m 2/m 2`
`6 orthorhombic D2 222 mmm 222`
`7 orthorhombic C2v mm2 mmm 222`
`8 orthorhombic D2h mmm mmm 222`
`9 tetragonal C4 4 4/m 4`
`10 tetragonal S4`	4/m 4
`11 tetragonal C4h 4/m 4/m 4`
`12 tetragonal D4 422 4/mmm 422`
`13 tetragonal C4v 4mm 4/mmm 422`
`14 tetragonal D2d`	2m 4/mmm 422
`15 tetragonal D4h 4/mmm 4/mmm 422`
`16 trigonal C3 3`	3
`17 trigonal C3i`	3 3
`18 trigonal D3 32`	m 32
`19 trigonal C3v 3m`	m 32
`20 trigonal D3d`	m 3m 32
`21 hexagonal C6 6 6/m 6`
`22 hexagonal C3h`	6/m 6
`23 hexagonal C6h 6/m 6/m 6`
`24 hexagonal D6 622 6/mmm 622`
`25 hexagonal C6v 6mm 6/mmm 622`
`26 hexagonal D3h`	m2 6/mmm 622
`27 hexagonal D6h 6/mmm 6/mmm 622`
`28 cubic T 23 m`	23
`29 cubic Th m`	m3 23
`30 cubic O 432 m`	m 432
`31 cubic Td`	3m m3m 432
`32 cubic Oh m`	m m3m 432