ODF Shapes (The class kernel)
standard distributions on SO(3)
| On this page ... |
| Class Description |
| Defining a kernel function |
| Plotting the kernel |
| Complete Function list |
Class Description
The class kernel is needed in MTEX to define the specific form of unimodal and fibre symmetric ODFs. It has to be passed as an argument when calling the methods uniformODF and fibreODF.
Defining a kernel function
A kernel is defined by specifying its name and its free parameter. Alternatively one can also specify the halfwidth of the kernel. Below you find a list of all kernel functions supported by MTEX.
psi{1} = AbelPoissonKernel(0.79);
psi{2} = deLaValleePoussinKernel(13);
psi{3} = vonMisesFisherKernel(7.5);
psi{4} = bumpKernel(35*degree);
psi{5} = DirichletKernel(3);
psi{6} = GaussWeierstrassKernel(0.07);
psi{7} = fibreVonMisesFisherKernel(7.2);
psi{8} = SquareSingularityKernel(0.72);
Plotting the kernel
Using the plot command you can plot the kernel as a function on SO(3) as well as the corresponding PDF, or its Fourier coefficients
% the kernel on SO(3) close; figure('position',[100,100,700,450]) hold all for i = 1:numel(psi) plot(psi{i},'DisplayName',class(psi{i})); end hold off legend(gca,'show')

the corresponding PDF
close; figure('position',[100,100,700,450]) hold all for i = 1:numel(psi) plotPDF(psi{i},'RK','DisplayName',class(psi{i})); end hold off ylim([-1,20]) legend(gca,'show')
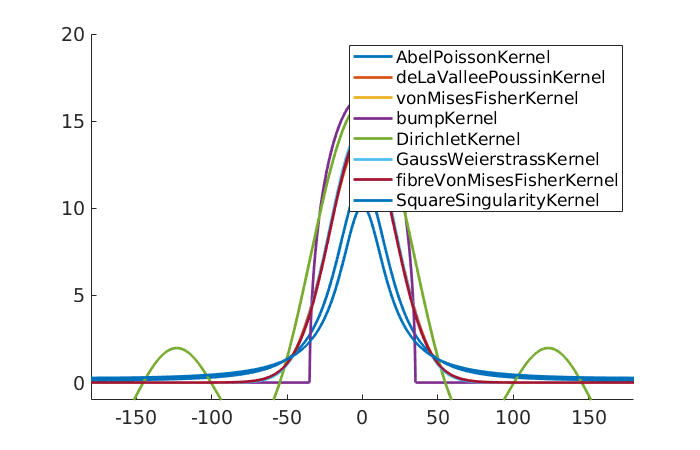
the Fourier coefficients of the kernels
close; figure('position',[100,100,500,450]) hold all for i = 1:numel(psi) plotFourier(psi{i},'bandwidth',32,'DisplayName',class(psi{i})); end hold off legend(gca,'show')

Complete Function list
| psi = kernel(A) |
| DocHelp 0.1 beta |