Ghost Effect Analysis

Introduction

A general problem in estimating an ODF from pole figure data is the fact that the odd order Fourier coefficients of the ODF are not present anymore in the pole figure data and therefore it is difficult to estimate them. Artifacts in the estimated ODF that are due to underestimated odd order Fourier coefficients are called ghost effects. It is known that for sharp textures the ghost effect is relatively small due to the strict non-negativity condition. For weak textures, however, the ghost effect might be remarkable. For those cases, MTEX provides the option ghost_correction which tries to determine the uniform portion of the unknown ODF and to transform the unknown weak ODF into a sharp ODF by substracting this uniform portion. This is almost the approach Matthies proposed in his book (He called the uniform portion phon). In this section, we are going to demonstrate the power of ghost correction at a simple, synthetic example.

Back to Top

Construct Model ODF

A unimodal ODF with a high uniform portion.

cs = crystalSymmetry('222');
mod1 = orientation.byEuler(0,0,0,cs);
odf = 0.9*uniformODF(cs) + ...
  0.1*unimodalODF(mod1,'halfwidth',10*degree)

 
odf = ODF  
  crystal symmetry : 222
  specimen symmetry: 1
 
  Uniform portion:
    weight: 0.9
 
  Radially symmetric portion:
    kernel: de la Vallee Poussin, halfwidth 10°
    center: (0°,0°,0°)
    weight: 0.1
 

Back to Top

Simulate pole figures

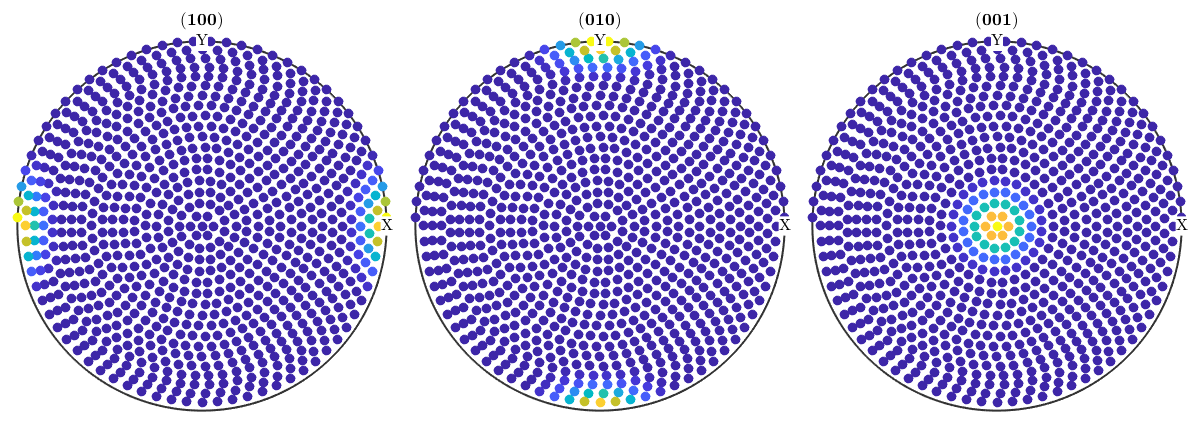
% specimen directions
r = equispacedS2Grid('resolution',5*degree,'antipodal');

% crystal directions
h = [Miller(1,0,0,cs),Miller(0,1,0,cs),Miller(0,0,1,cs)];

% compute pole figures
pf = calcPoleFigure(odf,h,r);

plot(pf)

Back to Top

ODF Estimation

without ghost correction:

rec = calcODF(pf,'noGhostCorrection','silent');

with ghost correction:

rec_cor = calcODF(pf,'silent');

Back to Top

Compare RP Errors

without ghost correction:

calcError(pf,rec,'RP')

progress: 100%
ans =
    0.1617    0.1600    0.1685

with ghost correction:

calcError(pf,rec_cor,'RP')

progress: 100%
ans =
    0.1547    0.1519    0.1584

Back to Top

Compare Reconstruction Errors

without ghost correction:

calcError(rec,odf)

progress: 100%
ans =
    0.1142

with ghost correction:

calcError(rec_cor,odf)

progress: 100%
ans =
    0.0269

Back to Top

Plot the ODFs

without ghost correction:

plot(rec,'sections',9,'silent','sigma')

progress: 100%

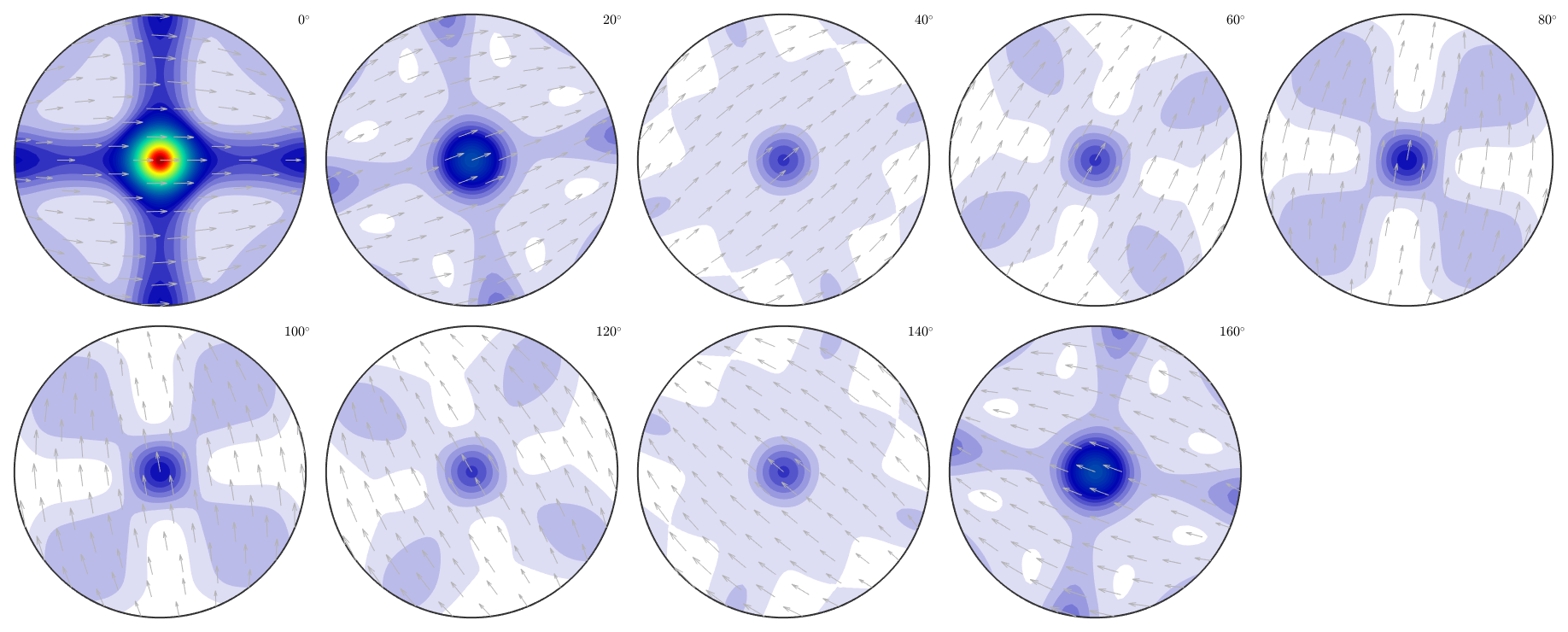
with ghost correction:

plot(rec_cor,'sections',9,'silent','sigma')

progress: 100%

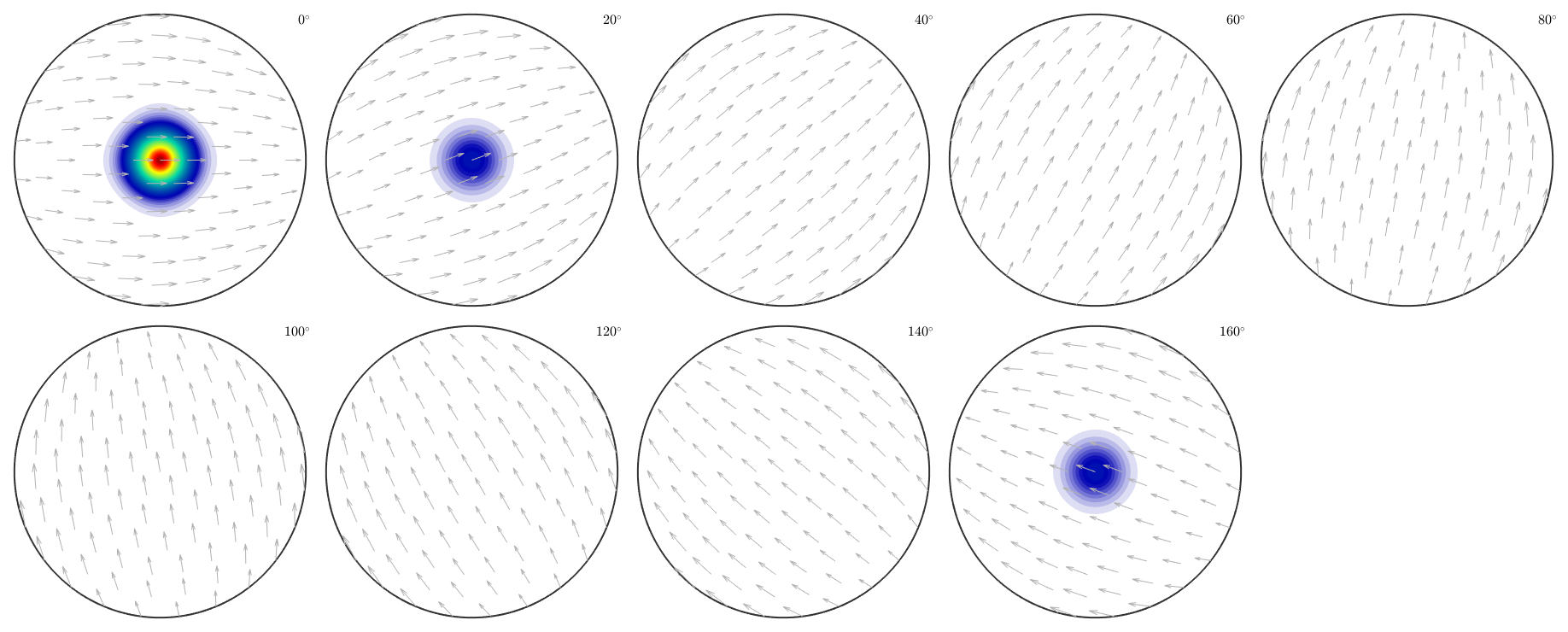
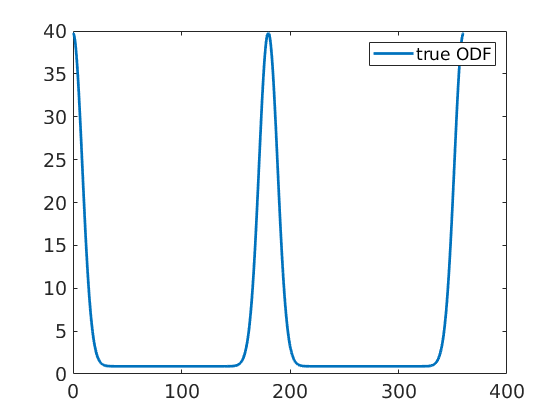
radial plot of the true ODF

close all
f = fibre(Miller(0,1,0,cs),yvector);
plot(odf,f,'linewidth',2);
hold all

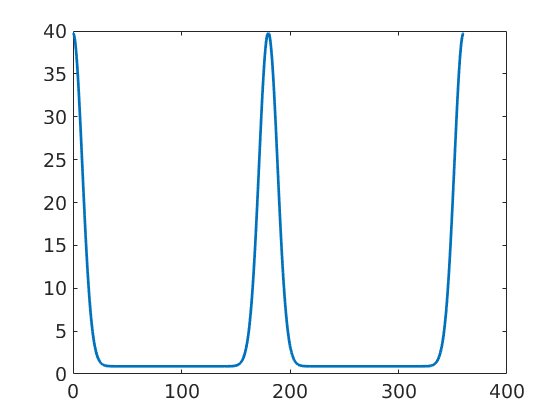
radial plot without ghost correction:

plot(rec,f,'linewidth',2);

radial plot with ghost correction:

plot(rec_cor,f,'linestyle','--','linewidth',2);
hold off
legend({'true ODF','without ghost correction','with ghost correction'})

Back to Top

Calculate Fourier coefficients

Next, we want to analyze the fit of the Fourier coefficients of the reconstructed ODFs. To this end, we first compute Fourier representations for each ODF

odf = FourierODF(odf,25)
rec = FourierODF(rec,25)
rec_cor = FourierODF(rec_cor,25)

 
odf = ODF  
  crystal symmetry : 222
  specimen symmetry: 1
 
  Harmonic portion:
    degree: 25
    weight: 1
 
 
rec = ODF  
  crystal symmetry : 222
  specimen symmetry: 1
 
  Harmonic portion:
    degree: 25
    weight: 1
 
 
rec_cor = ODF  
  crystal symmetry : 222
  specimen symmetry: 1
 
  Harmonic portion:
    degree: 25
    weight: 1
 

Back to Top

Calculate Reconstruction Errors from Fourier Coefficients

without ghost correction:

calcError(rec,odf,'L2')

ans =
    0.4926

with ghost correction:

calcError(rec_cor,odf,'L2')

ans =
    0.3400

Back to Top

Plot Fourier Coefficients

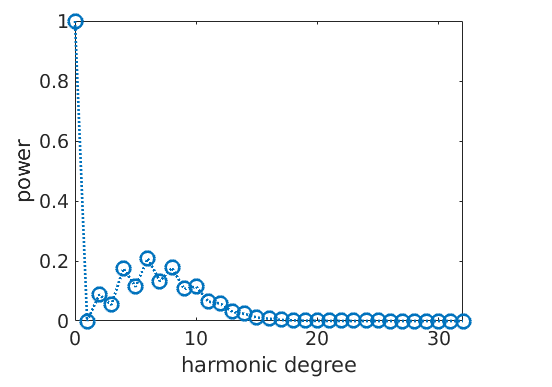
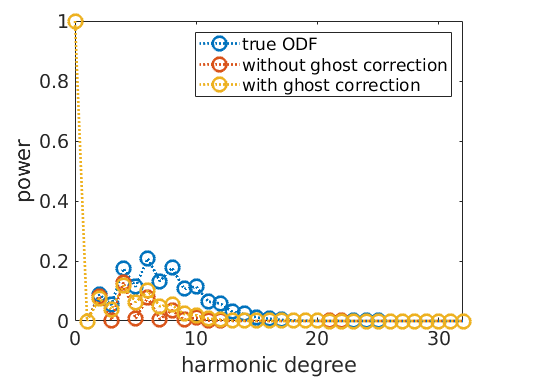
Plotting the Fourier coefficients of the recalculated ODFs shows that the Fourier coefficients without ghost correction oscillates much more than the Fourier coefficients with ghost correction

true ODF

close all;
plotFourier(odf,'linewidth',2)

keep plotting windows and add next plots

hold all

Without ghost correction:

plotFourier(rec,'linewidth',2)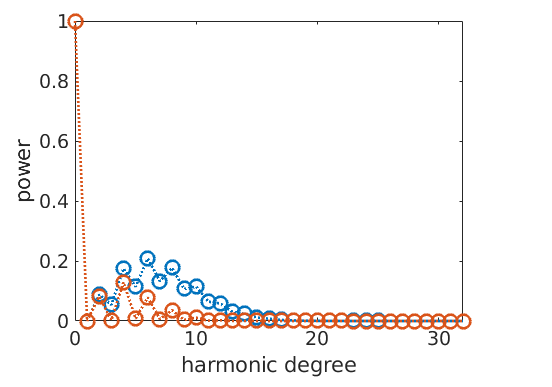

with ghost correction

plotFourier(rec_cor,'linewidth',2)
legend({'true ODF','without ghost correction','with ghost correction'})
% next plot command overwrites plot window
hold off

Back to Top

DocHelp 0.1 beta