Triple points
how to detect triple points
| On this page ... |
| Calculation of triple points |
| Index triple points by phase |
| Index triple points by grains |
| Index triple points by grain boundary |
| Boundary segments from triple points |
Calculation of triple points
MTEX automatically computes triple points during grain reconstruction. They are acessable similarly to grain boundaries as an property of the grain list.
% import some EBSD data set mtexdata small % compute grains grains = calcGrains(ebsd('indexed')); % extract all triple points tP = grains.triplePoints
tP = triplePointList
points mineral 1 mineral 2 mineral 3
15 Forsterite Forsterite Forsterite
7 Forsterite Forsterite Enstatite
4 Forsterite Enstatite Enstatite
8 Forsterite Forsterite Diopside
16 Forsterite Enstatite Diopside
4 Forsterite Diopside Diopside
2 Enstatite Enstatite Diopside
1 Enstatite Diopside Diopside
11 Diopside Diopside Diopside
Index triple points by phase
You may index triple points by the adjacent phases. The following command gives you all triple points with at least one phase being Forsterite
tP('Forsterite')
ans = triplePointList
points mineral 1 mineral 2 mineral 3
15 Forsterite Forsterite Forsterite
7 Forsterite Forsterite Enstatite
4 Forsterite Enstatite Enstatite
8 Forsterite Forsterite Diopside
16 Forsterite Enstatite Diopside
4 Forsterite Diopside Diopside
The following command gives you all triple points with at least two phases being Forsterite
tP('Forsterite','Forsterite')
ans = triplePointList
points mineral 1 mineral 2 mineral 3
15 Forsterite Forsterite Forsterite
7 Forsterite Forsterite Enstatite
8 Forsterite Forsterite Diopside
Finaly, we may mark all inner Diopside triple points
% smooth the grains a bit grains = smooth(grains,2); % and plot them plot(grains); % on top plot the triple points hold on plot(tP('Diopside','Diopside','Diopside'),'displayName','Di-Di-Di','color','b') hold off
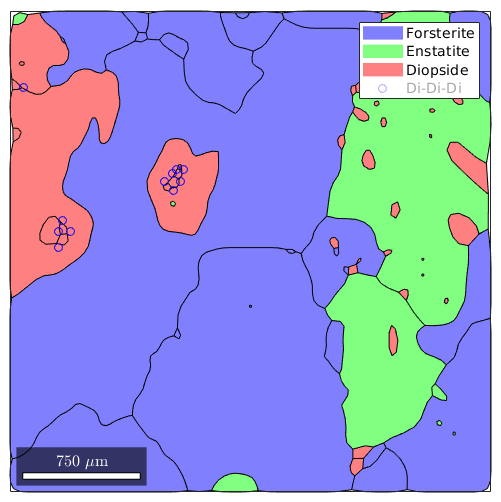
Index triple points by grains
Since, triple points are asociated to grains we may single out triple points that belong to a specific grain or some subset of grains.
% find the index of the largest grain [~,id] = max(grains.area); % the triple points that belong to the largest grain tP = grains(id).triplePoints; % plot these triple points plot(grains(id),'FaceColor',[0.2 0.8 0.8],'displayName','largest grains'); hold on plot(grains.boundary) plot(tP,'color','r') hold off
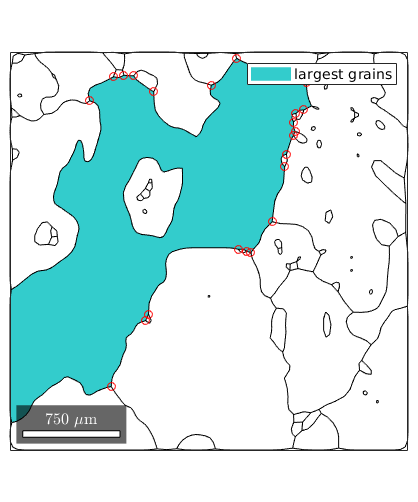
Index triple points by grain boundary
Triple points are not only a property of grains but also of grain boundaries. Thus we may ask for all triple points that belong to Fosterite - Forsterite boundaries with misorientation angle larger then 60 degree
% all Fosterite - Forsterite boundary segments gB_Fo = grains.boundary('Forsterite','Forsterite') % Fo - Fo segments with misorientation angle larger 60 degree gB_large = gB_Fo(gB_Fo.misorientation.angle>60*degree) % plot the triple points plot(grains) hold on plot(gB_large,'linewidth',2,'linecolor','w') plot(gB_large.triplePoints,'color','m') hold off
gB_Fo = grainBoundary
Segments mineral 1 mineral 2
255 Forsterite Forsterite
gB_large = grainBoundary
Segments mineral 1 mineral 2
55 Forsterite Forsterite
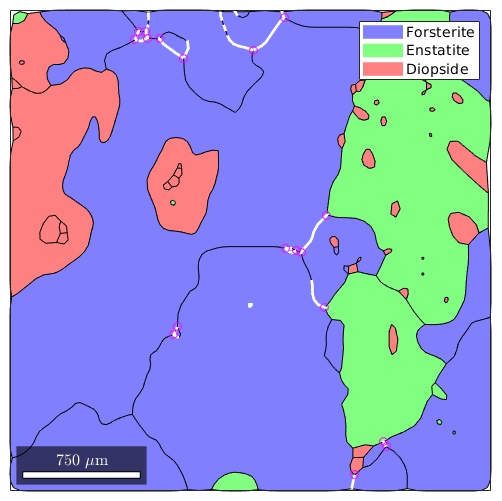
Boundary segments from triple points
On the other hand we may also ask for the boundary segments that build up a triple point. These are stored as the property boundaryId for each triple points.
% lets take Forsterite triple points tP = grains.triplePoints('Fo','Fo','Fo'); % the boundary segments which form the triple points gB = grains.boundary(tP.boundaryId); % plot the triple point boundary segments plot(grains) hold on plot(gB,'lineColor','w','linewidth',2) hold off
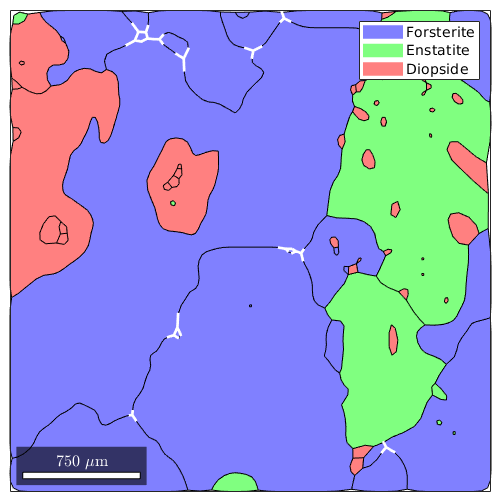
Once we have extracted the boundary segments adjecent to a triple point we may also extract the corresponding misorientations. The following command gives a n x 3 list of misorientations where n is the number of triple points
mori = gB.misorientation
mori = misorientation size: 15 x 3 crystal symmetry : Forsterite (mmm) crystal symmetry : Forsterite (mmm) antipodal: true
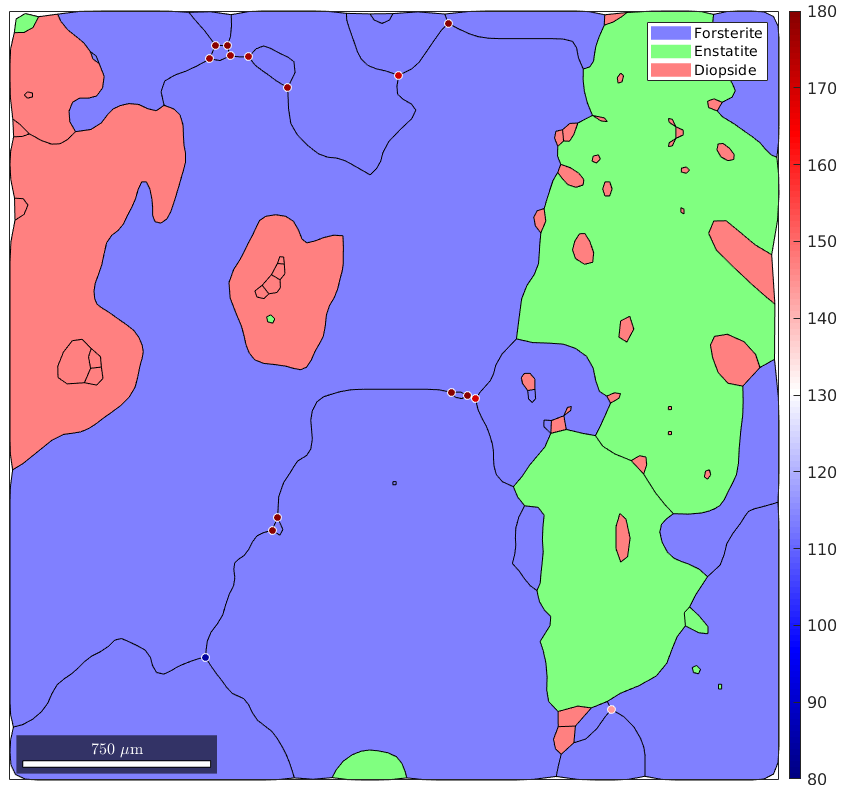
Hence, we can compute for each triple point the sum of misorientation angles by
sumMisAngle = sum(mori.angle,2);
and my visualize it by
plot(grains,'figSize','large') hold on plot(tP,sumMisAngle ./ degree,'markerEdgeColor','w') hold off mtexColorMap(blue2redColorMap) CLim(gcm,[80,180]) mtexColorbar
| DocHelp 0.1 beta |