Taylor Model
% display pole figure plots with RD on top and ND west plotx2north % store old annotation style storepfA = getMTEXpref('pfAnnotations'); % set new annotation style to display RD and ND pfAnnotations = @(varargin) text(-[vector3d.X,vector3d.Y],{'RD','ND'},... 'BackgroundColor','w','tag','axesLabels',varargin{:}); setMTEXpref('pfAnnotations',pfAnnotations);
Set up
consider cubic crystal symmetry
cs = crystalSymmetry('432'); % define a family of slip systems sS = slipSystem.bcc(cs); % some plane strain q = 0; epsilon = strainTensor(diag([1 -q -(1-q)])) % define a crystal orientation ori = orientation.byEuler(0,30*degree,15*degree,cs) % compute the Taylor factor [M,b,W] = calcTaylor(inv(ori)*epsilon,sS.symmetrise);
epsilon = strainTensor
rank: 2 (3 x 3)
1 0 0
0 0 0
0 0 -1
ori = orientation
size: 1 x 1
crystal symmetry : 432
specimen symmetry: 1
Bunge Euler angles in degree
phi1 Phi phi2 Inv.
0 30 15 0
The orientation dependence of the Taylor factor
The following code reproduces Fig. 5 of the paper of Bunge, H. J. (1970). Some applications of the Taylor theory of polycrystal plasticity. Kristall Und Technik, 5(1), 145-175. http://doi.org/10.1002/crat.19700050112
% set up an phi1 section plot sP = phi1Sections(cs,specimenSymmetry('222')); sP.phi1 = (0:10:90)*degree; % generate an orientations grid oriGrid = sP.makeGrid('resolution',2.5*degree); oriGrid.SS = specimenSymmetry; % compute Taylor factor for all orientations tic [M,~,W] = calcTaylor(inv(oriGrid)*epsilon,sS.symmetrise); toc % plot the taylor factor sP.plot(M,'smooth') mtexColorbar
computing Taylor factor: 100% Elapsed time is 15.844487 seconds.
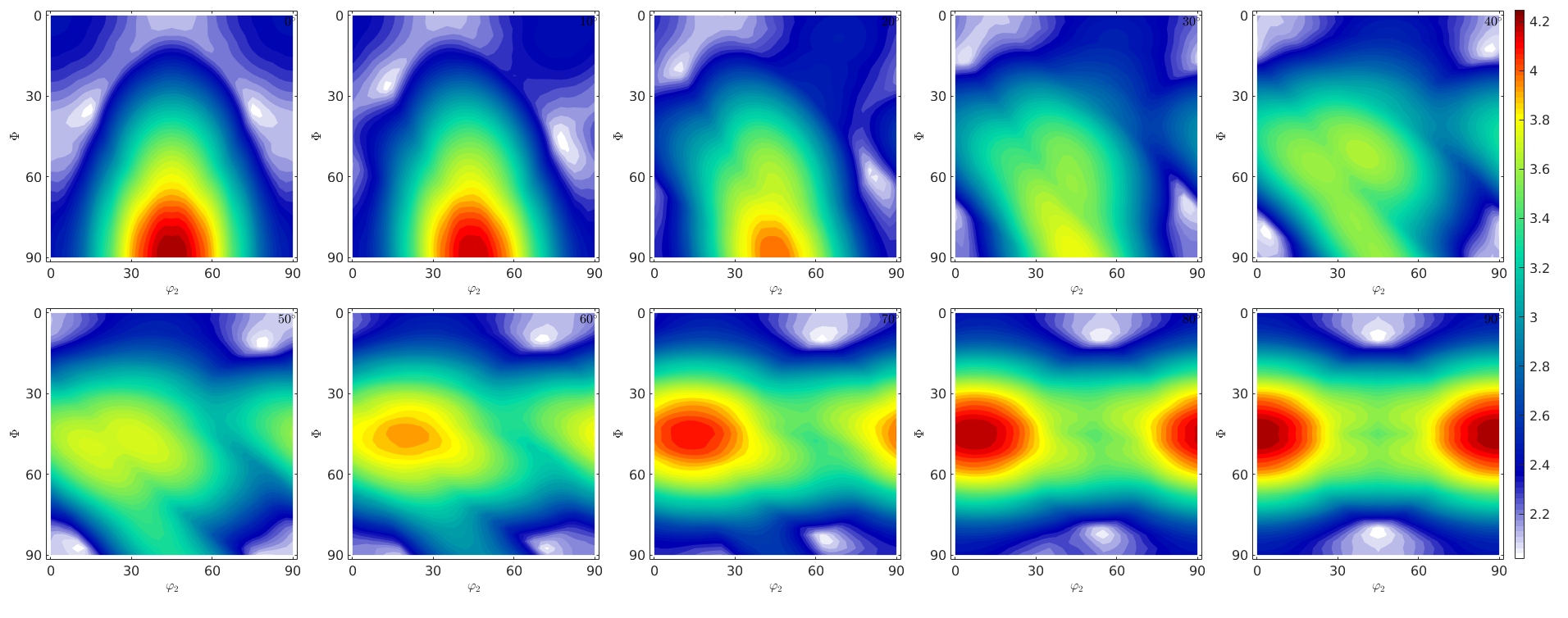
The orientation dependence of the spin
Compare Fig. 8 of the above paper
sP.plot(W.angle./degree,'smooth')
mtexColorbar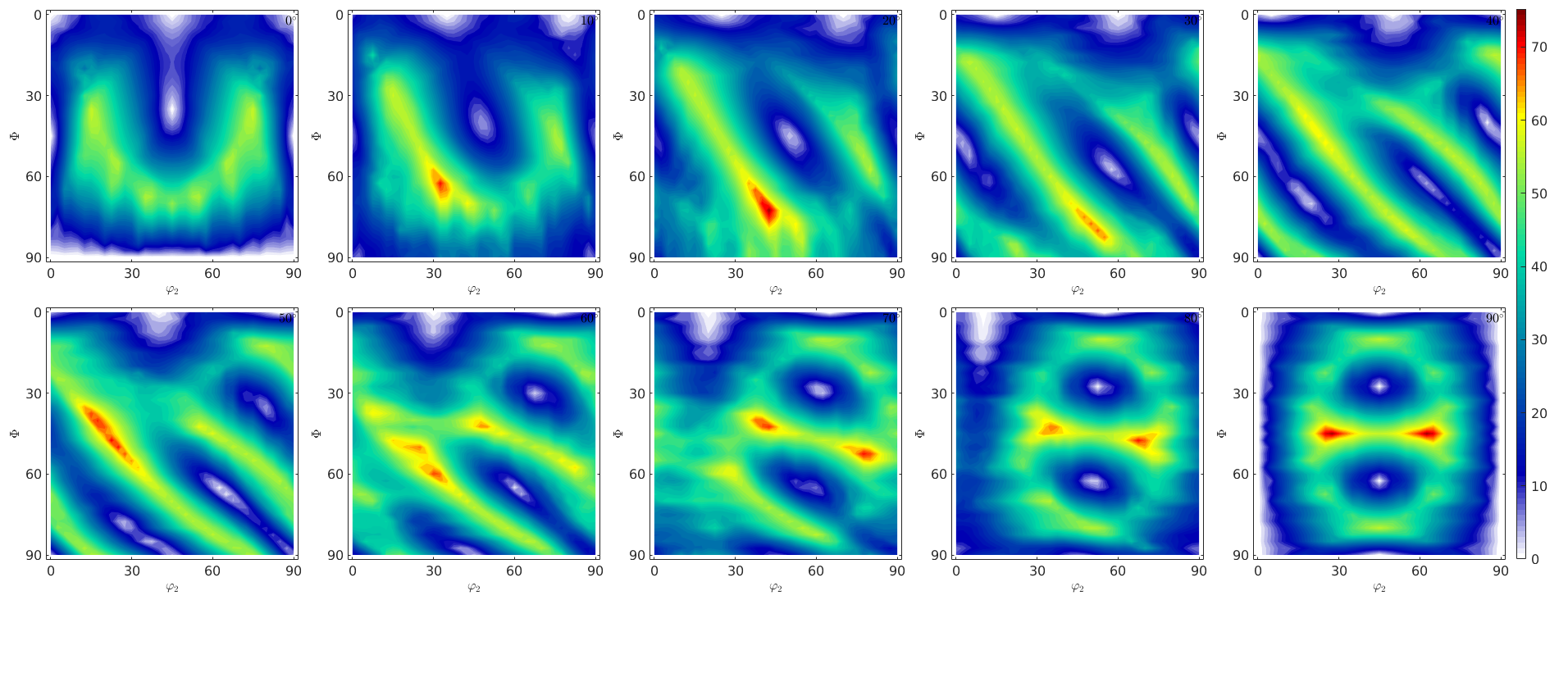
Display the crystallographic spin in sigma sections
sP = sigmaSections(cs,specimenSymmetry); oriGrid = sP.makeGrid('resolution',2.5*degree); [M,~,W] = calcTaylor(inv(oriGrid)*epsilon,sS.symmetrise); sP.plot(W.angle./degree,'smooth') mtexColorbar
computing Taylor factor: 100%
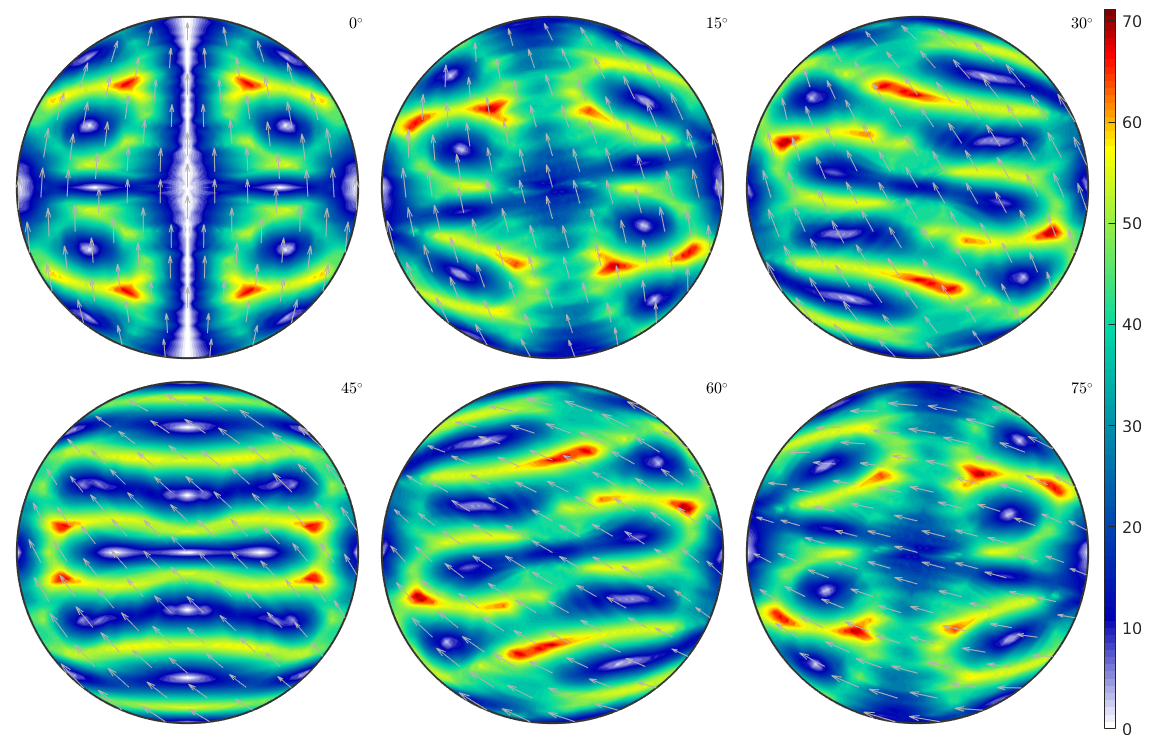
Most active slip direction
Next we consider a real world data set.
mtexdata csl % compute grains grains = calcGrains(ebsd('indexed')); grains = smooth(grains,5); % remove small grains grains(grains.grainSize <= 2) = []
grains = grain2d
Phase Grains Pixels Mineral Symmetry Crystal reference frame
-1 527 153693 iron m-3m
boundary segments: 21937
triple points: 1451
Properties: GOS, meanRotation
Next we apply the Taylor model to each grain of our data set
% some strain q = 0; epsilon = strainTensor(diag([1 -q -(1-q)])) % consider fcc slip systems sS = symmetrise(slipSystem.fcc(grains.CS)); % apply Taylor model [M,b,W] = calcTaylor(inv(grains.meanOrientation)*epsilon,sS);
epsilon = strainTensor rank: 2 (3 x 3) 1 0 0 0 0 0 0 0 -1 computing Taylor factor: 100%
% colorize grains according to Taylor factor plot(grains,M) mtexColorMap white2black mtexColorbar % index of the most active slip system - largest b [~,bMaxId] = max(b,[],2); % rotate the moste active slip system in specimen coordinates sSGrains = grains.meanOrientation .* sS(bMaxId); % visualize slip direction and slip plane for each grain hold on quiver(grains,sSGrains.b,'autoScaleFactor',0.5,'displayName','Burgers vector') hold on quiver(grains,sSGrains.trace,'autoScaleFactor',0.5,'displayName','slip plane trace') hold off
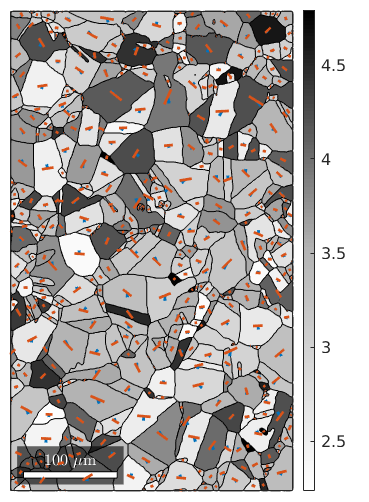
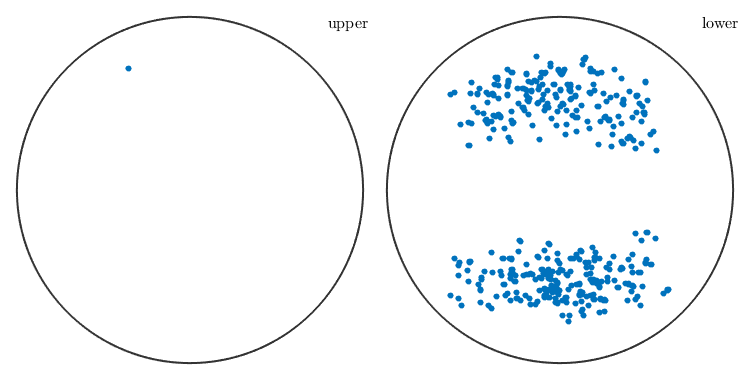
plot the most active slip directions observe that they point all towards the lower hemisphere - why? they do change if q is changed
figure(2) plot(sSGrains.b)
Texture evolution during rolling
% define some random orientations ori = orientation.rand(10000,cs); % 30 percent plane strain q = 0; epsilon = 0.3 * strainTensor(diag([1 -q -(1-q)])); % numIter = 10; progress(0,numIter); for sas=1:numIter % compute the Taylor factors and the orientation gradients [M,~,W] = calcTaylor(inv(ori) * epsilon ./ numIter, sS.symmetrise,'silent'); % rotate the individual orientations ori = ori .* orientation(-W); progress(sas,numIter); end
progress: 100%
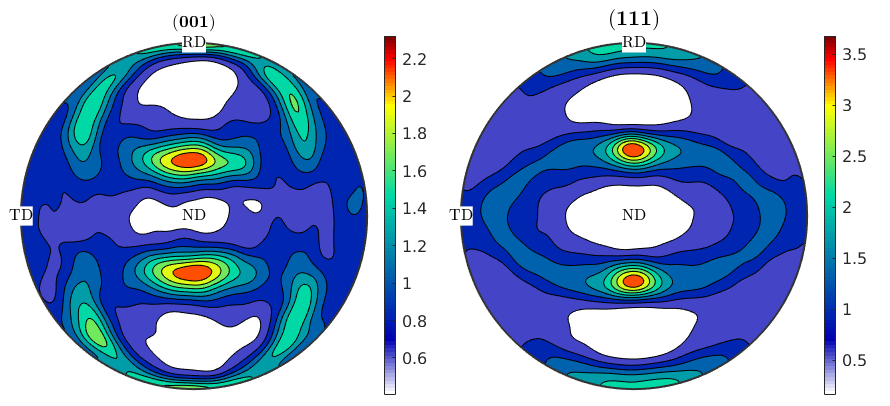
% plot the resulting pole figures % set new annotation style to display RD and ND pfAnnotations = @(varargin) text([vector3d.X,vector3d.Y,vector3d.Z],{'RD','TD','ND'},... 'BackgroundColor','w','tag','axesLabels',varargin{:}); setMTEXpref('pfAnnotations',pfAnnotations); plotPDF(ori,Miller({0,0,1},{1,1,1},cs),'contourf') mtexColorbar
restore MTEX preferences
setMTEXpref('pfAnnotations',storepfA);
Inverse Taylor
Use with care!
oS = axisAngleSections(cs,cs,'antipodal');
oS.angles = 10*degree;
ori = oS.makeGrid;
[M,b,eps] = calcInvTaylor(ori,sS.symmetrise);computing Taylor factor: 100%
plot(oS,M,'contourf')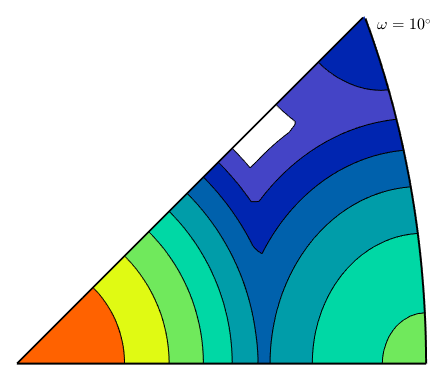
| DocHelp 0.1 beta |