S2VectorFieldHarmonic
S2VectorField handles three-dimensional functions on the sphere. For instance the gradient of an univariate S2FunHarmonic can return a S2VectorFieldHarmonic.
| On this page ... |
| Defining a S2VectorFieldHarmonic |
| Operations |
| Visualization |
| Complete Function list |
Defining a S2VectorFieldHarmonic
Definition via function values
At first you need some vertices
nodes = equispacedS2Grid('points', 1e5);
nodes = nodes(:);Next you define function values for the vertices
y = vector3d.byPolar(sin(3*nodes.theta), nodes.rho+pi/2);
Now the actual command to get sVF1 of type S2VectorFieldHarmonic
sVF1 = S2VectorFieldHarmonic.approximation(nodes, y)
sVF1 = S2VectorFieldHarmonic bandwidth: 128
Definition via function handle
If you have a function handle for the function you could create a S2VectorFieldHarmonic via quadrature. At first lets define a function handle which takes vector3d as an argument and returns also vector3d:
f = @(v) vector3d(v.x, v.y, 0*v.x);
Now you can call the quadrature command to get sVF2 of type S2VectorFieldHarmonic
sVF2 = S2VectorFieldHarmonic.quadrature(@(v) f(v))
sVF2 = S2VectorFieldHarmonic bandwidth: 128
Definition via S2FunHarmonic
If you directly call the constructor with a multivariate S2FunHarmonic sF with two or three entries it will create a S2VectorFieldHarmonic with sF(1) the polar angle and sF(2) the azimuth or sF(1), sF(2) and sF(3) the  and
and  component.
component.
sF = S2FunHarmonic(rand(10, 2)); sVF3 = S2VectorFieldHarmonic(sF) sF = S2FunHarmonic(rand(10, 3)); sVF4 = S2VectorFieldHarmonic(sF)
sVF3 = S2VectorFieldHarmonic bandwidth: 3 sVF4 = S2VectorFieldHarmonic bandwidth: 3
Operations
Basic arithmetic operations
addition/subtraction
sVF1+sVF2; sVF1+vector3d(1, 0, 0); sVF1-sVF2; sVF2-vector3d(sqrt(2)/2, sqrt(2)/2, 0);
multiplication/division
2.*sVF1; sVF1./4;
dot product
dot(sVF1, sVF2); dot(sVF1, vector3d(0, 0, 1));
cross product
cross(sVF1, sVF2); cross(sVF1, vector3d(0, 0, 1));
Other operations
mean value
mean(sVF1);
Rotation
r = rotation.byEuler( [pi/4 0 0]); rotate(sVF1, r);
pointwise norm of the vectors
norm(sVF1);
Visualization
the default plot-command
plot(sVF1);
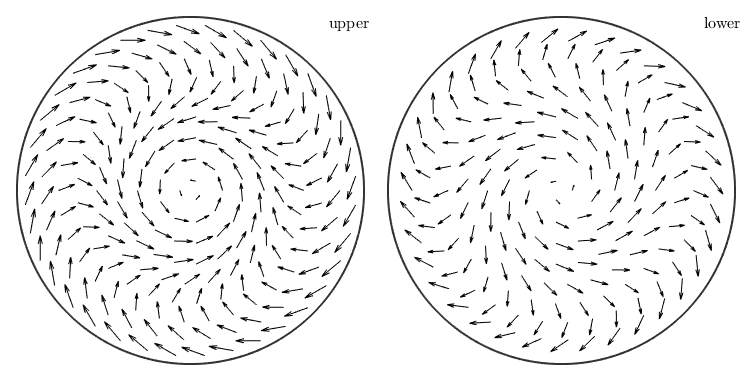
- same as quiver(sVF1)
3D plot of a sphere with the vectors on itself
clf; quiver3(sVF2);
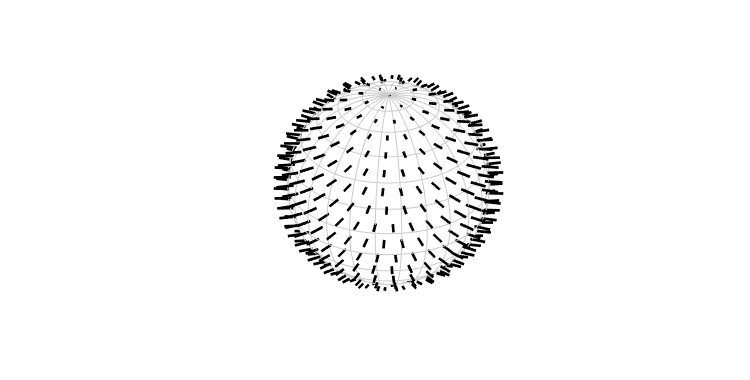
Complete Function list
| DocHelp 0.1 beta |