Plotting grains
how to colorize grains
| On this page ... |
| Phase maps |
| Orientation Maps |
| Plotting arbitrary properties |
| Colorizing circular properties |
| Plotting the orientation within a grain |
| Visualizing directions |
| Labeling Grains |
We start by importing some EBSD data and reconstructing some grains
% import a demo data set mtexdata forsterite plotx2east % consider only indexed data for grain segmentation ebsd = ebsd('indexed'); % perform grain segmentation [grains,ebsd.grainId,ebsd.mis2mean] = calcGrains(ebsd);
Phase maps
When using the plot command without additional argument the associated color is defined by color stored in the crystal symmetry for each phase
close all plot(grains) grains('Fo').CS.color
ans =
'light blue'
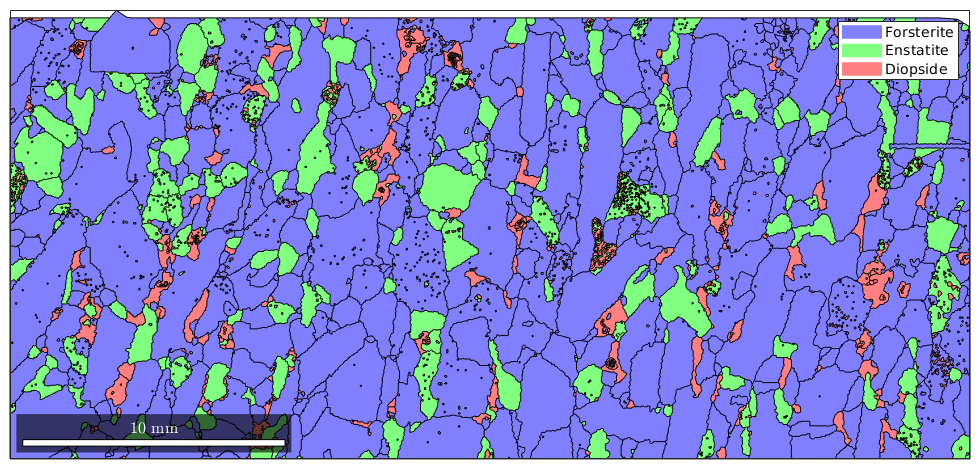
Accodingly, changing the color stored in the crystal symmetry changes the color in the map
grains('Fo').CS.color = 'yellow' plot(grains)
grains = grain2d
Phase Grains Pixels Mineral Symmetry Crystal reference frame
1 1080 152345 Forsterite mmm
2 515 26058 Enstatite mmm
3 1496 9064 Diopside 12/m1 X||a*, Y||b*, Z||c
boundary segments: 43912
triple points: 3417
Properties: GOS, meanRotation

The color can also been specified directly by using the option FaceColor. Note, that this requires the color to be specified by RGB values.
% detect the largest grain [~,id] = max(grains.area); % plot the grain in black with some transperency hold on plot(grains(id),'FaceColor',[0 0 0],'FaceAlpha',0.35) hold off

Orientation Maps
Coloring grains according to their mean orientations is very similar to EBSD maps colored by orientations. The most important thing is that the misorientation can only extracte from grains of the same phase.
% the implicite way plot(grains('Fo'),grains('fo').meanOrientation)
I'm going to colorize the orientation data with the standard MTEX colorkey. To view the colorkey do: colorKey = ipfColorKey(ori_variable_name) plot(colorKey)

This implicte way gives no control about how the color is computed from the meanorientation. When using the explicite way by defining a orientation to color map
% this defines a ipf color key ipfKey = ipfColorKey(grains('Fo'));
we can set the inverse pole figure direction and many other properties
ipfKey.inversePoleFigureDirection = xvector; % compute the colors from the meanorientations color = ipfKey.orientation2color(grains('Fo').meanOrientation); % and use them for plotting plot(grains('fo'),color)

Plotting arbitrary properties
As we have seen in the previous section the plot command accepts as second argument any list of RGB values specifying a color. Instead of RGB values the second argument can also be a list of values which are then transformed by a colormap into color.
As an example we colorize the grains according to their aspect ratio.
plot(grains,grains.aspectRatio)

we see that we have a very alongated grain which makes it difficult to distinguesh the aspect ration of the other grains. A solution for this is to specify the values of the aspect ration which should maped to the top and bottom color of the colormap
CLim(gcm,[1 5])

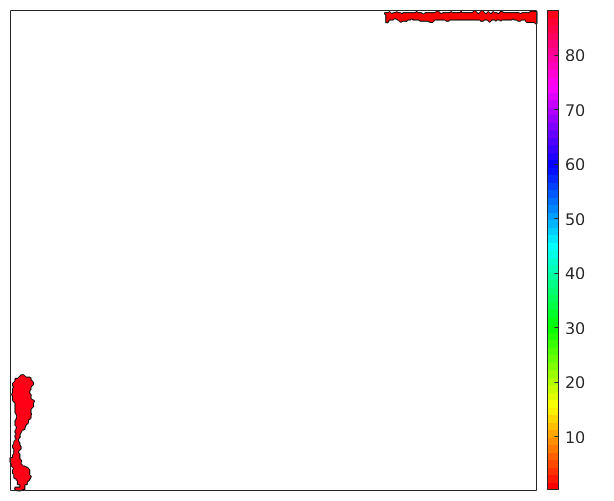
Colorizing circular properties
Sometimes the property we want to display is a circular, e.g., the direction of the grain alongation. In this case it is important to use a circular colormap which assign the same color to high values and low values. In the case of the direction of the grain alongation the angles 0 and 180 should get the same color since they represent the same direction.
% consider only alongated grains alongated_grains = grains(grains.aspectRatio > 5); % get the grain alongation dir = alongated_grains.principalComponents; % transfer this into degree and project it into the interval [0,180] dir = mod(dir./degree,180); % plot the direction plot(alongated_grains,dir,'micronbar','off') % change the default colormap to a circular one mtexColorMap HSV % display the colormap mtexColorbar
Plotting the orientation within a grain
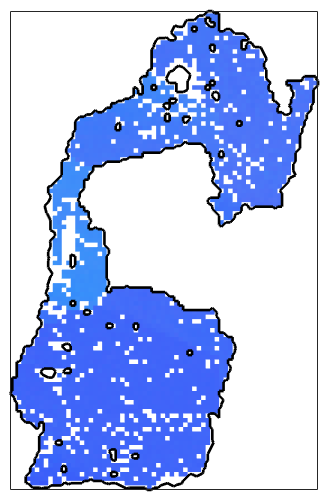
In order to plot the orientations of EBSD data within certain grains one first has to extract the EBSD data that belong to the specific grains.
% let have a look at the bigest grain [~,id] = max(grains.area) % and select the corresponding EBSD data ebsd_maxGrain = ebsd(ebsd.grainId == id) % the previous command is equivalent to the more simpler ebsd_maxGrain = ebsd(grains(id));
id =
931
ebsd_maxGrain = EBSD
Phase Orientations Mineral Color Symmetry Crystal reference frame
1 2683 (100%) Forsterite light blue mmm
Properties: bands, bc, bs, error, mad, x, y, grainId, mis2mean
Scan unit : um
% compute the color out of the orientations color = ipfKey.orientation2color(ebsd_maxGrain.orientations); % plot it plot(ebsd_maxGrain, color,'micronbar','off') % plot the grain boundary on top hold on plot(grains(id).boundary,'linewidth',2) hold off
Visualizing directions
We may also visualize directions by arrows placed at the center of the grains.
% load some single phase data set mtexdata csl % compute and plot grains [grains,ebsd.grainId] = calcGrains(ebsd); plot(grains,grains.meanOrientation,'micronbar','off','figSize','large') % next we want to visualize the direction of the 100 axis dir = grains.meanOrientation * Miller(1,0,0,grains.CS); % the lenght of the vectors should depend on the grain diameter len = 0.25*grains.diameter; % arrows are plotted using the command quiver. We need to switch of auto % scaling of the arrow length hold on quiver(grains,len.*dir,'autoScale','off','color','black') hold off
I'm going to colorize the orientation data with the standard MTEX colorkey. To view the colorkey do: colorKey = ipfColorKey(ori_variable_name) plot(colorKey)

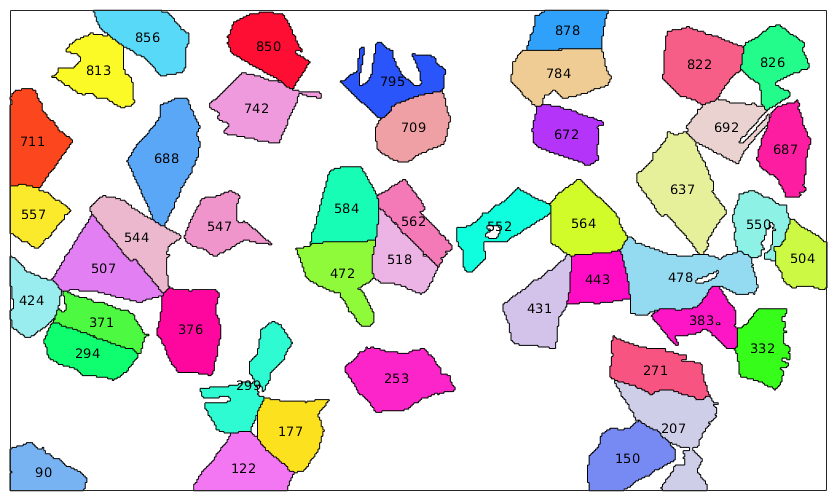
Labeling Grains
In the above example the vectors are centered at the centroids of the grains. Other elements
% only the very big grains big_grains = grains(grains.grainSize>1000); % plot them plot(big_grains,big_grains.meanOrientation,'micronbar','off') % plot on top their ids text(big_grains,int2str(big_grains.id))
I'm going to colorize the orientation data with the standard MTEX colorkey. To view the colorkey do: colorKey = ipfColorKey(ori_variable_name) plot(colorKey)
| DocHelp 0.1 beta |