Bingham distribution and EBSD data
testing rotational symmetry of individual orientations
| On this page ... |
| Bingham Distribution |
| The bipolar case and unimodal distribution |
| Prolate case and fibre distribution |
| Oblate case |
Bingham Distribution
The quaternionic Bingham distribution has the density
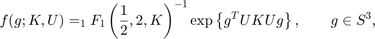
where 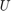 are an
are an 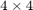 orthogonal matrix with unit quaternions
orthogonal matrix with unit quaternions 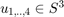 in the column and
in the column and 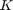 a
a 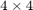 diagonal matrix with the entries
diagonal matrix with the entries 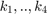 describing the shape of the distribution.
describing the shape of the distribution. 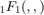 is the hypergeometric function with matrix argument normalizing the density.
is the hypergeometric function with matrix argument normalizing the density.
The shape parameters 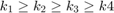 give
give
- a bipolar distribution, if
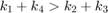 ,
,
- a circular distribution, if
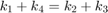 ,
,
- a spherical distribution, if
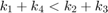 ,
,
- a uniform distribution, if
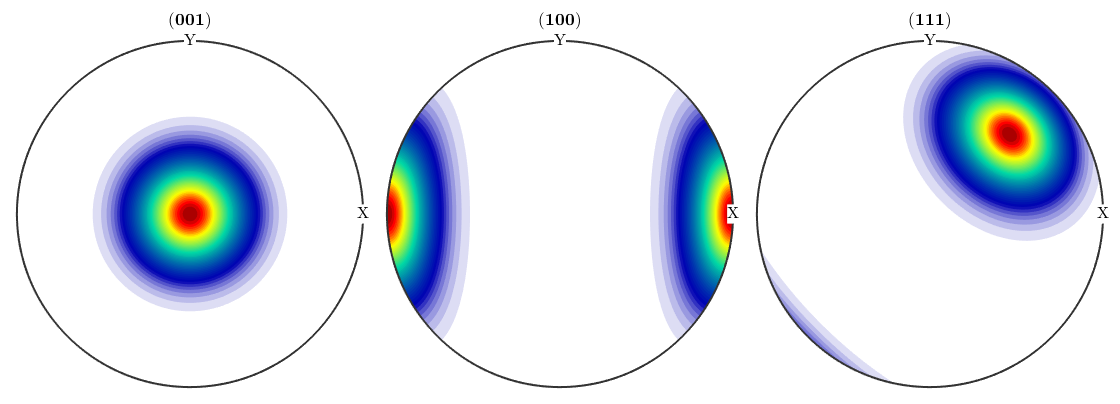
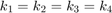 ,
,
in unit quaternion space. Since the quaternion +g and -g describes the same rotation, the bipolar distribution corresponds to an unimodal distribution in orientation space. Moreover, we would call the circular distribution a fibre in orientation space.
The general setup of the Bingham distribution in MTEX is done as follows
cs = crystalSymmetry('1'); kappa = [100 90 80 0]; % shape parameters U = eye(4); % orthogonal matrix odf = BinghamODF(kappa,U,cs)
odf = ODF
crystal symmetry : 1, X||a, Y||b*, Z||c*
specimen symmetry: 1
Bingham portion:
kappa: 100 90 80 0
weight: 1
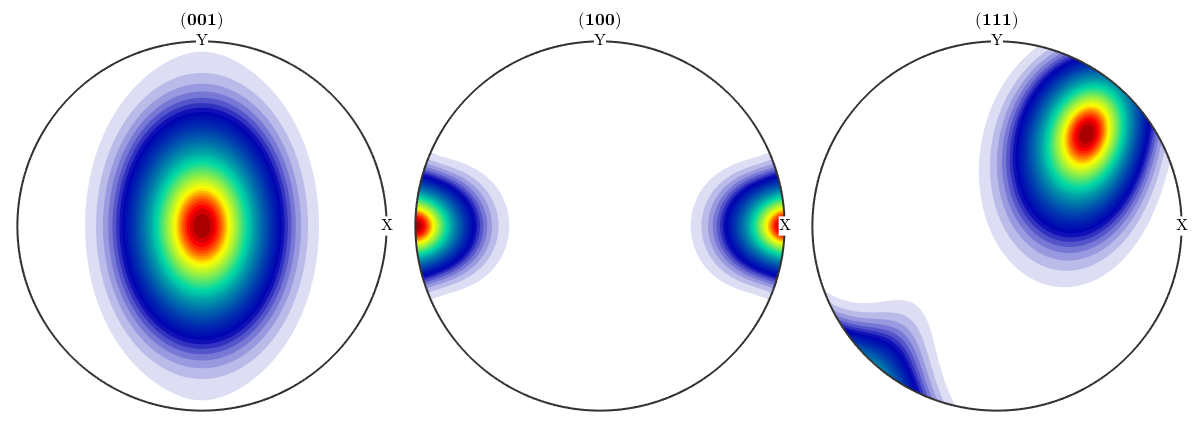
h = [Miller(0,0,1,cs) Miller(1,0,0,cs) Miller(1,1,1,cs)]; plotPDF(odf,h,'antipodal','silent'); % plot(odf,'sections',10)
The bipolar case and unimodal distribution
First, we define some unimodal odf
odf_spherical = unimodalODF(orientation.id(cs),'halfwidth',20*degree)
odf_spherical = ODF
crystal symmetry : 1, X||a, Y||b*, Z||c*
specimen symmetry: 1
Radially symmetric portion:
kernel: de la Vallee Poussin, halfwidth 20°
center: (0°,0°,0°)
weight: 1
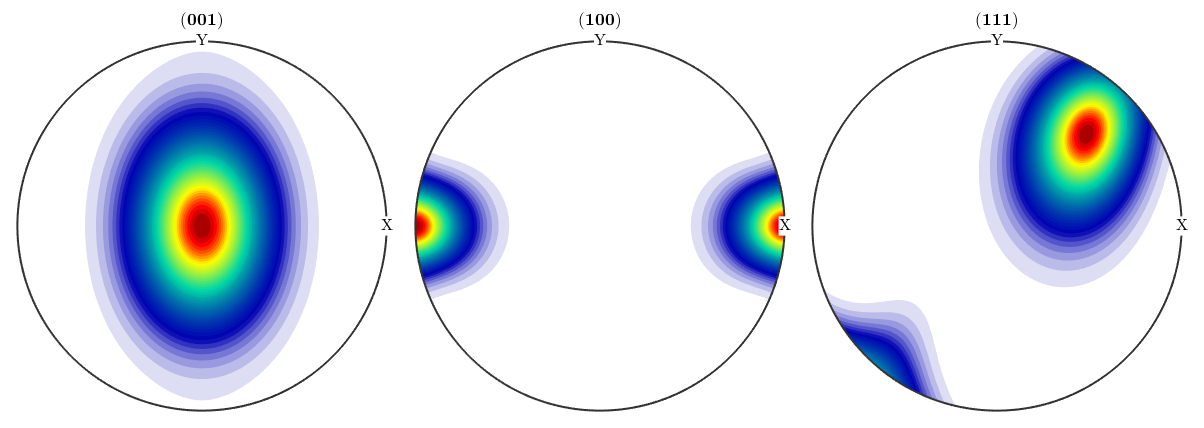
plotPDF(odf_spherical,h,'antipodal','silent')
Next, we simulate individual orientations from this odf, in a scattered axis/angle plot in which the simulated data looks like a sphere
ori_spherical = calcOrientations(odf_spherical,1000);
close all
scatter(ori_spherical)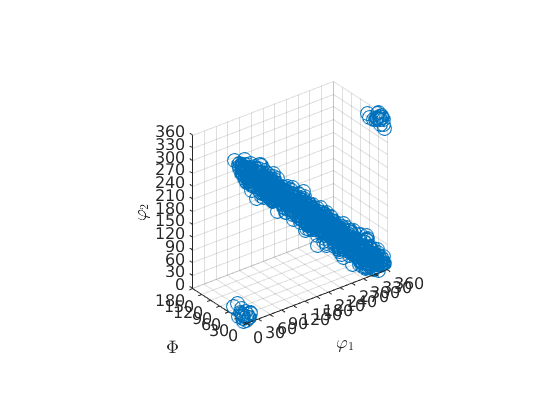
From this simulated EBSD data, we can estimate the parameters of the Bingham distribution,
calcBinghamODF(ori_spherical)
ans = ODF
crystal symmetry : 1, X||a, Y||b*, Z||c*
specimen symmetry: 1
Bingham portion:
kappa: 0 0.82596 2.8101 26.7107
weight: 1
where U is the orthogonal matrix of eigenvectors of the orientation tensor and kappa the shape parameters associated with the U.
next, we test the different cases of the distribution on rejection
T_spherical = bingham_test(ori_spherical,'spherical','approximated'); T_oblate = bingham_test(ori_spherical,'prolate', 'approximated'); T_prolate = bingham_test(ori_spherical,'oblate', 'approximated'); t = [T_spherical T_oblate T_prolate]
t =
0.3441 0.1160 0.5486
The spherical test case failed to reject it for some level of significance, hence we would dismiss the hypothesis prolate and oblate.
odf_spherical = BinghamODF(kappa,U,crystalSymmetry,specimenSymmetry)
odf_spherical = ODF
crystal symmetry : 1, X||a, Y||b*, Z||c*
specimen symmetry: 1
Bingham portion:
kappa: 100 90 80 0
weight: 1
plotPDF(odf_spherical,h,'antipodal','silent')
Prolate case and fibre distribution
The prolate case correspondes to a fibre.
odf_prolate = fibreODF(Miller(0,0,1,crystalSymmetry('1')),zvector,... 'halfwidth',20*degree)
odf_prolate = ODF
crystal symmetry : 1, X||a, Y||b*, Z||c*
specimen symmetry: 1
Fibre symmetric portion:
kernel: de la Vallee Poussin, halfwidth 20°
fibre: (001) - 0,0,1
weight: 1
plotPDF(odf_prolate,h,'upper','silent')
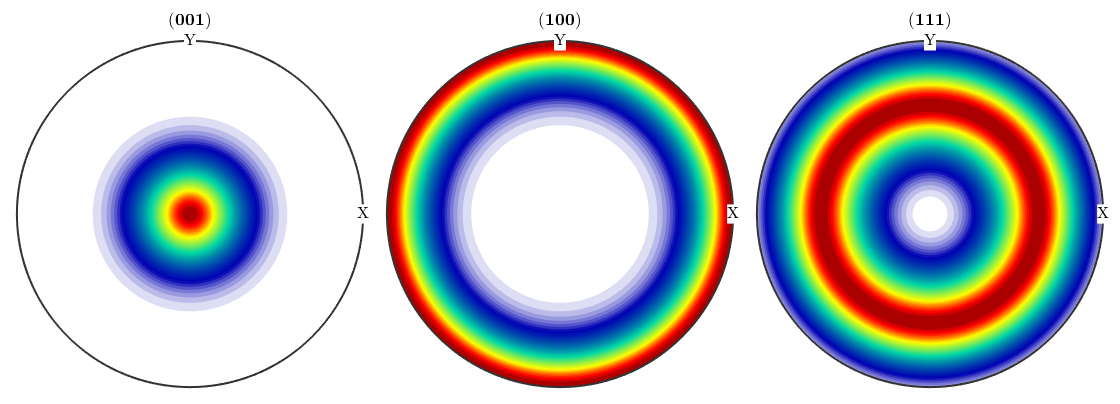
As before, we generate some random orientations from a model odf. The shape in an axis/angle scatter plot reminds of a cigar
ori_prolate = calcOrientations(odf_prolate,1000);
close all
scatter(ori_prolate)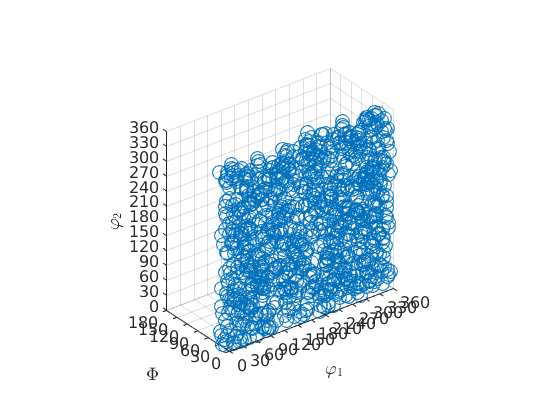
We estimate the parameters of the Bingham distribution
calcBinghamODF(ori_prolate)
ans = ODF
crystal symmetry : 1, X||a, Y||b*, Z||c*
specimen symmetry: 1
Bingham portion:
kappa: 0 2.2873 51.2566 52.282
weight: 1
and test on the three cases
T_spherical = bingham_test(ori_prolate,'spherical','approximated'); T_oblate = bingham_test(ori_prolate,'prolate', 'approximated'); T_prolate = bingham_test(ori_prolate,'oblate', 'approximated'); t = [T_spherical T_oblate T_prolate]
t =
1.0000 0.2213 1.0000
The test clearly rejects the spherical and prolate case, but not the prolate. We construct the Bingham distribution from the parameters, it might show some skewness
odf_prolate = BinghamODF(kappa,U,crystalSymmetry,specimenSymmetry)
odf_prolate = ODF
crystal symmetry : 1, X||a, Y||b*, Z||c*
specimen symmetry: 1
Bingham portion:
kappa: 100 90 80 0
weight: 1
plotPDF(odf_prolate,h,'antipodal','silent')
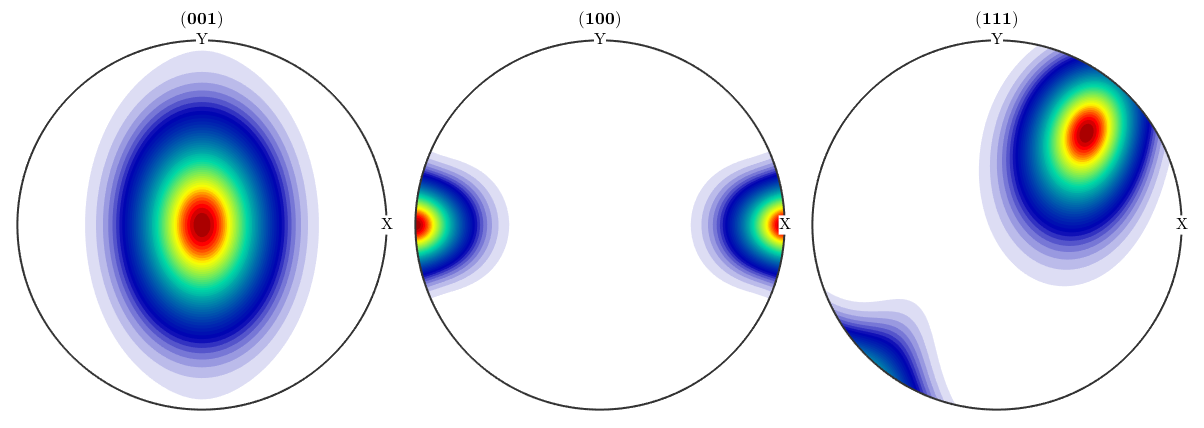
Oblate case
The oblate case of the Bingham distribution has no direct counterpart in terms of texture components, thus we can construct it straightforward
odf_oblate = BinghamODF([50 50 50 0],eye(4),crystalSymmetry,specimenSymmetry)
odf_oblate = ODF
crystal symmetry : 1, X||a, Y||b*, Z||c*
specimen symmetry: 1
Bingham portion:
kappa: 50 50 50 0
weight: 1
plotPDF(odf_oblate,h,'antipodal','silent')
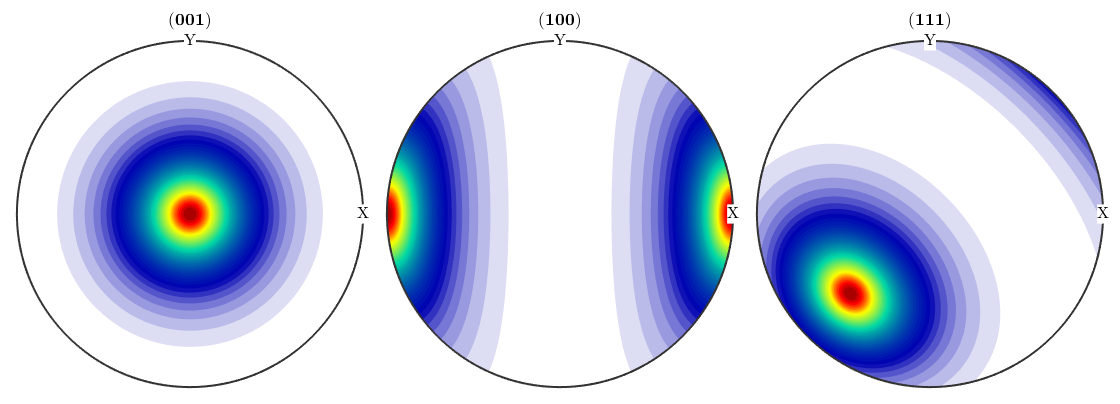
The oblate cases in axis/angle space remind on a disk
ori_oblate = calcOrientations(odf_oblate,1000);
close all
scatter(ori_oblate)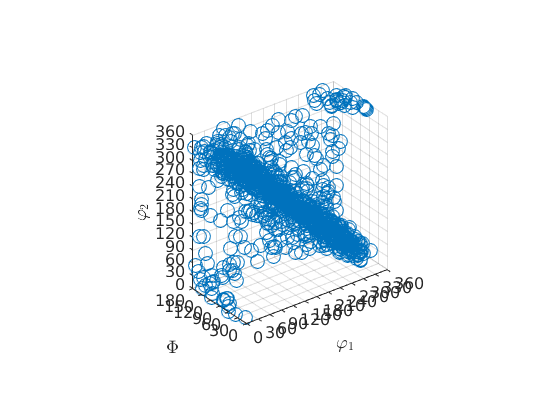
We estimate the parameters again
calcBinghamODF(ori_oblate)
ans = ODF
crystal symmetry : 1, X||a, Y||b*, Z||c*
specimen symmetry: 1
Bingham portion:
kappa: 0 45.8815 45.9351 47.454
weight: 1
and do the tests
T_spherical = bingham_test(ori_oblate,'spherical','approximated'); T_oblate = bingham_test(ori_oblate,'prolate', 'approximated'); T_prolate = bingham_test(ori_oblate,'oblate', 'approximated'); t = [T_spherical T_oblate T_prolate]
t =
1.0000 1.0000 0.1396
the spherical and oblate case are clearly rejected, the prolate case failed to reject for some level of significance
odf_oblate = BinghamODF(kappa, U,crystalSymmetry,specimenSymmetry)
odf_oblate = ODF
crystal symmetry : 1, X||a, Y||b*, Z||c*
specimen symmetry: 1
Bingham portion:
kappa: 100 90 80 0
weight: 1
plotPDF(odf_oblate,h,'antipodal','silent')
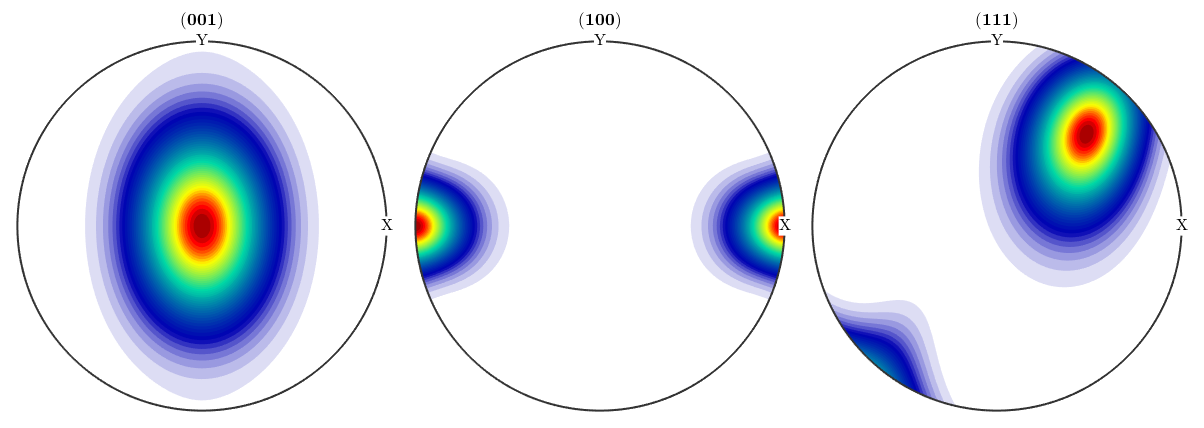
| DocHelp 0.1 beta |